resume cover letter a

How to Write a Cover Letter: Your Full Guide (With Tips and Examples)

It’s a familiar cycle: You sit down to write a cover letter, open a blank document, check your email, browse cover letter examples , do some chores, watch that cursor blink a few more times, and finally Google something like “how to write a cover letter”—which hopefully brought you here. But you still might be thinking, does anyone really read cover letters? Why do they even exist?

First: Yes, we can assure you that cover letters do, in fact, get read. To some hiring managers, they’re the most important part of your job application. And regardless, you don’t want to miss the opportunity to tell prospective employers who you are, showcase why they should hire you, and stand out above all the other candidates.

To ensure your letter is in amazing shape (and crafting it is as painless as possible), we’ve got easy-to-follow steps plus examples, a few bonus tips, and answers to frequently asked questions.

Get that cover letter out there! Browse open jobs on The Muse and find your dream job »

What is a cover letter and why is it important?

A cover letter is a brief (one page or less) note that you write to a hiring manager or recruiter to go along with your resume and other application materials.

Done well, a cover letter gives you the chance to speak directly to how your skills and experience line up with the specific job you’re pursuing. It also affords you an opportunity to hint to the reviewer that you’re likable, original, and likely to be a great addition to the team.

Instead of using cover letters to their strategic advantage, most job applicants blabber on and on about what they want, toss out bland, cliché-filled paragraphs that essentially just regurgitate their resume, or go off on some strange tangent in an effort to be unique. Given this reality, imagine the leg up you’ll have once you learn how to do cover letters right.

How long should a cover letter be?

An ideal cover letter typically ranges from a half page to one full page. Aim to structure it into four paragraphs, totaling around 250 to 400 words, unless the job posting states otherwise. Some employers may have specific guidelines like word or character limits, writing prompt, or questions to address. In such cases, be sure to follow these instructions from the job posting.

How to write a cover letter hiring managers will love

Now that you’re sold on how important cover letters are, here are eight steps to writing one that screams, “I’m a great hire!”

Step 1: Write a fresh cover letter for each job (but yes, you can use a template)

Sure, it’s way faster and easier to take the cover letter you wrote for your last application, change the name of the company, and send it off. But most employers want to see that you’re truly excited about the specific position and organization—which means creating a custom letter for each position.

While it’s OK to recycle a few strong sentences and phrases from one cover letter to the next, don’t even think about sending out a 100% generic letter. “Dear Hiring Manager, I am excited to apply to the open position at your company” is an immediate signal to recruiters and hiring managers that you’re mass-applying to every job listing that pops up on LinkedIn.

At the same time, there’s nothing that says you can’t get a little help: Try out one of our free cover letter templates to make the process a bit easier.

Step 2: Add your contact info

At the top of your cover letter, you should list out your basic info. You can even copy the same heading from your resume if you’d like. Some contact info you might include (and the order to include it in):

• Your pronouns (optional)
• Your location (optional)
• Your email address
• Your phone number (optional)
• Your Linkedin, portfolio, or personal website URL (optional)

Note that only name and email are mandatory, and you don’t need to put a full address on a cover letter or resume anymore. A city and state (or metro area) are more than enough. So your header might look like this:

Inigo Montoya he/him Florin Metropolitan Area [email protected] 555-999-2222

If the job posting tells you to submit your cover letter in the body of an email, you can add your contact info at the end, after your name (and if you’d like to forgo the email address here, you can—they have it already). So your sign off could look like this:

Violet Baudelaire she/her [email protected] 123-123-1234

https://www.linkedin.com/in/violet-baudelaire/

Step 3: Address your cover letter to the hiring manager—preferably by name

The most traditional way to address a cover letter is to use the person’s first and last name, including “Mr.” or “Ms.” (for example, “Dear Ms. Jane Smith” or just “Dear Ms. Smith”). But to avoid accidentally using the wrong title—or worse, inadvertently misgendering someone—first and last name also work just fine.

If “Dear” feels a bit too stiff, try “Hello.” But never use generic salutations like “ To Whom it May Concern ” or “Dear Sir or Madam.”

For more help, read these rules for addressing your cover letter and a few tips for how to find the hiring manager .

Step 4: Craft an opening paragraph that’ll hook your reader

Your opening sets the stage for the whole cover letter. So you want it to be memorable, friendly, conversational, and hyper-relevant to the job you’re pursuing.

No need to lead with your name—the hiring manager can see it already. But it’s good to mention the job you’re applying for (they may be combing through candidates for half a dozen different jobs).

You could go with something simple like, “I am excited to apply for [job] with [Company].” But consider introducing yourself with a snappy first paragraph that highlights your excitement about the company you’re applying to, your passion for the work you do, and/or your past accomplishments.

This is a prime spot to include the “why” for your application. Make it very clear why you want this job at this company. Are you a longtime user of their products? Do you have experience solving a problem they’re working on? Do you love their brand voice or approach to product development? Do your research on the company (and check out their Muse profile if they have one) to find out.

Read this next: 30 Genius Cover Letter Openers Recruiters Will LOVE

Step 5: Convey why you’d be a great hire for this job

A common cover letter mistake is only talking about how great the position would be for you. Frankly, hiring managers are aware of that—what they really want to know is what you’re going to bring to the position and company.

So once you’ve got the opening under wraps, you should pull out a few key ideas that will make up the backbone of your cover letter. They should show that you understand what the organization is looking for and spell out how your background lines up with the position.

Study the job description for hints . What problems is the company looking to solve with this hire? What skills or experiences are mentioned high up, or more than once? These will likely be the most important qualifications.

If you tend to have a hard time singing your own praises and can’t nail down your strengths , here’s a quick trick: What would your favorite boss, your best friend, or your mentor say about you? How would they sing your praises? Use the answers to inform how you write about yourself. You can even weave in feedback you’ve received to strengthen your case (occasionally, don’t overuse this!). For example:

“When I oversaw our last office move, my color-coded spreadsheets covering every minute detail of the logistics were legendary; my manager said I was so organized, she’d trust me to plan an expedition to Mars.”

Step 6: Back up your qualifications with examples and numbers

Look at your list of qualifications from the previous step, and think of examples from your past that prove you have them. Go beyond your resume. Don’t just regurgitate what the hiring manager can read elsewhere.

Simply put, you want to paint a fuller picture of what experiences and accomplishments make you a great hire and show off what you can sashay through their doors with and deliver once you land the job.

For example, what tells a hiring manager more about your ability to win back former clients? This: “I was in charge of identifying and re-engaging former clients.” Or this: “By analyzing past client surveys, NPS scores, and KPIs, as well as simply picking up the phone, I was able to bring both a data-driven approach and a human touch to the task of re-engaging former clients.”

If you're having trouble figuring out how to do this, try asking yourself these questions and finding answers that line up with the qualifications you’ve chosen to focus on:

• What approach did you take to tackling one of the responsibilities you’ve mentioned on your resume?
• What details would you include if you were telling someone a (very short!) story about how you accomplished one of your resume bullet points?
• What about your personality, passion, or work ethic made you especially good at getting the job done?

Come up with your examples, then throw in a few numbers. Hiring managers love to see stats—they show you’ve had a measurable impact on an organization you’ve worked for. Did you bring in more clients than any of your peers? Put together an impressive number of events? Make a process at work 30% more efficient? Work it into your cover letter!

This might help: How to Quantify Your Resume Bullets (When You Don't Work With Numbers)

Step 7: Finish with a strong conclusion

It’s tempting to treat the final lines of your cover letter as a throwaway: “I look forward to hearing from you.” But your closing paragraph is your last chance to emphasize your enthusiasm for the company or how you’d be a great fit for the position. You can also use the end of your letter to add important details—like, say, the fact that you’re willing to relocate for the job.

Try something like this:

“I believe my energy, desire to innovate, and experience as a sales leader will serve OrangePurple Co. very well. I would love to meet to discuss the value I could add as your next West Coast Sales Director. I appreciate your consideration and hope to meet with you soon.”

Then be sure to sign off professionally , with an appropriate closing and your first and last name. (Need help? Here are three cover letter closing lines that make hiring managers grimace, plus some better options .)

Step 8: Reread and revise

We shouldn’t have to tell you to run your cover letter through spell-check, but remember that having your computer scan for typos isn’t the same as editing . Set your letter aside for a day or even just a few hours, and then read through it again with fresh eyes—you’ll probably notice some changes you want to make.

You might even want to ask a friend or family member to give it a look. In addition to asking them if they spot any errors, you should ask them two questions:

• Does this sell me as the best person for the job?
• Does it get you excited?

If the answer to either is “no,” or even slight hesitation, go back for another pass.

Cover letter examples

Here are four example cover letters that follow the advice given above. Keep in mind that different situations may require adjustments in your approach. For instance, experienced job seekers can emphasize accomplishments from previous roles, while those with less experience might highlight volunteer work, personal projects, or skills gained through education.

Example #1: Cover letter for a job application

Alia Farhat San Francisco Bay Area [email protected] 444-000-1111

Hello Danny Tanaka,

If I’m being honest, I still haven’t fully gotten over the death of my first Tamagotchi pet when I was six years old. (His name was Tommy, and I’ve gotten far more creative since then, I promise.) When I was older, I discovered NeoPets and I was hooked for years—not just on the site, but on the community that surrounded it. So when I heard about FantasyPets last year, I immediately started following news about your development process, and that’s how I saw your post looking for a marketing strategist. Not only do I have eight years of experience in digital marketing, but as a lifelong gamer with a passion for pet-focused titles who’s spent years in online communities with like-minded people, I also know exactly what kind of messaging resonates with your target audience.

You’re looking for someone to help you craft a social media marketing campaign to go along with your game launch, and I’ve been a part of three launch-day marketing campaigns for mobile and web-based games. In my current role as social media manager at Phun Inc., I proposed a campaign across Twitter, Instagram, and TikTok based on competitor research and analysis of our social campaigns for similar games to go along with the launch of the mobile game FarmWorld. Using my strategy of featuring both kids and adults in ads, we ended up driving over one million impressions and 80k downloads in the first three months.

I’ve always believed that the best way to find the right messaging for a game is to understand the audience and immerse myself in it as much as possible. I spend some of my research time on gaming forums and watching Twitch streams and Let’s Plays to see what really matters to the audience and how they talk about it. Of course, I always back my strategies up with data—I’m even responsible for training new members of the marketing team at Phun Inc. in Google AdWords and data visualization.

I believe that my passion for games exactly like yours, my digital marketing and market research experience, and my flair for turning data into actionable insights will help put FantasyPets on the map. I see so much promise in this game, and as a future player, I want to see its user base grow as much as you do. I appreciate your consideration for the marketing strategist role and hope to speak with you soon.

Alia Farhat

Example #2: Cover letter for an internship

Mariah Johnson

New York, NY [email protected] 555-000-1234

Dear Hiring Manager,

I am excited to submit my application for the software development internship at Big Tech. As a student at New York University majoring in computer science with a keen interest in social studies, I believe I would be a good fit for the role. Big Tech's mission to promote equality and a more sustainable world is deeply inspiring, and I would be thrilled to contribute to this mission.

In a recent hackathon, I demonstrated my ability to lead a team in designing and developing an app that directs members of a small community to nearby electronics recycling centers. My team successfully developed a working prototype and presented it to a panel of industry experts who awarded us second place.

I’ve also been an active volunteer at my local library for over four years. During this time, I organized book donation drives, led book fairs, and conducted reading sessions with children. This experience strengthened my presentation and communication skills and confirmed my motivation stems from supporting a good cause. I would be more than happy to bring my passion and dedication to an organization whose mission resonates with me..

Through these experiences, along with my coursework in software engineering, I am confident I am able to navigate the challenges of the Big Tech internship program. I look forward to the opportunity to speak with you about my qualifications. Thank you for your consideration.

Example #3: Cover letter with no experience

Sarah Bergman

Philadelphia, PA [email protected] 1234-555-6789

Dear Chloe West,

I’m excited to apply for the entry-level copywriting position at Idea Agency. As a recent graduate from State University with a major in mass communications, I’m eager to delve deeper into copywriting for brands, marketing strategies, and their roles in the business world.

Over the past two years, I’ve completed courses in creative writing, copywriting, and essentials of digital marketing. I’ve also been actively involved in extracurricular activities, creating content and promoting student events across multiple online platforms. These experiences expanded my creativity, enhanced my teamwork skills, and strengthened my communication abilities.

As an admirer of your visionary marketing campaigns and Idea Agency’s commitment to sustainability, I’m enthusiastic about the prospect of joining your team. I'm confident that I can contribute to your future projects with inventive thinking and creative energy.

I welcome the opportunity to discuss my qualifications further. Thank you for considering my application.

Best regards,

Example #4: Career change cover letter

Leslie Smith

Chicago, IL [email protected] 111-222-3344

Dear Paul Jones,

Over the past year, I’ve volunteered to represent my company at a local fair and there I discovered how much fun working face to face with clients would be. Everytime I sold a product for The Solar Company, I often wished it was my full-time job. Now, I'm excited to submit my application for the sales coordinator position with Bloom Sales.

After completing a degree in business administration, I decided to put my outgoing personality and strong communication skills to work as a sales specialist at The Solar Company. I’ve sharpened my presentation and critical thinking skills in client meetings and sourced more than $20,000 in new partnerships. This experience has given me an invaluable foundation, and now I’m confident it's the time to move business administration to sales coordination.

I’m comfortable seeking out new business opportunities, making cold calls, and selling potential clients on the advantages of Bloom Sales products. I attend an average of 10 in-person meetings a week, and interacting with a lot of different personalities is what excites me the most. As a detail-oriented, tech-savvy professional, I have advanced knowledge of Excel and data analysis.

I would love to learn more about your sales strategy for the second semester and discuss how my experience in business administration and client-facing sales exposure would help Bloom Sales achieve its goals. Thank you for your consideration.

Extra cover letter examples

• Pain point cover letter example
• Recent graduate cover letter example
• Stay-at-home parent returning to work cover letter example
• Sales cover letter example
• Email marketing manager cover letter example
• No job description or position cover letter example (a.k.a., a letter of intent or interest)
• Buzzfeed-style cover letter example
• Creative cover letter example (from the point-of-view of a dog)

Bonus cover letter tips to give you an edge over the competition

As you write your cover letter, here are a few more tips to consider to help you stand out from the stack of applicants:

• Keep it short and sweet: There are always exceptions to the rule, but in general, for resumes and cover letters alike, don’t go over a page. (Check out these tips for cutting down your cover letter .)
• Never apologize for your missing experience: When you don’t meet all of the job requirements, it’s tempting to use lines like, “Despite my limited experience as a manager…” or “While I may not have direct experience in marketing…” But why apologize ? Instead of drawing attention to your weaknesses, emphasize the strengths and transferable skills you do have.
• Strike the right tone: You want to find a balance between being excessively formal in your writing—which can make you come off as stiff or insincere—and being too conversational. Let your personality shine through, for sure, but also keep in mind that a cover letter shouldn’t sound like a text to an old friend.
• Consider writing in the company’s “voice:” Cover letters are a great way to show that you understand the environment and culture of the company and industry. Spending some time reading over the company website or stalking their social media before you get started can be a great way to get in the right mindset—you’ll get a sense for the company’s tone, language, and culture, which are all things you’ll want to mirror—especially if writing skills are a core part of the job.
• Go easy on the enthusiasm: We can’t tell you how many cover letters we’ve seen from people who are “absolutely thrilled for the opportunity” or “very excitedly applying!” Yes, you want to show personality, creativity, and excitement. But downplay the adverbs a bit, and keep the level of enthusiasm for the opportunity genuine and believable.

The bottom line with cover letters is this: They matter, much more than the naysayers will have you believe. If you nail yours, you could easily go from the “maybe” pile straight to “Oh, hell yes.”

Cover letter FAQs (a.k.a., everything else you need to know about cover letters)

• Are cover letters still necessary?
• Do I have to write a cover letter if it’s optional?
• Can I skip the cover letter for a tech job?
• What does it mean to write a cover letter for a resume?
• How can I write a simple cover letter in 30 minutes?
• How can I show personality in my cover letter?
• What should I name my cover letter file?
• Is a letter of intent different from a cover letter?
• Is a letter of interest different from a cover letter?

Regina Borsellino , Jenny Foss , and Amanda Cardoso contributed writing, reporting, and/or advice to this article.

Resume Templates

Resume samples

Create and edit your resume online

Generate compelling resumes with our AI resume builder and secure employment quickly.

Write a cover letter

Cover Letter Examples

Cover Letter Samples

Create and edit your cover letter

Use our user-friendly tool to create the perfect cover letter.

Featured articles

• How to Write a Motivation Letter With Examples
• How to Write a Resume in 2024 That Gets Results
• Teamwork Skills on Your Resume: List and Examples
• What Are the Best Colors for Your Resume?

Latests articles

• Key Advice Before You Sign Your Next Work Contract in 2024
• Resume Review With AI: Boost Your Application with Ease
• Top AI Skills for a Resume: Benefits and How To Include Them
• Top 5 Tricks to Transform Your LinkedIn Profile With ChatGPT

Dive Into Expert Guides to Enhance your Resume

The Ultimate Cover Letter Writing Guide

The complete guide to writing an effective cover letter.

Any of these sound familiar? The simple answer is yes, having an effective cover letter is completely necessary and highly recommended and we’ll tell you  why you need a cover letter as well as a resume!

When you’re applying for a job, whether it be for an  entry-level  position after graduating or for a high-level executive vacancy with a  professional resume , a  cover letter is essential to make your application stand out .

Without this extra introductory letter, a resume alone could easily be discarded by a hiring manager. CareerBuilder  estimates you’re  10% more likely to miss out on an opening  if you don’t include a cover letter.

Writing a good cover letter  it’s not a skill many many people master, but that doesn’t mean it’s an impossible feat!

With our complete  cover letter guide , you’ll learn  how to write a cover letter  that will attract the hiring manager and convince them to read your winning resume.

What is a cover letter?

A cover letter is an extension to your job application.  It is not obligatory but including a well-written cover letter is  strongly advised by all human resource experts . By definition, a cover letter is an accompanying, explanatory letter.

All  jobseekers need a sales pitch  of sorts, they need to hook the reader and demonstrate to the hiring manager why they are the right person for the vacancy on offer. This style of  self-marketing for a job application  must come in the form of a  winning resume and cover letter combination  that complement one another.

A simple cover letter is an introduction to the candidate  behind the qualifications and experience. The aim is to show a prospective employer how you can take on the role and  what you can offer the company  in question.

Cover letters generally  follow a basic structure  and can be in either hard or digital format, that is to say, either printed and sent via regular mail or as a document scanned and attached to send digitally, or written directly in an  email cover letter .

Why include a cover letter on a job application?

If you want to stand any chance at all of  catching the eye of a potential employer , it is  imperative to include a cover letter  with your job application.

Simple – even if you  create an effective, outstanding resume , using all the right keywords and qualifications etc. it’s possible there are candidates more qualified than you or with more experience so it’s necessary to  add a cover letter to back up your resume  and allow the hiring manager to see more of your personal side that is relevant to the vacancy.

• The cover letter demonstrates your communication skills.
• The cover letter serves as an introduction to the resume.
• The cover letter can be used to emphasize certain skills, or mention skills that you couldn’t fit on the resume (it serves as an addendum).
• The cover letter is what you customize for each position, to show why you are the right person for “That” role, as opposed to the resume which stays pretty much the same for all applications.

A cover letter is the added value  that you need in a job application to ensure the call-back you’ve been waiting for.

To  create a unique, tailor-made job application , each candidate should use a cover letter to highlight their strengths and  elaborate on relevant achievements  that demonstrate their ability to take on the new responsibilities.

Is it practically always sensible and  appropriate to write a cover letter to accompany a resume for a job application  that should be customized for the role you’re applying to including any explanations of information that might be missing from the resume, such as employment gaps, traveling, periods of study etc.

The only time it is acceptable to not include a cover letter in your job application is if the job listing specifically requests that you do not.

Advantages of Writing a Cover Letter

A cover letter directly adds to the likelihood that you are called in for an interview and  gives you a better chance of being hired .

If you’re successful in  writing an effective cover letter , it will offer you the following advantages:

• Hiring managers will see your added effort
• Demonstrates you put in the time to learn about the company
• It will add a personal touch to your application
• It shows your enthusiasm for the opening
• Hiring managers will become acquainted with your best qualities

Knowing exactly what is in a cover letter will ensure that it gives you a  major advantage  over the other applicants.

What are the 3 Types of Cover Letters?

Adding a cover letter is almost always essential, but  choosing the appropriate letter  will also be key. Depending on the job post you are applying for, you will need to select the best type of letter to send along with your resume.

There are  3 types of cover letters  that you can send to a hiring manager. The 3 types are:

• Application cover letters
• Letters of Interest
• Email Cover letters

The letter you write is influenced by  whether you are going to apply for a job directly , citing a referral, or asking about vacancies that are not advertised.

Whatever the case may be, ensure that the cover letter is  specific to the job vacancy . It’s always important to avoid making a generic cover letter for every single job you apply for.

So, what are the 3 types of cover letters you should consider sending to a job recruiter?

Application Cover Letter

This is your  classic cover letter  that you send to a hiring manager when you spot a company advertising a job opening. When you want to directly apply for a position, it is mandatory to send this, unless you are specifically asked not to.

Using this letter, you can mention why you want to work for a specific company and why you are the perfect candidate for the position.

Letter of Interest

Say you notice a company that you would really like to work for. It fits your sector, and you know it offers great benefits and good pay. However, you  can’t find any openings  that match your skill set.

If that’s the case, you don’t need to sit around and wait for the company to have a job vacancy. You can take action with a letter of interest. This type of cover letter  states your interest in being employed  by a company that isn’t currently advertising any vacancies.

This type of letter goes by a couple of other names, such as:

• Letter of intent
• Statement of interest

Of course, since there is no vacancy there is no role you can specifically mention, which is the major difference between a letter of intent and a traditional cover letter. Your objective will be to  advertise yourself well enough  that an employer will just have to interview you.

Email Cover Letters

Over the years, the job application process has shifted to a nearly  100% online hiring process . Due to this, it may be necessary to send your cover letter  in an email  as part of your job application.

While applying, there may not be an option to upload your cover letter. Or maybe you would just like to send it in the  body of your email along with your resume . You can send it in one of two ways, in the body of your email or as an attachment (in PDF).

How to write a cover letter

A cover letter, although  short in length  generally, can take time to elaborate as it is important to get it right. Sometimes, due to the scarce space for writing, candidates find it difficult to know  what to include in a cover letter  and  what to leave out .

However, knowing  how to do a cover letter  can make all the difference to your job application and be the just the thing to capture the attention of a hiring manager.

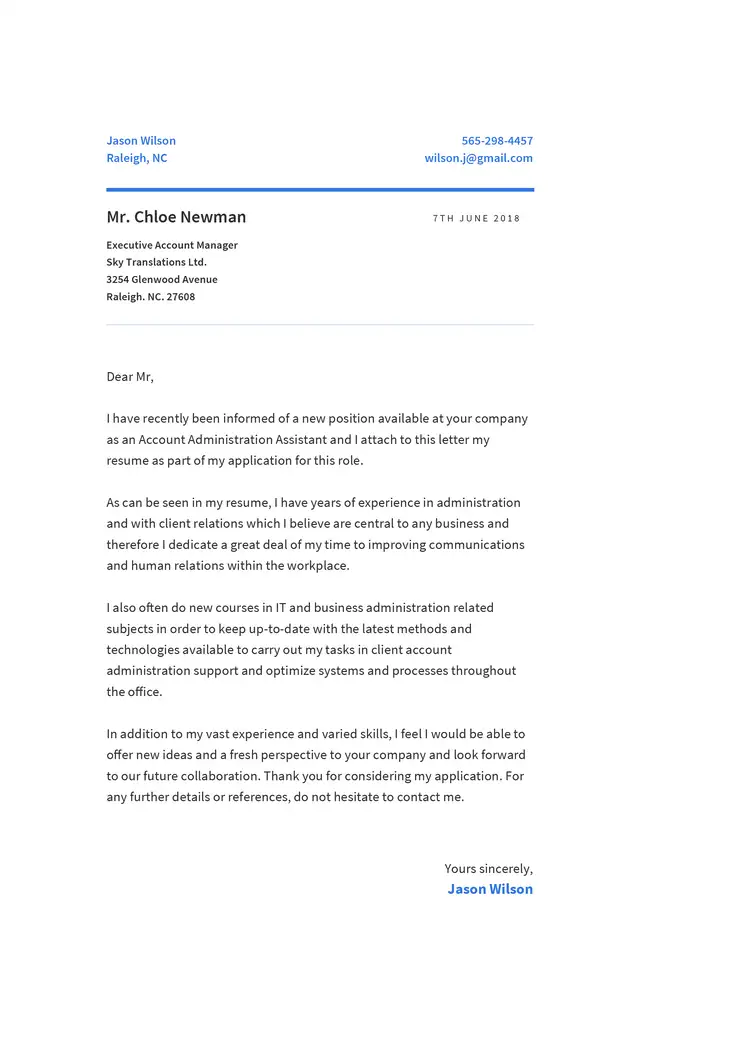
A  professional cover letter  should be well-formatted, following a structure with a header, an opening paragraph, a second main paragraph, a final closing paragraph and a closing with signature/electronic signature.

To  begin writing a cover letter for a job application , candidates should analyze their skills, qualifications, accomplishments and experience to  decide which are the most fundamental aspects to include  in their personalized cover letter.

Next, each jobseeker will have to  select the most job-relevant  of these elements to include by  comparing them with the required or desired qualifications and experience  in the job description.

Finally, the applicant should choose some  memorable examples which demonstrate evidence  of each element included in their cover letter, aiming to  tell a story  which shows their aptitude concerning each skill or qualification.

Jobseekers should also ensure to explore  how to make a cover letter  for their specific role or industry because, similarly to resumes, each cover letter should be  tailored for the vacancy  and company to which it will be sent.

It is vital for candidates to  consider several factors when it comes to writing their professional cover letter . A jobseeker must review their  resume work history section  as well as any skills and honors included to find the  most pertinent experiences  that can be explored further. Detailing examples of when a candidate demonstrated certain abilities or expertise is how a candidate can convince a hiring.

One way to create a winning cover letter is to use an  online cover letter creator  or take advantage of cover letter templates as a stepping stone as well as checking out cover letter examples that can serve as a great source of inspiration for you to make your own  unique cover letter .

Our  cover letter builder  forms part of our resume builder and allows jobseekers to create a more complete job application. Users can write their cover letter with pro tips and design help thanks to our pre-designed templates. Read our  cover letter writing guide  to get to grips with  cover letter writing techniques  and tips before using our online cover letter builder!

How to Structure a Cover Letter

The  structure and layout of a cover letter  is essential to make sure the letter displays each point that you wish to get across  clearly and concisely . This means it’s necessary, in general, to follow a commonly-accepted format for an effective cover letter.

Similarly to a  resume format , designing and  writing a cover letter has certain rules  which should be adhered to in order to convey the necessary information in a brief and to the point introductory letter.

Check out some of the  cover letter best practices  as advised by human resources experts below:

• It’s imperative to  begin a cover letter with a header , including the candidate’s name and contact information as well as the date. This  primary cover letter section  can also include the job title, website and other relevant personal information.

Following this, the  letter should include the details of the company  and person to whom you are writing, with the full name, job title or team, company name and address.

• The main body of a cover letter should be divided into  three sections : an introduction, a bullet list of accomplishments followed by a paragraph highlighting skills, and a closing paragraph inviting the hiring manager to contact you. By using bullet points when detailing your achievements and capabilities, you can make sure that recruiters will be able to quickly pick out key information. This is especially important as studies have found that recruiters spend very little time reading each individual application.
• Finally, the letter should be electronically or physically signed with your full name in a formal manner.

The universally-accepted  cover letter length  is no longer than one letter page, which in total has about  250-300 words  for the main body of text.

Don’t  repeat information  or be too detailed because hiring managers simply do not have the time to read it all and will simply skip to the next one.  Resumes that run over 600 words  get rejected 43% faster and cover letters can easily fall into this trap too.

Keep your cover letter short and sweet and to the point!

Get more  cover letter formatting advice  in our guide on  how to format a cover letter  with tips and information about all aspects of a good cover letter structure.

Cover letter advice

The  importance of including a cover letter  with your job application is often overlooked by jobseekers of all categories, however this can seriously reduce your possibilities of getting an interview with a prospective employer.

Therefore you need not ask yourself  when to write a cover letter  because the answer is just that simple – it is  always appropriate to include a cover letter in your job application , unless the listing explicitly requests that you do not.

Check out the following  expert cover letter tips  to create a winning cover letter that will convince the hiring manager to give you a call:

• We may be quite repetitive with this one but the sheer quantity of resumes and cover letters that are disregarded simply for forgetting this  vital and basic rule  is incredible:  USE A PROFESSIONAL EMAIL ADDRESS  for your contact details and that does not include your current work email but a personal, suitable email address.
• It is essential to remember to  maintain your focus on the needs of the company  you’re applying to and the requirements and desired abilities of the ideal candidate for the role.  Do not focus on how you can benefit  by becoming a member of their team, but on how the team can make the most of your experience and knowledge.
• Remember to  highlight your transferable skills , especially in cases where you may not meet all the required qualities in the job description such as in student resumes and cover letters.
• Each  cover letter for a job application, cover letters for internships , for further study or even volunteer experience should be  tailored to their specific organization  and position with the pertinent keywords.
• Use specific examples to demonstrate the candidate’s individual capacity to take on the role and  tell a story with your cover letter  to convey more of your personality and passion towards the sector or profession.
• Towards the  end of a cover letter , each candidate should write a convincing finish to entice the hiring manager and in sales terminology “ seal the deal ”.
• Finally when you have completed your polished cover letter, potentially  one of the most important steps  in the process is to  PROOFREAD . Candidates should request that a friend, mentor, teacher or peer takes a look at their cover letter for not only  grammatical and spelling errors  but also any  unwanted repetition or unrelated information .

Some jobseekers doubt  whether a cover letter is necessary or not , but as most human resource professionals agree without a well-written cover letter, candidates lose the  possibility to demonstrate different aspects of their profile  from those included in their resumes which could easily be the deciding factor in your application!

An easy and fast way to write an effective cover letter for a job application is to employ an  online cover letter creator  that will offer advice on  how to complete a cover letter with examples  and HR-approved templates.

Cover Letter FAQs

What do employers look for in a cover letter, can a cover letter be two pages, what is the difference between a cover letter and a resume, should you put a photo on a cover letter.

Trouble getting your Cover Letter started?

Beat the blank page with expert help.

How it works

Transform your enterprise with the scalable mindsets, skills, & behavior change that drive performance.

Explore how BetterUp connects to your core business systems.

We pair AI with the latest in human-centered coaching to drive powerful, lasting learning and behavior change.

Build leaders that accelerate team performance and engagement.

Unlock performance potential at scale with AI-powered curated growth journeys.

Build resilience, well-being and agility to drive performance across your entire enterprise.

Transform your business, starting with your sales leaders.

Unlock business impact from the top with executive coaching.

Foster a culture of inclusion and belonging.

Accelerate the performance and potential of your agencies and employees.

See how innovative organizations use BetterUp to build a thriving workforce.

Discover how BetterUp measurably impacts key business outcomes for organizations like yours.

A demo is the first step to transforming your business. Meet with us to develop a plan for attaining your goals.

• What is coaching?

Learn how 1:1 coaching works, who its for, and if it's right for you.

Accelerate your personal and professional growth with the expert guidance of a BetterUp Coach.

Types of Coaching

Navigate career transitions, accelerate your professional growth, and achieve your career goals with expert coaching.

Enhance your communication skills for better personal and professional relationships, with tailored coaching that focuses on your needs.

Find balance, resilience, and well-being in all areas of your life with holistic coaching designed to empower you.

Discover your perfect match : Take our 5-minute assessment and let us pair you with one of our top Coaches tailored just for you.

Research, expert insights, and resources to develop courageous leaders within your organization.

Best practices, research, and tools to fuel individual and business growth.

View on-demand BetterUp events and learn about upcoming live discussions.

The latest insights and ideas for building a high-performing workplace.

• BetterUp Briefing

The online magazine that helps you understand tomorrow's workforce trends, today.

Innovative research featured in peer-reviewed journals, press, and more.

Founded in 2022 to deepen the understanding of the intersection of well-being, purpose, and performance

We're on a mission to help everyone live with clarity, purpose, and passion.

Join us and create impactful change.

Read the buzz about BetterUp.

Meet the leadership that's passionate about empowering your workforce.

For Business

For Individuals

How to write a great cover letter in 2024: tips and structure

A cover letter is a personalized letter that introduces you to a potential employer, highlights your qualifications, and explains why you're a strong fit for a specific job.

Hate or love them, these brief documents allow job seekers to make an impression and stand out from the pile of other applications. Penning a thoughtful cover letter shows the hiring team you care about earning the position.

Here’s everything you need to know about how to write a cover letter — and a great one, at that.

What is a cover letter and why does it matter?

A professional cover letter is a one-page document you submit alongside your CV or resume as part of a job application. Typically, they’re about half a page or around 150–300 words.

An effective cover letter doesn’t just rehash your CV; it’s your chance to highlight your proudest moments, explain why you want the job, and state plainly what you bring to the table.

Show the reviewer you’re likable, talented, and will add to the company’s culture . You can refer to previous jobs and other information from your CV, but only if it helps tell a story about you and your career choices .

What 3 things should you include in a cover letter?

A well-crafted cover letter can help you stand out to potential employers. To make your cover letter shine, here are three key elements to include:

1. Personalization

Address the hiring manager or recruiter by name whenever possible. If the job posting doesn't include a name, research to find out who will be reviewing applications. Personalizing your cover letter shows that you've taken the time to tailor your application to the specific company and role.

2. Highlight relevant achievements and skills

Emphasize your most relevant skills , experiences, and accomplishments that directly relate to the job you're applying for. Provide specific examples of how your skills have benefited previous employers and how they can contribute to the prospective employer's success. Use quantifiable achievements , such as improved efficiency, cost savings, or project success, to demonstrate your impact.

3. Show enthusiasm and fit

Express your enthusiasm for the company and the position you're applying for. Explain why you are interested in this role and believe you are a good fit for the organization. Mention how your values, goals, and skills align with the company's mission and culture. Demonstrating that you've done your research can make a significant impression.

What do hiring managers look for in a cover letter?

Employers look for several key elements in a cover letter. These include:

Employers want to see that your cover letter is specifically tailored to the position you are applying for. It should demonstrate how your skills, experiences, and qualifications align with the job requirements.

Clear and concise writing

A well-written cover letter is concise, easy to read, and error-free. Employers appreciate clear and effective communication skills , so make sure your cover letter showcases your ability to express yourself effectively.

Demonstrated knowledge of the company

Employers want to see that you are genuinely interested in their organization. Mention specific details about the company, such as recent achievements or projects, to show that you are enthusiastic about joining their team.

Achievements and accomplishments

Highlight your relevant achievements and accomplishments that demonstrate your qualifications for the position. Use specific examples to showcase your skills and show how they can benefit the employer.

Enthusiasm and motivation

Employers want to hire candidates who are excited about the opportunity and motivated to contribute to the company's success. Express your enthusiasm and passion for the role and explain why you are interested in working for the company.

Professionalism

A cover letter should be professional in tone and presentation. Use formal language, address the hiring manager appropriately, and follow standard business letter formatting.

How do you structure a cover letter?

A well-structured cover letter follows a specific format that makes it easy for the reader to understand your qualifications and enthusiasm for the position. Here's a typical structure for a cover letter:

Contact information

Include your name, address, phone number, and email address at the top of the letter. Place your contact information at the beginning so that it's easy for the employer to reach you.

Employer's contact information

Opening paragraph, middle paragraph(s), closing paragraph, complimentary close, additional contact information.

Repeat your contact information (name, phone number, and email) at the end of the letter, just in case the employer needs it for quick reference.

Remember to keep your cover letter concise and focused. It should typically be no more than one page in length. Proofread your letter carefully to ensure it is free from spelling and grammatical errors. Tailor each cover letter to the specific job application to make it as relevant and impactful as possible.

How to write a good cover letter (with examples)

The best letters are unique, tailored to the job description, and written in your voice — but that doesn’t mean you can’t use a job cover letter template.

Great cover letters contain the same basic elements and flow a certain way. Take a look at this cover letter structure for ref erence while you construct your own.

1. Add a header and contact information

While reading your cover letter, the recruiter shouldn’t have to look far to find who wrote it. Your document should include a basic heading with the following information:

• Pronouns (optional)
• Location (optional)
• Email address
• Phone number (optional)
• Relevant links, such as your LinkedIn profile , portfolio, or personal website (optional)

You can pull this information directly from your CV. Put it together, and it will look something like this:

Christopher Pike

San Francisco, California

[email protected]

Alternatively, if the posting asks you to submit your cover letter in the body of an email, you can include this information in your signature. For example:

Warm regards,

Catherine Janeway

Bloomington, Indiana

[email protected]

(555) 999 - 2222

2. Include a personal greeting

Always begin your cover letter by addressing the hiring manager — preferably by name. You can use the person’s first and last name. Make sure to include a relevant title, like Dr., Mr., or Ms. For example, “Dear Mr. John Doe.”

Avoid generic openings like “To whom it may concern,” “Dear sir or madam,” or “Dear hiring manager.” These introductions sound impersonal — like you’re copy-pasting cover letters — and can work against you in the hiring process.

Be careful, though. When using someone’s name, you don’t want to use the wrong title or accidentally misgender someone. If in doubt, using only their name is enough. You could also opt for a gender-neutral title, like Mx.

Make sure you’re addressing the right person in your letter — ideally, the person who’s making the final hiring decision. This isn’t always specified in the job posting, so you may have to do some research to learn the name of the hiring manager.

3. Draw them in with an opening story

The opening paragraph of your cover letter should hook the reader. You want it to be memorable, conversational, and extremely relevant to the job you’re pursuing. 

There’s no need for a personal introduction — you’ve already included your name in the heading. But you should make reference to the job you’re applying for. A simple “Thank you for considering my application for the role of [job title] at [company],” will suffice.

Then you can get into the “Why” of your job application. Drive home what makes this specific job and this company so appealing to you. Perhaps you’re a fan of their products, you’re passionate about their mission, or you love their brand voice. Whatever the case, this section is where you share your enthusiasm for the role.

Here’s an example opening paragraph. In this scenario, you’re applying for a digital marketing role at a bicycle company:

“Dear Mr. John Doe,

Thank you for considering my application for the role of Marketing Coordinator at Bits n’ Bikes.

My parents bought my first bike at one of your stores. I’ll never forget the freedom I felt when I learned to ride it. My father removed my training wheels, and my mom sent me barrelling down the street. You provide joy to families across the country — and I want to be part of that.”

4. Emphasize why you’re best for the job

Your next paragraphs should be focused on the role you’re applying to. Highlight your skill set and why you’re a good fit for the needs and expectations associated with the position. Hiring managers want to know what you’ll bring to the job, not just any role.

Start by studying the job description for hints. What problem are they trying to solve with this hire? What skills and qualifications do they mention first or more than once? These are indicators of what’s important to the hiring manager.

Search for details that match your experience and interests. For example, if you’re excited about a fast-paced job in public relations, you might look for these elements in a posting:

• They want someone who can write social media posts and blog content on tight deadlines
• They value collaboration and input from every team member
• They need a planner who can come up with strong PR strategies

Highlight how you fulfill these requirements:

“I’ve always been a strong writer. From blog posts to social media, my content pulls in readers and drives traffic to product pages. For example, when I worked at Bits n’ Bikes, I developed a strategic blog series about bike maintenance that increased our sales of spare parts and tools by 50% — we could see it in our web metrics.

Thanks to the input of all of our team members, including our bike mechanics, my content delivered results.”

5. End with a strong closing paragraph and sign off gracefully

Your closing paragraph is your final chance to hammer home your enthusiasm about the role and your unique ability to fill it. Reiterate the main points you explained in the body paragraphs and remind the reader of what you bring to the table.

You can also use the end of your letter to relay other important details, like whether you’re willing to relocate for the job.

When choosing a sign-off, opt for a phrase that sounds professional and genuine. Reliable options include “Sincerely” and “Kind regards.”

Here’s a strong closing statement for you to consider:

“I believe my enthusiasm, skills, and work experience as a PR professional will serve Bits n’ Bikes very well. I would love to meet to further discuss my value-add as your next Director of Public Relations. Thank you for your consideration. I hope we speak soon.

Tips to write a great cover letter that compliments your resume

When writing your own letter, try not to copy the example excerpts word-for-word. Instead, use this cover letter structure as a baseline to organize your ideas. Then, as you’re writing, use these extra cover letter tips to add your personal touch:

• Keep your cover letter different from your resume : Your cover letter should not duplicate the information on your resume. Instead, it should provide context and explanations for key points in your resume, emphasizing how your qualifications match the specific job you're applying for.
• Customize your cover letter . Tailor your cover letter for each job application. Address the specific needs of the company and the job posting, demonstrating that you've done your homework and understand their requirements.
• Show enthusiasm and fit . Express your enthusiasm for the company and position in the cover letter. Explain why you are interested in working for this company and how your values, goals, and skills align with their mission and culture.
• Use keywords . Incorporate keywords from the job description and industry terms in your cover letter. This can help your application pass through applicant tracking systems (ATS) and demonstrate that you're well-versed in the field.
• Keep it concise . Your cover letter should be succinct and to the point, typically no more than one page. Focus on the most compelling qualifications and experiences that directly support your application.
• Be professional . Maintain a professional tone and structure in your cover letter. Proofread it carefully to ensure there are no errors.
• Address any gaps or concerns . If there are gaps or concerns in your resume, such as employment gaps or a change in career direction, briefly address them in your cover letter. Explain any relevant circumstances and how they have shaped your qualifications and determination.
• Provide a call to action . Conclude your cover letter with a call to action, inviting the employer to contact you for further discussion. Mention that you've attached your resume for their reference.
• Follow the correct format . Use a standard cover letter format like the one above, including your contact information, a formal salutation, introductory and closing paragraphs, and your signature. Ensure that it complements your resume without redundancy.
• Pick the right voice and tone . Try to write like yourself, but adapt to the tone and voice of the company. Look at the job listing, company website, and social media posts. Do they sound fun and quirky, stoic and professional, or somewhere in-between? This guides your writing style.
• Tell your story . You’re an individual with unique expertise, motivators, and years of experience. Tie the pieces together with a great story. Introduce how you arrived at this point in your career, where you hope to go , and how this prospective company fits in your journey. You can also explain any career changes in your resume.
• Show, don’t tell . Anyone can say they’re a problem solver. Why should a recruiter take their word for it if they don’t back it up with examples? Instead of naming your skills, show them in action. Describe situations where you rose to the task, and quantify your success when you can.
• Be honest . Avoid highlighting skills you don’t have. This will backfire if they ask you about them in an interview. Instead, shift focus to the ways in which you stand out.
• Avoid clichés and bullet points . These are signs of lazy writing. Do your best to be original from the first paragraph to the final one. This highlights your individuality and demonstrates the care you put into the letter.
• Proofread . Always spellcheck your cover letter. Look for typos, grammatical errors, and proper flow. We suggest reading it out loud. If it sounds natural rolling off the tongue, it will read naturally as well.

Common cover letter writing FAQs

How long should a cover letter be.

A cover letter should generally be concise and to the point. It is recommended to keep it to one page or less, focusing on the most relevant information that highlights your qualifications and fits the job requirements.

Should I include personal information in a cover letter?

While it's important to introduce yourself and provide your contact information, avoid including personal details such as your age, marital status, or unrelated hobbies. Instead, focus on presenting your professional qualifications and aligning them with the job requirements.

Can I use the same cover letter for multiple job applications?

While it may be tempting to reuse a cover letter, it is best to tailor each cover letter to the specific job you are applying for. This allows you to highlight why you are a good fit for that particular role and show genuine interest in the company.

Do I need to address my cover letter to a specific person?

Whenever possible, it is advisable to address your cover letter to a specific person, such as the hiring manager or recruiter. If the job posting does not provide this information, try to research and find the appropriate contact. If all else fails, you can use a generic salutation such as "Dear Hiring Manager."

Should I include references in my cover letter?

It is generally not necessary to include references in your cover letter. Save this information for when the employer explicitly requests it. Instead, focus on showcasing your qualifications and achievements that make you a strong candidate for the position.

It’s time to start writing your stand-out cover letter

The hardest part of writing is getting started. 

Hopefully, our tips gave you some jumping-off points and confidence . But if you’re really stuck, looking at cover letter examples and resume templates will help you decide where to get started. 

There are numerous sample cover letters available online. Just remember that you’re a unique, well-rounded person, and your cover letter should reflect that. Using our structure, you can tell your story while highlighting your passion for the role. 

Doing your research, including strong examples of your skills, and being courteous is how to write a strong cover letter. Take a breath , flex your fingers, and get typing. Before you know it, your job search will lead to a job interview.

If you want more personalized guidance, a specialized career coach can help review, edit, and guide you through creating a great cover letter that sticks.

Ace your job search

Explore effective job search techniques, interview strategies, and ways to overcome job-related challenges. Our coaches specialize in helping you land your dream job.

Elizabeth Perry, ACC

Elizabeth Perry is a Coach Community Manager at BetterUp. She uses strategic engagement strategies to cultivate a learning community across a global network of Coaches through in-person and virtual experiences, technology-enabled platforms, and strategic coaching industry partnerships. With over 3 years of coaching experience and a certification in transformative leadership and life coaching from Sofia University, Elizabeth leverages transpersonal psychology expertise to help coaches and clients gain awareness of their behavioral and thought patterns, discover their purpose and passions, and elevate their potential. She is a lifelong student of psychology, personal growth, and human potential as well as an ICF-certified ACC transpersonal life and leadership Coach.

3 cover letter examples to help you catch a hiring manager’s attention

Chatgpt cover letters: how to use this tool the right way, how to write an impactful cover letter for a career change, write thank you letters after interviews to stand out as job applicant, send a thank you email after an internship to boost your career, character references: 4 tips for a successful recommendation letter, use professional reference templates to make hiring smoother, tips and tricks for writing a letter of interest (with examples), what is a letter of intent examples on how to write one, how to ask for a letter of recommendation (with examples), how to write a resume summary that works + examples, how to quit a part-time job: 5 tips to leave on good terms, how to write a follow-up email 2 weeks after an interview, how to create a resume with chatgpt, how and when to write a functional resume (with examples), cv versus resume demystify the differences once and for all, how to cancel an interview but keep your job outlook bright, what are professional references and how to ask for one (examples), stay connected with betterup, get our newsletter, event invites, plus product insights and research..

3100 E 5th Street, Suite 350 Austin, TX 78702

• Platform Overview
• Integrations
• Powered by AI
• BetterUp Lead™
• BetterUp Manage™
• BetterUp Care®
• Sales Performance
• Diversity & Inclusion
• Case Studies
• Why BetterUp?
• About Coaching
• Find your Coach
• Career Coaching
• Communication Coaching
• Life Coaching
• News and Press
• Leadership Team
• Become a BetterUp Coach
• BetterUp Labs
• Center for Purpose & Performance
• Leadership Training
• Business Coaching
• Contact Support
• Contact Sales
• Privacy Policy
• Acceptable Use Policy
• Trust & Security
• Cookie Preferences

18 Free Cover Letter Templates That Will Actually Get You Interviews

Simple Cover Letter

Creative Cover Letter

Professional Cover Letter

Jobscan’s cover letter templates are clean and professional . We intentionally avoided using flashy colors and design elements when creating them. Why?

Because most companies nowadays use applicant tracking systems (ATS) to screen resumes and cover letters. These systems can struggle to read and interpret visually complex documents.

This means your beautifully designed, eye-catching cover letter might remain stuck in an ATS database, never to be seen by an actual human being.

By using one of our simple, easy-to-read templates, you’ll significantly improve the chances that your cover letter will successfully pass through an ATS and into the hands of a hiring manager.

It’s super easy to get started too! Simply click the download button to get your hands on a Word document that you can customize to fit your unique situation.

When you’re done writing your cover letter, run it through Jobscan’s ATS-friendly cover letter checker to get personalized feedback on how to improve your letter and make it even more compelling to employers.

Basic Cover Letter

Formal Cover Letter

Career Change Cover Letter

Operations Manager Cover Letter

Pharmacy Technician Cover Letter

Project Management Cover Letter

Prospecting Cover Letter

Engineer Cover Letter

Supervisor Cover Letter

Human Resources Cover Letter

Intern Cover Letter

Marketing Cover Letter

Networking Cover Letter

Communications Cover Letter

Changing Careers Cover Letter

What is a cover letter?

It’s a letter of introduction that you send along with your resume when you apply for a job.

The key thing to remember about your cover letter is that it shouldn’t simply regurgitate your resume. Instead, it should support it.

Your cover letter can do this by:

• Explaining why you’re excited about the job opportunity.
• Showing how your skills and experience match the job requirements.
• Addressing any gaps in your work history.
• Showing off your personality (but not too much!).

By highlighting your strengths and showing your passion for the role and the company, your cover letter can make a strong case for why you deserve an interview.

NOTE : Get inspired by our expertly crafted cover letter examples and learn what makes each one shine. Our examples cover a wide range of jobs, industries, and situations, providing the guidance you need to create a winning cover letter.

Are cover letters necessary in 2023?

While some companies may not require one, a cover letter can still set you apart from other applicants and increase your chances of landing an interview.

In one survey , 83 percent of hiring managers said cover letters played an important role in their hiring decision.

In fact, most of the respondents in that survey claimed that a great cover letter might get you an interview even if your resume isn’t strong enough.

So don’t skip the cover letter ! When done correctly, it can be a powerful tool in your job search toolkit.

Why should you use a cover letter template?

Here are the 5 main reasons why you should use a cover letter template .

• It saves you time by creating personalized letters quickly and easily.
• It provides a framework or structure for your cover letter.
• It ensures that all the necessary information is included.
• It makes it easy to customize your cover letters for multiple applications.
• It helps you create a professional and polished cover letter without starting from scratch.

A template helps you streamline the cover letter writing process. This means you can devote more time and energy to other important aspects of your job search, such as networking and researching potential employers.

Generate a personalized cover letter in as little as 5 seconds

Our AI-powered cover letter generator uses GPT-4 technology to create a personalized and ATS-friendly cover letter in one click.

What should you include in your cover letter?

Every cover letter format should include the following information:

Contact information : Your name, address, phone number, and email address should be at the top of the letter.

Greetings : Address the letter to the hiring manager or the person who will be reviewing your application.

Opening paragraph : State the position you’re applying for and explain how you found out about the job. You can also briefly mention why you’re interested in the position and the company.

Body paragraphs : Use one or two paragraphs to highlight your relevant skills, experience, and qualifications that match the job requirements. Provide specific examples of your accomplishments and how they show off your abilities.

Closing paragraph : Repeat your interest in the position and thank the hiring manager for considering your application. You can also include a sentence or two about why you believe you’d be a good fit for the company culture.

Closing : Conclude your cover letter with a professional sign-off, such as “Best regards,” or “Sincerely”.

Do you need a unique cover letter for every job?

Absolutely! Do NOT use the exact same cover letter and simply change the name of the company and the position.

Instead, tailor each cover letter to the position you’re applying for.

You can do this by highlighting how your skills and experience match the specific requirements and responsibilities of the position.

It’s crucial to include the keywords that are in the job posting.

Why? Because your application will most likely go straight into an ATS database. Hiring managers search through this database for suitable job candidates by typing keywords into the search bar.

If your cover letter includes these keywords , it will be seen by the hiring manager. If it doesn’t include these keywords, your cover letter will remain in the database.

Not sure if your cover letter is ATS-friendly? Try running it through Jobscan’s cover letter checker .

This easy-to-use tool analyzes your cover letter and compares it to the job listing. It then identifies the key skills and qualifications that you should focus on in your letter.

How to write a cover letter if you have no work experience

If you don’t have much work experience, writing a strong cover letter can be challenging. But you can still do it!

Here are some tips to help you out:

Hook the reader right away . Introduce yourself and explain why you are interested in the position. If possible, mention a specific aspect of the company or role that especially appeals to you.

Highlight your relevant skills and experience . Focus on the skills you’ve gained through school projects, internships, volunteer work, or extracurricular activities. Be sure to provide specific examples .

Showcase your enthusiasm and willingness to learn . Employers look for candidates who are eager to learn and grow. Use your cover letter to convey your enthusiasm for the role and your willingness to take on new challenges.

Close with a strong call to action . End your cover letter by requesting an interview or expressing your interest in discussing the position further.

Proofread your cover letter carefully and customize it for each position you apply for.

Cover letter do’s and don’ts

• Use a generic greeting, such as “ To Whom It May Concern .”
• Use a one-size-fits-all cover letter for all your job applications.
• Simply repeat your resume in your cover letter.
• Use overly casual or informal language.
• Write a long and rambling cover letter.
• Use jargon or technical terms that the hiring manager may not understand.
• Include irrelevant information or details.
• Send a cover letter with spelling or grammatical errors.
• Address the letter to a specific person or hiring manager, if possible.
• Include your contact information at the top of the document.
• Tailor your letter to the company and position you’re applying for.
• Use keywords from the job description.
• Highlight your relevant skills and experiences.
• Use specific, measurable results to demonstrate your abilities.
• Try to inject some of your personality into the cover letter.
• Proofread your letter carefully for errors.
• Run your cover letter through Jobscan’s cover letter checker .

Q: How long should a cover letter be?

Most cover letters are too long. The ideal length is around 250-400 words. Hiring managers probably won’t read anything longer.

Q: Should I use a PDF or a Word cover letter template?

Either one should be fine. Some older ATS might not accept PDFs, but this is rare these days. Always check the job listing. If it says to submit a Word resume, then do that. Otherwise, a PDF resume works just as well.

Q: Can I email my cover letter instead of sending a cover letter?

Yes, you can email your cover letter instead of sending a physical copy through the mail. In fact, many employers now prefer to receive cover letters and resumes via email or through an online application system.

Explore more cover letter resources

Cover Letter Formats

Cover Letter Tips

Cover Letter Examples

Cover Letter Writing Guide

Cover Letter Templates

/ any level of experience

Choose a Matching Cover Letter Template

Looking to create a cover letter that will help you stand out from the crowd? Try one of our 16 professional cover letter templates, each created to match our resume and CV templates. Pick a cover letter template that suits your needs and impress the hiring manager with a flawless job application!

Skill-Based

Traditional

Professional

Learn More About Cover Letters

How to Write a Cover Letter in 2024 + Examples

Cover Letter Format (w/ Examples & Free Templates)

60+ Cover Letter Examples in 2024 [For All Professions]

Free Cover Letter Sample to Copy and Use

Subject Line: Cover Letter for [Position], [Candidate Name]

[Company Address]

[Company City, State]

[Hiring Manager Email]

Introduction:

Introduce yourself, give a brief professional summary, and optionally, a top achievement. E.g. “My name is [Name] and I’m a [Role] with over X years of experience in [Activity]. Over the past years, I’ve helped X companies achieve [Goals]”

Express your interest in joining their firm. E.g. “I’m looking to join [Company] as [Role] and I’m very excited to help you with [Activity]”

Optionally, if you were referred or you just know someone at the firm, you can mention this here. E.g. “I learned about [Company] from a friend that’s currently working there as [Role], [Friend’s name]. I really like everything I’ve heard about the company and I think I would make a good fit.”

This is where you talk about your work experience and achievements at length. Mention how you excelled at your previous roles, what your most important responsibilities were, and so on.

Look at this as an opportunity to expand on whatever you wrote in your resume, and give the reader a better picture of what kind of tasks you worked on, what you accomplished, and so on. E.g “At my previous jobs as [Role], my duties were [Major 3 duties], and I specifically excelled at [Top accomplishment]. This accomplishment helped the company [Results driven].”

Want to really impress the hiring manager? You can mention what you know about the company and its culture here. E.g. “I’ve read a lot about [Company] and I really think I’d enjoy your democratic leadership style.”

Optionally, you can include a bulleted list of your top 3 accomplishments. For example:

[Example Box]

Some of my top achievements in recent years include:

Launching a successful online ads marketing campaign, driving 100+ leads within 2 months.

Overhauled a client’s advertising account, improving conversion rates and driving 15% higher revenue.

Improved the agency’s framework for ad account audits and created new standard operating procedures.

Conclusion & Call to Action:

Re-affirm your desire to join the company, as well as how you can contribute. E.g. “I’d love to become a part of [Company] as a [Role]. I believe that my skills in [Field] can help the company with [Goals].”

Thank the hiring manager for reading the cover letter and then wrap it all up with a call to action. E.g. “Thank you for considering my application. I look forward to hearing back from you and learning more about the position. Sincerely, [Name].”

Match Your Resume & Cover Letter

Want your application to stand out?

Match your cover letter with your resume & catch the recruiter’s attention!

Why Novorésumé?

Matching Cover Letters

To keep your job application consistent and professional, our Cover Letter templates perfectly match the resume templates.

Creative & Standard Templates

Whether you apply for a conservative industry like banking or a hype start-up, you can tailor our cover letter templates to fit your exact needs.

Expert Reviews

Oana Vintila

Career Counselor

Cover Letters are usually synonymous with formal and bland rambling that you write down hoping for an invite to a job interview. I just love it how Novorésumé has enhanced that and is offering you a tool to build proper arguments and structured discourse about who YOU ARE and what YOU CAN DO.

A real confidence booster, I tell you, seeing your motivation eloquently written!

Gabriela Tardea

Career Strategist, Coach & Trainer

The best thing about this platform when creating a Cover Letter as an addition to your resume is that the documents will match each other's design and font, creating eye-catching documents that recruiters/hiring managers will love.

You will be initially judged based on your papers, so why not make a first great impression?

Cover Letters Resources

What is a cover letter.

A cover letter is a one-page document that you submit alongside your resume or CV for your job application.

The main purpose of your cover letter is to:

Show your motivation for working at the company

Bring special attention to the most important parts of your work history

Explain how your work experience fits whatever the company is looking for

What your cover letter is NOT about , is rehashing whatever you already mentioned in your resume. Sure, you should mention the most important bits, but it should NOT be a literal copy-paste.

Keep in mind that recruiters will usually read your cover letter after scanning your resume and deciding if you’re qualified for the position.

Our cover letter templates match both our resume templates and our CV templates ! Make sure to check them out, too.

Why Use a Cover Letter Template?

A cover letter can complement your resume and increase your chances of getting hired.

But that's only if it's done right.

If your cover letter isn't the right length, is structured the wrong way, or doesn't match the style of your resume, it might do the opposite and hurt your application.

By using a cover letter template, you get a pre-formatted, professional, and recruiter-friendly document that’s ready to go. All YOU have to do is fill in the contents, and you’re all set.

What to Include in Your Cover Letter?

Every good cover letter has the following sections:

Header . Start your cover letter by writing down your own contact information, as well as the recruiter’s (recruiter name, company name, company address, etc…).

Greeting . Preferably, you want to address the recruiter by their last name (e.g. Dear Mr. Brown) or their full name, in case you’re not sure what their pronouns are (e.g. Dear Alex Brown). formal greeting for the recruiter.

Opening paragraph . This is the introduction to your resume. Here, you summarize your background info (“a financial analyst with X+ years of experience”), state your intent (“looking for X position at Company Y”), and summarize your top achievements to get the recruiter hooked.

Second paragraph . In the second paragraph, you explain how you’re qualified for the position by mentioning your skills, awards, certifications, etc., and why the recruiter should pick YOU.

Third paragraph . You talk about why you’re a good match for the company. Do you share common values? Is the company working on projects you’re interested in? Has this position always been your dream role?

Formal closing . Finally, you end the cover letter with a quick summary and a call to action (“I’m super excited to work with Company X. Looking forward to hearing from you!”).

How to Write a Great Cover Letter?

There’s a lot that goes into writing a great cover letter. If you want to get the full picture, you can check out our guide on how to write a cover letter .

For a quick summary, though, here are our top 4 cover letter tips :

Avoid Fluff . You want to be as specific as possible with your cover letter. Avoid vague statements like “I’m a good fit for the company because I’m a good critical thinker!”

Do Your Research. Most companies don’t like people who “spray and pray” - applying for dozens of jobs without giving them much thought. What they ARE looking for is someone who’s passionate about their field, the position, and even the company. So, research the companies you apply for as much as you can and show off your knowledge in your cover letter.

Don’t Use a One-Fits-All Cover Letter . As much as you can, try to tailor your cover letter to the job you’re applying for. Even if it’s something small, like addressing the hiring manager by their last name instead of “Dear Sir/Madam,” or mentioning something specific about the role or the company that you’re passionate about, it can help you prove that you’re not using the same generic cover letter to apply to dozens of jobs.

Back-Up Your Achievements with Data . When possible, back up your experience with data. Instead of saying, “I improved company revenue”, say “I managed to hit and exceed sales KPIs for 5 months in a row.”

How Long Should a Cover Letter Be?

Most recruiters agree that a cover letter should be brief and concise .

Optimally, that’s about half a page to one full page, and between 250 to 400 words long.

How Can I Write a Student Cover Letter?

You should write a student cover letter pretty much the same way you’d write a regular cover letter, with one key difference.

To make up for your lack of work experience, you should talk about the following:

Why do you want to work for the company and the position you’re applying for.

How your educational background has prepared you for the job.

How your skill set can help you stand out and excel at the job.

You also want to mention anything else that’s relevant to the job and that can prove your abilities, such as any internships, awards, honors, and the like.

In case you’re writing a cover letter for an internship , make sure to check out our guide.

How Can I Write a Cover Letter With No Experience?

If you’re an entry-level candidate, writing a cover letter might seem super scary. If you don’t have any work experience and professional accomplishments, what are you supposed to talk about in your cover letter?

Here’s some good news—you can focus on these topics instead:

Education highlights

Relevant skills

Independent projects

Volunteering experience

Extracurricular activities

Passion to learn and grow as a candidate

For a complete guide on how to write an entry-level cover letter , check out our guide.

How to Format a Cover Letter?

Here’s what you need to know on how to format a cover letter the right way:

Choose the right cover letter template for your industry . The better fit the cover letter, the less you’ll have to play with the layout and format.

Use colors sparingly . Don’t go overboard with creativity unless you work in an industry where that’s valued (marketing, advertising, design, and the like).

Select professional font styles and sizes.

Set the margins to 1 inch on each side to make sure there is enough white space and the document doesn’t look crowded with text.

Get Inspired with Our Cover Letter Examples

Cover letter templates faq, do i need a different cover letter for every job.

While you don’t need to write a different cover letter from scratch for every single job you apply for, it’s good to tailor your cover letter contents as much as you can to the company and position you’re applying for.

Hiring managers will always go for an applicant who’s interested in their specific position over a candidate that’s sending the same application to dozens of roles.

If you tailor your cover letter to the position, even if it’s something small like addressing the hiring manager by their name or explaining how you possess the right skills for the specific job, your chances of getting hired are going to be much better!

How to Make a Simple Cover Letter for Your Resume?

Simply pick one of our 16 effective cover letter templates above to get started.

We’d recommend matching your cover letter template to the resume template you picked.

Not only will it make your application package look more sophisticated and professional, but it will also make you more memorable for the recruiter who’ll go over your application.

Who Created These Cover Letter Templates?

Novoresume cover letter templates were created in cooperation with professional recruiters and hiring managers.

This means they’re up to date with the latest industry trends and job market requirements. With a Novoresume cover letter template, you can rest assured that your cover letter will look professional and modern at the same time.

When Should I Email My Cover Letter Instead of Using a Template?

As a rule of thumb, it’s always better to use a cover letter template instead of including it in the body of your email as plain text. By using a well-designed and effective cover letter template, you’re guaranteed to look like a more serious and professional candidate.

So, you should only email your cover letter if the job ad specifically asks you to.

Should I Use a PDF or Word Cover Letter Template?

We recommend going for a PDF cover letter template instead of Word.

All types of Operating Systems and devices can open PDF formats without ruining the formatting, design, or layout.

The same, however, cannot be said for Word templates. If, for example, you’ve used a 2021 Word cover letter template and the hiring manager opens it using an MS Word 2016 software version, there’s a chance your formatting will get messed up, or that your font will be unreadable.

To err on the side of caution, we always advise using a PDF cover letter template.

What is the Best Cover Letter Template in 2024?

There’s no such thing as the “best cover letter template.”

After all, every single recruiter has their own personal taste. Some might like a shiny and flashy cover letter template, while others might think it’s tacky. As a rule of thumb, though, we usually recommend customizing each cover letter for the company you’re sending it to.

Do I Really Need a Cover Letter in 2024?

Yes, you definitely need to submit a cover letter with your resume in 2024.

Even if the hiring manager never reads your cover letter or if the job description doesn’t specifically ask for one, a cover letter can still help strengthen your application and make you look like a more serious and proactive candidate.

As such, it’s always a good idea to include a cover letter with your resume.

How to Make a Cover Letter With Novoresume?

To make a cover letter with Novoresume, simply scroll up and pick a template that you like best. Then, register or log in to your Novoresume account. From there, you can add your cover letter contents, as well as personalize and edit them as you see fit.

The Novoresume builder is very intuitive and user-friendly, allowing you to create your cover letter lightning-fast.

To provide a safer experience, the best content and great communication, we use cookies. Learn how we use them for non-authenticated users.

• Resume Templates Simple Professional Modern Creative View all
• Resume Examples Nurse Student Internship Teacher Accountant View all
• Resume Builder
• Cover Letter Templates Simple Professional Modern Creative View all
• Cover Letter Examples Nursing Administrative Assistant Internship Graduate Teacher View all
• Cover Letter Builder
• Cover Letter

Try these Google Docs cover letter templates

1. Spearmint

3. geometric, 4. modern writer, 1. vancouver, 3. amsterdam, 5. santiago.

Google Docs is one of the most popular text editing software and with good reason—this cloud-based service is backed by the world’s leading tech company, meaning Google Docs is reliable, easy to use, and always at your fingertips. 

While you could create your cover letter in Google Docs from scratch, the platform also offers five cover letter templates that allow you to plug in your information and save precious time during your job search. In this blog, we’ll look at all five Google Docs cover letter templates, along with some alternatives if they don’t suit your style. Here’s what we’ll cover:

• Does Google Docs offer cover letter templates?
• The pros and cons of each template: Spearmint, Swiss, Geometric, Modern Writer, and Plum
• Alternative templates to try

How to craft an effective cover letter

About half of hiring managers say a strong cover letter has convinced them to give an interview to a candidate they might have disregarded based on a resume alone. Writing a cover letter is always worth your time!

Source: LinkedIn

What templates does Google Docs offer?

Whether you’re new to Google Docs or have been using it for a while, you may not have noticed that the platform offers a wide variety of templates from reports and brochures to meeting notes and project proposals. For job seekers, the collection of five resume and cover letter templates is particularly useful.

The five cover letter templates currently offered by Google Docs are Spearmint, Swiss, Geometric, Modern Writer, and Plum. You can access them by clicking on “Template Gallery” found on the upper right side of the Docs homepage. Let’s look at the details of each style:

The Spearmint template is the first of the Google Docs cover letter template collection. This template gets its name from the bright green bar at the top of the page which adds a fun pop of color. Below are pre-created sections for your name, your contact information, and the hiring manager’s details. Don’t forget to include the date between the two. The rest of the template is straightforward, with space to address the reader, add several paragraphs of text, and end the cover letter with your name.

• Pros of this template : A fun accent bar that can be adapted to your style preferences. Complements the matching Spearmint resume template.
• Cons of this template : May be too simple for candidates in more creative fields.
• Who we recommend this template for : First-time job seekers, students, hospitality, and customer service professionals.

The second Docs cover letter template is called Swiss and features significantly more creative flair than the first option. This template offers a bold space for your name with your job title in flashy orange below. There’s also space for your details in the left column while the hiring manager’s information goes on the right. The text sits squarely in the center of the page adding extra emphasis and creating a more attention-grabbing layout.

• Pros of this template : Makes a bold statement and features a modern layout. Matches the Swiss Google Docs resume template.
• Cons of this template : The center placement of the text is less reader-friendly and can also make your cover letter appear longer.
• Who we recommend this template for : Creative professionals, artists, photographers, and anyone who needs a touch of design flair for their cover letter.

Geometric is, perhaps, the boldest of the Google Docs cover letter template collection. It features square patterns on both the upper right and the bottom of the page. This design features your name in a bold purple and your contact details in a more subdued gray. The date is listed in pink, followed by light gray text for the hiring manager’s information. There is room for three short paragraphs of text before your signature.

• Pros of this template : A striking design with bold color choices and a unique pattern means your cover letter is sure to stand out.
• Cons of this template : While the text color can be changed, the design colors at the bottom of the page cannot. This template also features less space for writing than others.
• Who we recommend this template for : Sales and marketing professionals, architects, executives, and self-employed people.

Ironically, the fourth Docs cover letter template, named Modern Writer, is not as modern as the name might suggest. Your name is placed in all caps at the top of the page where it’s sure to grab attention. A thick line divides the page before offering room for your personal contact details. The date is set to pink by default, although the color can be changed. There is no space dedicated to the reader’s details. The body of the letter spans across the page and is set to a typewriter-esque font with 1.5-line spacing by default. Besides an all-caps, pink placeholder for your signature, there are no other design details on the page.

• Pros of this template : Simple and draws attention to your name. 1.5-spaced text is easier to read.
• Cons of this template : The two font styles feel mismatched, although they can be updated based on your preferences. There is no place for the reader’s information.
• Who we recommend this template for : Administrative assistants, tech professionals, writers, teachers, academics, and social workers.

The final cover letter template available in Google Docs is called Plum. It’s described as a template for an “informal letter”. The placeholder for your name is a stylized italics font followed by the date. There is no space dedicated for your contact information or the addressee’s details, so you would need to add this information yourself. The greeting is in a larger-than-life font and there’s also a bolded introduction sentence, a feature not found on any of the other templates. This template features plenty of space to write.

• Pros of this template : Offers enough space to contain longer cover letters. Emphasizes the greeting and introduction to capture the reader’s interest.
• Cons of this template : There is no place dedicated to your contact details or the hiring manager’s information—a must for any complete cover letter. Could come across as too informal in certain situations.
• Who we recommend this template for : Marketing, advertising, media, and social media professionals.

Alternative cover letter templates to try

While Google Docs provides a simple framework to begin crafting your cover letter, the template collection may feel limiting for some job seekers. If you’re looking for additional designs, you might want to consider one of the 27 professionally designed templates available in the Resume.io cover letter builder. Here are some of our favorites:

We love this template for many reasons, but one of them is that it’s completely free to use and download! It features a clear header that draws attention to your name and job title, plus space to include all of your contact information. Beneath the elegant dividing line, you can add the hiring manager’s information and find plenty of space to write a compelling cover letter.

How can I create a cover letter for free?

Create a cover letter for free by trying out the Vancouver template inside of Resume.io’s cover letter builder or by using one of the Google Docs templates listed above.

This template is professional and classy, while still making a statement thanks to its subtle left-hand bar that can be edited to a color of your choosing inside of the intuitive cover letter builder. Another strong point of this template is the modern and elegant font style and the ability to download it as either a PDF or DOCX file depending on the employer’s preference.

If you need to make a statement, but color is not an option, Amsterdam is the right template for you. Featuring a bold box for your name and job title along with two clean dividing lines, Amsterdam is sure to make the hiring manager take notice without being over the top.

With a collection of full-page backgrounds to choose from, Rio is almost five different templates in one. Whether you’re into autumn reds, ocean blues, geometric orange patterns, soothing greens, or playful purple, Rio boasts creativity with unique font styles and subtle dividing lines.

Traditional doesn’t need to be boring. As a classic cover letter template, Santiago features a stately font and ample room for your contact details at the top of the page. Below the clean dividing line, you’ll find plenty of room to let your expertise shine as the star of your cover letter.

Is it OK to use a cover letter template?

Cover letter templates are designed to save you time and guesswork when it comes to creating a professional application, so it’s definitely OK to use a cover letter template. However, it’s important to choose a style that reflects your industry and experience level. You should also modify your cover letter template for every job you apply to. A professional cover letter builder can make this easier to accomplish.

Choosing a template is an important first step in creating a professional and convincing cover letter for a job application. Whether you’ve decided to go with a Google Docs cover letter template or an alternate choice, the information on your cover letter should still follow the same basic structure. Here’s what to include:

• Cover letter header . Start by neatly listing your contact details and the date. For an extra strong first impression, use matching cover letter and resume templates for a consistent header look.
• Greeting . Create a personal connection and show that you’re serious about the position by addressing the hiring manager by name. At a larger company, this may not be possible, so make sure the greeting at least contains the company or department name.
• Introduction . Grab the reader’s attention by introducing yourself and your most relevant experience and skills.
• Body . Dive into your relevant experiences, skills, and achievements and show how they align with the employer’s needs based on the job description.
• Conclusion . Wrap up your story by summarizing your qualifications and reiterating your interest in the role. Don’t forget a call to action.
• Signature . End with a professional goodbye, including your name. For letters submitted online, your typed name can serve as your signature.

One easy way to get started writing your cover letter is to look at an example! Check out our collection of free, copyable and adaptable cover letter samples for 300+ job titles.

Key takeaways

Google Docs cover letter templates provide a simple way to get started crafting your cover letter with five different styles to choose from. Each style has pros and cons so make sure to choose the one that is most appropriate for your industry and experience level. If you’re looking for more options, check out Resume.io ’s ever-expanding collection of cover letter samples, with adaptable examples to help you get started. 

No matter which layout you choose, make sure to include your name, contact information, a customized greeting, and a strong body section to make a good first impression and increase your chances of landing the job.

Protect your data

This site uses cookies and related technologies for site operation, and analytics as described in our Privacy Policy . You may choose to consent to our use of these technologies, reject non-essential technologies, or further manage your preferences.

• How Long Should a Job...

How Long Should a Job Interview Last?

5 min read · Updated on September 14, 2022

You want to make a great first impression; there are no do-overs on that, but how long do you have to get that first impression across to the hiring manager or interviewer?

It can be a tough pill to swallow to realize that hours or days of preparation for your interview will amount to only a short period of time in front of the interviewer. The truth of the matter is that interviews aren't supposed to last very long. Obviously, an interview for a full-time job will vary slightly from one for a part-time job, but not by much. 

While there is an average number of minutes that represents a good interview, it's not a set-in-stone timeframe. Interviews can last anywhere between 15 minutes to three hours. Though, if you have an interview that only lasts 15 minutes, that's probably not a good sign. So, how long should you expect a job interview to last?

The 45-minute interview

Forty-five minutes is what is considered the average amount of time a good interview should last. During this time, you'll have the opportunity to talk about your history, skills, education, and achievements while simultaneously sizing up the interviewer and company. 

PRO-TIP: Always remember, you're interviewing them just like they're interviewing you. 

The interview should not be a question-and-answer session. It should be a mutually beneficial conversation about what you bring to the table for them and what they can offer you. That is accomplished by asking them questions , too. 

The 15-minute interview

When you apply for a part-time position, your interview can be fast. It will likely feel like you didn't get enough time. However, if you're applying for a full-time position, a 15-minute interview is not the goal. This short time period simply doesn't provide for effectively relaying what you bring to the table. It often doesn't give you the time to ask them a lot of questions either.

If you realize that your interview is coming to an end and you're near the 15-minute window, try to find out if your qualifications are lacking or if they feel you wouldn't be a fit for the work culture. Qualifications can be augmented with professional development courses. There are even some free certifications you can earn to boost your skills. You can also realign your soft skills so that you will appear to be a better fit during your next interview. 

The 30-minute interview

Thirty minutes is also a good timeframe for an interview. Generally, that's how much time the hiring manager has blocked off to talk with you. Using up all the time on the calendar means that you fully answered their questions. 

The one-hour interview

Most people won't see the one-hour mark very often during interviews. If you make it this far, then you've really piqued their interest. On the other hand, if you're applying for an executive position , one hour should be your goal. 

During this longer interview, you can expect to be asked to meet other people within the company. If you can get the hiring manager out from behind the interview desk, then you're making a very strong impression. You may even be asked to complete an on-site project or efficiency test.

Completing an on-site project or efficiency test

Be careful with on-site projects. Use your judgment about whether they're trying to get free work from you or if they're truly using this step as a means of gauging whether you'll be a good fit for the role. Not to speak ill of any company's interview methods, but there have been occasions when interviewees were asked to work on something during an interview that didn't lead to a callback or job offer. 

Timeframes are similar across interview types

It doesn't matter if you're taking part in an in-person, virtual , or telephone interview, the timeframes mentioned here are a good indicator of whether you'll receive a callback or job offer. The more prepared you are for the interview, the better your chances of being able to manage the time and hit the minute goal you desire. 

Preparation for your interview is critical

Your interview will technically begin when they offer you the time slot. If they call you on the phone, use proper grammar and syntax when you speak because they are listening. This is even more true if the interview offer is by email. Always proofread any written communication. 

Don't forget to research the company to find out what they have going on, more about their products, and pay attention to how the staff is dressed in online photos. Knowing about the company will better enable you to align the answers you provide to their interview questions with the company's goals.

Ultimately, the length of the interview isn't something to stress over too much because 33% of hiring managers make their minds up within the first 90 seconds . This goes back to making a great first impression. If you have a weak handshake, have wrinkles in your pants, or lack confidence, the interviewer loses interest. 

The bottom line is that if you make a great impression and wow them with your abilities, you should hear back from them no matter how much time you spent with them. Before you can share your time with a company during an interview, your resume must be optimized for the job. TopResume has expert writers in every industry that can help you win interviews.

Related reading:

13 Great Interview Questions to Ask a Hiring Manager

7 Free Certification Courses to Enhance Your Resume

5 Ways to Ace the Video Conference Interview   

Phone Interview Coming Up? 5 Ways to Make a Great First Impression

Related Articles:

How to Write a Thank-You Email After Your Second Interview

How to Close the Wage Gap and Earn the Salary You Deserve

Is It an Interview or Not? Interview Tips for Either Way

See how your resume stacks up.

Career Advice Newsletter

Our experts gather the best career & resume tips weekly. Delivered weekly, always free.

Thanks! Career advice is on its way.

Share this article:

Let's stay in touch.

Subscribe today to get job tips and career advice that will come in handy.

Your information is secure. Please read our privacy policy for more information.