useful techniques for giving a presentation

How it works

Transform your enterprise with the scalable mindsets, skills, & behavior change that drive performance.

Explore how BetterUp connects to your core business systems.

We pair AI with the latest in human-centered coaching to drive powerful, lasting learning and behavior change.

Build leaders that accelerate team performance and engagement.

Unlock performance potential at scale with AI-powered curated growth journeys.

Build resilience, well-being and agility to drive performance across your entire enterprise.

Transform your business, starting with your sales leaders.

Unlock business impact from the top with executive coaching.

Foster a culture of inclusion and belonging.

Accelerate the performance and potential of your agencies and employees.

See how innovative organizations use BetterUp to build a thriving workforce.

Discover how BetterUp measurably impacts key business outcomes for organizations like yours.

A demo is the first step to transforming your business. Meet with us to develop a plan for attaining your goals.

• What is coaching?

Learn how 1:1 coaching works, who its for, and if it's right for you.

Accelerate your personal and professional growth with the expert guidance of a BetterUp Coach.

Types of Coaching

Navigate career transitions, accelerate your professional growth, and achieve your career goals with expert coaching.

Enhance your communication skills for better personal and professional relationships, with tailored coaching that focuses on your needs.

Find balance, resilience, and well-being in all areas of your life with holistic coaching designed to empower you.

Discover your perfect match : Take our 5-minute assessment and let us pair you with one of our top Coaches tailored just for you.

Research, expert insights, and resources to develop courageous leaders within your organization.

Best practices, research, and tools to fuel individual and business growth.

View on-demand BetterUp events and learn about upcoming live discussions.

The latest insights and ideas for building a high-performing workplace.

• BetterUp Briefing

The online magazine that helps you understand tomorrow's workforce trends, today.

Innovative research featured in peer-reviewed journals, press, and more.

Founded in 2022 to deepen the understanding of the intersection of well-being, purpose, and performance

We're on a mission to help everyone live with clarity, purpose, and passion.

Join us and create impactful change.

Read the buzz about BetterUp.

Meet the leadership that's passionate about empowering your workforce.

For Business

For Individuals

How to give a good presentation that captivates any audience

Jump to section

What are the main difficulties when giving presentations?

How to create an effective presentation, after that, how do i give a memorable presentation, how to connect with the audience when presenting.

If you’ve ever heard someone give a powerful presentation, you probably remember how it made you feel. Much like a composer, a good speaker knows precisely when each note should strike to captivate their audience’s attention and leave them with a lasting impression.

No one becomes a great public speaker or presenter without practice. And almost everyone can recall a time one of their presentations went badly — that’s a painful part of the learning process.

Whether you’re working within a small creative team or a large organization, public speaking and presentation skills are vital to communicating your ideas. Knowing how to present your vision can help you pitch concepts to clients, present ideas to your team, and develop the confidence to participate in team meetings.

If you have an upcoming presentation on the horizon and feel nervous, that’s normal. Around 15-30% of the general population experience a fear of public speaking . And, unfortunately, social anxiety is on the rise, with a 12% increase in adults over the last 20 years . 

Learning how to give a good presentation can dismantle your fears and break down these barriers, ensuring you’re ready to confidently share your point of view. 

It’s the week before your presentation, and you’re already feeling nervous . Maybe there’ll be an important mentor in the room you need to impress, or you’re looking for an opportunity to show your boss your value. Regardless of your countless past presentations, you still feel nervous. 

Sharing your vision and ideas with any sized group is intimidating. You’re likely worrying about how you’ll perform as a presenter and whether the audience will be interested in what you offer. But nerves aren’t inherently negative — you can actually use this feeling to fuel your preparation.

It’s helpful to identify where your worries are coming from and address your fears. Here are some common concerns when preparing for an upcoming presentation:

Fear of public speaking: When you share your ideas in front of a group, you’re placing yourself in a vulnerable position to be critiqued on your knowledge and communication skills . Maybe you feel confident in your content, but when you think about standing in front of an audience, you feel anxious and your mind goes blank.

It’s also not uncommon to have physical symptoms when presenting . Some people experience nausea and dizziness as the brain releases adrenaline to cope with the potentially stressful situation . Remember to take deep breaths to recenter yourself and be patient, even if you make a mistake.

Losing the audience’s attention: As a presenter, your main focus is to keep your audience engaged. They should feel like they’re learning valuable information or following a story that will improve them in life or business.

Highlight the most exciting pieces of knowledge and ensure you emphasize those points in your presentation. If you feel passionate about your content, it’s more likely that your audience will experience this excitement for themselves and become invested in what you have to say.

Not knowing what content to place on presentation slides: Overloading presentation slides is a fast way to lose your audience’s attention. Your slides should contain only the main talking points and limited text to ensure your audience focuses on what you have to say rather than becoming distracted by the content on your slides.

Discomfort incorporating nonverbal communication: It’s natural to feel stiff and frozen when you’re nervous. But maintaining effective body language helps your audience stay focused on you as you speak and encourages you to relax.

If you struggle to incorporate body language into your presentations, try starting small by making hand gestures toward your slides. If you’re working with a large audience, use different parts of the stage to ensure everyone feels included. 

Each presenter has their own personal brand and style. Some may use humor to break the ice, while others might appeal to the audience’s emotional side through inspiring storytelling. 

Watching online presentations, such as TED talks, is an excellent way to expose yourself to various presentation styles and develop your own. While observing others, you can note how they carry themselves on stage and learn new ways to keep your audience engaged.

Once you’ve addressed what’s causing your fears, it’s time to prepare for a great presentation. Use your past experience as inspiration and aim to outshine your former self by learning from your mistakes and employing new techniques. Here are five presentation tips to help you create a strong presentation and wow your audience:

1. Keep it simple

Simple means something different to everyone.

Before creating your presentation, take note of your intended audience and their knowledge level of your subject. You’ll want your content to be easy for your intended audience to follow.

Say you’re giving a presentation on improving your company’s operational structure. Entry-level workers will likely need a more straightforward overview of the content than C-suite leaders, who have significantly more experience. 

Ask yourself what you want your audience to take away from your presentation and emphasize those important points. Doing this ensures they remember the most vital information rather than less important supporting ideas. Try organizing these concepts into bullet points so viewers can quickly identify critical takeaways.

2. Create a compelling structure

Put yourself in your audience member’s shoes and determine the most compelling way to organize your information. Your presentation should be articulate , cohesive, and logical, and you must be sure to include all necessary supporting evidence to strengthen your main points.

If you give away all of your answers too quickly, your audience could lose interest. And if there isn’t enough supporting information, they could hit a roadblock of confusion. Try developing a compelling story that leads your audience through your thought processes so they can experience the ups and downs alongside you. 

By structuring your presentation to lead up to a final conclusion, you’re more likely to keep listeners’ attention. Once you’ve reached that conclusion, you can offer a Q&A period to put any of their questions or concerns to rest. 

3. Use visual aids

Appealing to various learning styles is a great way to keep everyone on the same page and ensure they absorb your content. Visual aids are necessary for visual learners and make it easier for people to picture your ideas.

Aim to incorporate a mixture of photos, videos, and props to engage your audience and convey your key points. For instance, if you’re giving a presentation on anthropology subject matter, you could show your audience an artifact to help them understand how exciting a discovery must have been. 

If your presentation is long, including a video for your audience to watch is an excellent way to give yourself a break and create new jumping-off points for your speech.

4. Be aware of design techniques and trends

Thanks to cutting-edge technology and tools, you have numerous platforms at your disposal to create a good presentation. But keep in mind that although color, images, and graphics liven things up, they can cause distraction when misused.

  Here are a few standard pointers for incorporating visuals on your slides: 

• Don’t place blocks of small text on a single slide
• Use a minimalistic background instead of a busy one
• Ensure text stands out against the background color
• Only use high-resolution photos
• Maintain a consistent font style and size throughout the presentation
• Don’t overuse transitions and effects

5. Try the 10-20-30 rule

Guy Kawasaki, a prominent venture capitalist and one of the original marketing specialists for Apple, said that the best slideshow presentations are less than 10 slides , last at most 20 minutes, and use a font size of 30. Following this strategy can help you condense your information, eliminate unnecessary ideas, and maintain your audience’s focus more efficiently.

Once you’re confident in creating a memorable presentation, it’s time to learn how to give one. Here are some valuable tips for keeping your audience invested during your talk: 

Tip #1: Tell stories

Sharing an anecdote from your life can improve your credibility and increase your relatability. And when an audience relates to you, they’re more likely to feel connected to who you are as a person and encouraged to give you their full attention, as they would want others to do the same.

Gill Hicks utilized this strategy well when she shared her powerful story, “ I survived a terrorist attack. Here’s what I learned .” In her harrowing tale, Hicks highlights the importance of compassion, unconditional love, and helping those in need.

If you feel uncomfortable sharing personal stories, that’s okay. You can use examples from famous individuals or create a fictional account to demonstrate your ideas.

Tip #2: Make eye contact with the audience

Maintaining eye contact is less intimidating than it sounds. In fact, you don’t have to look your audience members directly in their eyes — you can focus on their foreheads or noses if that’s easier.

Try making eye contact with as many people as possible for 3–5 seconds each. This timing ensures you don’t look away too quickly, making the audience member feel unimportant, or linger too long, making them feel uncomfortable.

If you’re presenting to a large group, direct your focus to each part of the room to ensure no section of the audience feels ignored. 

Tip #3: Work on your stage presence

Although your tone and words are the most impactful part of your presentation, recall that body language keeps your audience engaged. Use these tips to master a professional stage presence:

• Speak with open arms and avoid crossing them
• Keep a reasonable pace and try not to stand still
• Use hand gestures to highlight important information

Tip #4: Start strong

Like watching a movie trailer, the first seconds of your talk are critical for capturing your audience’s attention. How you start your speech sets the tone for the rest of your presentation and tells your audience whether or not they should pay attention. Here are some ways to start your presentation to leave a lasting impression:

• Use a quote from a well-known and likable influential person 
• Ask a rhetorical question to create intrigue
• Start with an anecdote to add context to your talk 
• Spark your audience’s curiosity by involving them in an interactive problem-solving puzzle or riddle

Tip #5: Show your passion

Don’t be afraid of being too enthusiastic. Everyone appreciates a speaker who’s genuinely excited about their field of expertise. 

In “ Grit: The Power of Passion and Perseverance ,” Angela Lee Duckworth discusses the importance of passion in research and delivery. She delivers her presentation excitedly to show the audience how excitement piques interest. 

Tip #6: Plan your delivery

How you decide to deliver your speech will shape your presentation. Will you be preparing a PowerPoint presentation and using a teleprompter? Or are you working within the constraints of the digital world and presenting over Zoom?

The best presentations are conducted by speakers who know their stuff and memorize their content. However, if you find this challenging, try creating notes to use as a safety net in case you lose track.

If you’re presenting online, you can keep notes beside your computer for each slide, highlighting your key points. This ensures you include all the necessary information and follow a logical order.

Tip #7: Practice

Practice doesn’t make perfect — it makes progress. There’s no way of preparing for unforeseen circumstances, but thorough practice means you’ve done everything you can to succeed.

Rehearse your speech in front of a mirror or to a trusted friend or family member. Take any feedback and use it as an opportunity to fine-tune your speech. But remember: who you practice your presentation in front of may differ from your intended audience. Consider their opinions through the lens of them occupying this different position.

Tip #8: Read the room

Whether you’re a keynote speaker at an event or presenting to a small group of clients, knowing how to read the room is vital for keeping your audience happy. Stay flexible and be willing to move on from topics quickly if your listeners are uninterested or displeased with a particular part of your speech.

Tip #9: Breathe

Try taking deep breaths before your presentation to calm your nerves. If you feel rushed, you’re more likely to feel nervous and stumble on your words.

The most important thing to consider when presenting is your audience’s feelings. When you approach your next presentation calmly, you’ll put your audience at ease and encourage them to feel comfortable in your presence.

Tip #10: Provide a call-to-action

When you end your presentation, your audience should feel compelled to take a specific action, whether that’s changing their habits or contacting you for your services.

If you’re presenting to clients, create a handout with key points and contact information so they can get in touch. You should provide your LinkedIn information, email address, and phone number so they have a variety of ways to reach you. 

There’s no one-size-fits-all template for an effective presentation, as your unique audience and subject matter play a role in shaping your speech. As a general rule, though, you should aim to connect with your audience through passion and excitement. Use strong eye contact and body language. Capture their interest through storytelling and their trust through relatability.

Learning how to give a good presentation can feel overwhelming — but remember, practice makes progress. Rehearse your presentation for someone you trust, collect their feedback , and revise. Practicing your presentation skills is helpful for any job, and every challenge is a chance to grow.

Enhance your presentation skills

Discover coaching that transforms your public speaking and boosts your confidence in presenting.

Elizabeth Perry, ACC

Elizabeth Perry is a Coach Community Manager at BetterUp. She uses strategic engagement strategies to cultivate a learning community across a global network of Coaches through in-person and virtual experiences, technology-enabled platforms, and strategic coaching industry partnerships. With over 3 years of coaching experience and a certification in transformative leadership and life coaching from Sofia University, Elizabeth leverages transpersonal psychology expertise to help coaches and clients gain awareness of their behavioral and thought patterns, discover their purpose and passions, and elevate their potential. She is a lifelong student of psychology, personal growth, and human potential as well as an ICF-certified ACC transpersonal life and leadership Coach.

How to write a speech that your audience remembers

6 presentation skills and how to improve them, 3 stand-out professional bio examples to inspire your own, tell a story they can't ignore these 10 tips will teach you how, how to make a presentation interactive and exciting, your guide to what storytelling is and how to be a good storyteller, reading the room gives you an edge — no matter who you're talking to, 18 effective strategies to improve your communication skills, writing an elevator pitch about yourself: a how-to plus tips, similar articles, how to pitch ideas: 8 tips to captivate any audience, the 11 tips that will improve your public speaking skills, 30 presentation feedback examples, fear of public speaking overcome it with these 7 tips, how to not be nervous for a presentation — 13 tips that work (really), stay connected with betterup, get our newsletter, event invites, plus product insights and research..

3100 E 5th Street, Suite 350 Austin, TX 78702

• Platform Overview
• Integrations
• Powered by AI
• BetterUp Lead™
• BetterUp Manage™
• BetterUp Care®
• Sales Performance
• Diversity & Inclusion
• Case Studies
• Why BetterUp?
• About Coaching
• Find your Coach
• Career Coaching
• Communication Coaching
• Life Coaching
• News and Press
• Leadership Team
• Become a BetterUp Coach
• BetterUp Labs
• Center for Purpose & Performance
• Leadership Training
• Business Coaching
• Contact Support
• Contact Sales
• Privacy Policy
• Acceptable Use Policy
• Trust & Security
• Cookie Preferences

We use essential cookies to make Venngage work. By clicking “Accept All Cookies”, you agree to the storing of cookies on your device to enhance site navigation, analyze site usage, and assist in our marketing efforts.

Manage Cookies

Cookies and similar technologies collect certain information about how you’re using our website. Some of them are essential, and without them you wouldn’t be able to use Venngage. But others are optional, and you get to choose whether we use them or not.

Strictly Necessary Cookies

These cookies are always on, as they’re essential for making Venngage work, and making it safe. Without these cookies, services you’ve asked for can’t be provided.

Show cookie providers

• Google Login

Functionality Cookies

These cookies help us provide enhanced functionality and personalisation, and remember your settings. They may be set by us or by third party providers.

Performance Cookies

These cookies help us analyze how many people are using Venngage, where they come from and how they're using it. If you opt out of these cookies, we can’t get feedback to make Venngage better for you and all our users.

• Google Analytics

Targeting Cookies

These cookies are set by our advertising partners to track your activity and show you relevant Venngage ads on other sites as you browse the internet.

• Google Tag Manager
• Infographics
• Daily Infographics
• Popular Templates
• Accessibility
• Graphic Design
• Graphs and Charts
• Data Visualization
• Human Resources
• Beginner Guides

Blog Beginner Guides How To Make a Good Presentation [A Complete Guide]

How To Make a Good Presentation [A Complete Guide]

Written by: Krystle Wong Jul 20, 2023

A top-notch presentation possesses the power to drive action. From winning stakeholders over and conveying a powerful message to securing funding — your secret weapon lies within the realm of creating an effective presentation .  

Being an excellent presenter isn’t confined to the boardroom. Whether you’re delivering a presentation at work, pursuing an academic career, involved in a non-profit organization or even a student, nailing the presentation game is a game-changer.

In this article, I’ll cover the top qualities of compelling presentations and walk you through a step-by-step guide on how to give a good presentation. Here’s a little tip to kick things off: for a headstart, check out Venngage’s collection of free presentation templates . They are fully customizable, and the best part is you don’t need professional design skills to make them shine!

These valuable presentation tips cater to individuals from diverse professional backgrounds, encompassing business professionals, sales and marketing teams, educators, trainers, students, researchers, non-profit organizations, public speakers and presenters. 

No matter your field or role, these tips for presenting will equip you with the skills to deliver effective presentations that leave a lasting impression on any audience.

Click to jump ahead:

What are the 10 qualities of a good presentation?

Step-by-step guide on how to prepare an effective presentation, 9 effective techniques to deliver a memorable presentation, faqs on making a good presentation, how to create a presentation with venngage in 5 steps.

When it comes to giving an engaging presentation that leaves a lasting impression, it’s not just about the content — it’s also about how you deliver it. Wondering what makes a good presentation? Well, the best presentations I’ve seen consistently exhibit these 10 qualities:

1. Clear structure

No one likes to get lost in a maze of information. Organize your thoughts into a logical flow, complete with an introduction, main points and a solid conclusion. A structured presentation helps your audience follow along effortlessly, leaving them with a sense of satisfaction at the end.

Regardless of your presentation style , a quality presentation starts with a clear roadmap. Browse through Venngage’s template library and select a presentation template that aligns with your content and presentation goals. Here’s a good presentation example template with a logical layout that includes sections for the introduction, main points, supporting information and a conclusion: 

2. Engaging opening

Hook your audience right from the start with an attention-grabbing statement, a fascinating question or maybe even a captivating anecdote. Set the stage for a killer presentation!

The opening moments of your presentation hold immense power – check out these 15 ways to start a presentation to set the stage and captivate your audience.

3. Relevant content

Make sure your content aligns with their interests and needs. Your audience is there for a reason, and that’s to get valuable insights. Avoid fluff and get straight to the point, your audience will be genuinely excited.

4. Effective visual aids

Picture this: a slide with walls of text and tiny charts, yawn! Visual aids should be just that—aiding your presentation. Opt for clear and visually appealing slides, engaging images and informative charts that add value and help reinforce your message.

With Venngage, visualizing data takes no effort at all. You can import data from CSV or Google Sheets seamlessly and create stunning charts, graphs and icon stories effortlessly to showcase your data in a captivating and impactful way.

5. Clear and concise communication

Keep your language simple, and avoid jargon or complicated terms. Communicate your ideas clearly, so your audience can easily grasp and retain the information being conveyed. This can prevent confusion and enhance the overall effectiveness of the message. 

6. Engaging delivery

Spice up your presentation with a sprinkle of enthusiasm! Maintain eye contact, use expressive gestures and vary your tone of voice to keep your audience glued to the edge of their seats. A touch of charisma goes a long way!

7. Interaction and audience engagement

Turn your presentation into an interactive experience — encourage questions, foster discussions and maybe even throw in a fun activity. Engaged audiences are more likely to remember and embrace your message.

Transform your slides into an interactive presentation with Venngage’s dynamic features like pop-ups, clickable icons and animated elements. Engage your audience with interactive content that lets them explore and interact with your presentation for a truly immersive experience.

8. Effective storytelling

Who doesn’t love a good story? Weaving relevant anecdotes, case studies or even a personal story into your presentation can captivate your audience and create a lasting impact. Stories build connections and make your message memorable.

A great presentation background is also essential as it sets the tone, creates visual interest and reinforces your message. Enhance the overall aesthetics of your presentation with these 15 presentation background examples and captivate your audience’s attention.

9. Well-timed pacing

Pace your presentation thoughtfully with well-designed presentation slides, neither rushing through nor dragging it out. Respect your audience’s time and ensure you cover all the essential points without losing their interest.

10. Strong conclusion

Last impressions linger! Summarize your main points and leave your audience with a clear takeaway. End your presentation with a bang , a call to action or an inspiring thought that resonates long after the conclusion.

In-person presentations aside, acing a virtual presentation is of paramount importance in today’s digital world. Check out this guide to learn how you can adapt your in-person presentations into virtual presentations . 

Preparing an effective presentation starts with laying a strong foundation that goes beyond just creating slides and notes. One of the quickest and best ways to make a presentation would be with the help of a good presentation software . 

Otherwise, let me walk you to how to prepare for a presentation step by step and unlock the secrets of crafting a professional presentation that sets you apart.

1. Understand the audience and their needs

Before you dive into preparing your masterpiece, take a moment to get to know your target audience. Tailor your presentation to meet their needs and expectations , and you’ll have them hooked from the start!

2. Conduct thorough research on the topic

Time to hit the books (or the internet)! Don’t skimp on the research with your presentation materials — dive deep into the subject matter and gather valuable insights . The more you know, the more confident you’ll feel in delivering your presentation.

3. Organize the content with a clear structure

No one wants to stumble through a chaotic mess of information. Outline your presentation with a clear and logical flow. Start with a captivating introduction, follow up with main points that build on each other and wrap it up with a powerful conclusion that leaves a lasting impression.

Delivering an effective business presentation hinges on captivating your audience, and Venngage’s professionally designed business presentation templates are tailor-made for this purpose. With thoughtfully structured layouts, these templates enhance your message’s clarity and coherence, ensuring a memorable and engaging experience for your audience members.

Don’t want to build your presentation layout from scratch? pick from these 5 foolproof presentation layout ideas that won’t go wrong. 

4. Develop visually appealing and supportive visual aids

Spice up your presentation with eye-catching visuals! Create slides that complement your message, not overshadow it. Remember, a picture is worth a thousand words, but that doesn’t mean you need to overload your slides with text.

Well-chosen designs create a cohesive and professional look, capturing your audience’s attention and enhancing the overall effectiveness of your message. Here’s a list of carefully curated PowerPoint presentation templates and great background graphics that will significantly influence the visual appeal and engagement of your presentation.

5. Practice, practice and practice

Practice makes perfect — rehearse your presentation and arrive early to your presentation to help overcome stage fright. Familiarity with your material will boost your presentation skills and help you handle curveballs with ease.

6. Seek feedback and make necessary adjustments

Don’t be afraid to ask for help and seek feedback from friends and colleagues. Constructive criticism can help you identify blind spots and fine-tune your presentation to perfection.

With Venngage’s real-time collaboration feature , receiving feedback and editing your presentation is a seamless process. Group members can access and work on the presentation simultaneously and edit content side by side in real-time. Changes will be reflected immediately to the entire team, promoting seamless teamwork.

7. Prepare for potential technical or logistical issues

Prepare for the unexpected by checking your equipment, internet connection and any other potential hiccups. If you’re worried that you’ll miss out on any important points, you could always have note cards prepared. Remember to remain focused and rehearse potential answers to anticipated questions.

8. Fine-tune and polish your presentation

As the big day approaches, give your presentation one last shine. Review your talking points, practice how to present a presentation and make any final tweaks. Deep breaths — you’re on the brink of delivering a successful presentation!

In competitive environments, persuasive presentations set individuals and organizations apart. To brush up on your presentation skills, read these guides on how to make a persuasive presentation and tips to presenting effectively . 

Whether you’re an experienced presenter or a novice, the right techniques will let your presentation skills soar to new heights!

From public speaking hacks to interactive elements and storytelling prowess, these 9 effective presentation techniques will empower you to leave a lasting impression on your audience and make your presentations unforgettable.

1. Confidence and positive body language

Positive body language instantly captivates your audience, making them believe in your message as much as you do. Strengthen your stage presence and own that stage like it’s your second home! Stand tall, shoulders back and exude confidence. 

2. Eye contact with the audience

Break down that invisible barrier and connect with your audience through their eyes. Maintaining eye contact when giving a presentation builds trust and shows that you’re present and engaged with them.

3. Effective use of hand gestures and movement

A little movement goes a long way! Emphasize key points with purposeful gestures and don’t be afraid to walk around the stage. Your energy will be contagious!

4. Utilize storytelling techniques

Weave the magic of storytelling into your presentation. Share relatable anecdotes, inspiring success stories or even personal experiences that tug at the heartstrings of your audience. Adjust your pitch, pace and volume to match the emotions and intensity of the story. Varying your speaking voice adds depth and enhances your stage presence.

5. Incorporate multimedia elements

Spice up your presentation with a dash of visual pizzazz! Use slides, images and video clips to add depth and clarity to your message. Just remember, less is more—don’t overwhelm them with information overload. 

Turn your presentations into an interactive party! Involve your audience with questions, polls or group activities. When they actively participate, they become invested in your presentation’s success. Bring your design to life with animated elements. Venngage allows you to apply animations to icons, images and text to create dynamic and engaging visual content.

6. Utilize humor strategically

Laughter is the best medicine—and a fantastic presentation enhancer! A well-placed joke or lighthearted moment can break the ice and create a warm atmosphere , making your audience more receptive to your message.

7. Practice active listening and respond to feedback

Be attentive to your audience’s reactions and feedback. If they have questions or concerns, address them with genuine interest and respect. Your responsiveness builds rapport and shows that you genuinely care about their experience.

8. Apply the 10-20-30 rule

Apply the 10-20-30 presentation rule and keep it short, sweet and impactful! Stick to ten slides, deliver your presentation within 20 minutes and use a 30-point font to ensure clarity and focus. Less is more, and your audience will thank you for it!

9. Implement the 5-5-5 rule

Simplicity is key. Limit each slide to five bullet points, with only five words per bullet point and allow each slide to remain visible for about five seconds. This rule keeps your presentation concise and prevents information overload.

Simple presentations are more engaging because they are easier to follow. Summarize your presentations and keep them simple with Venngage’s gallery of simple presentation templates and ensure that your message is delivered effectively across your audience.

1. How to start a presentation?

To kick off your presentation effectively, begin with an attention-grabbing statement or a powerful quote. Introduce yourself, establish credibility and clearly state the purpose and relevance of your presentation.

2. How to end a presentation?

For a strong conclusion, summarize your talking points and key takeaways. End with a compelling call to action or a thought-provoking question and remember to thank your audience and invite any final questions or interactions.

3. How to make a presentation interactive?

To make your presentation interactive, encourage questions and discussion throughout your talk. Utilize multimedia elements like videos or images and consider including polls, quizzes or group activities to actively involve your audience.

In need of inspiration for your next presentation? I’ve got your back! Pick from these 120+ presentation ideas, topics and examples to get started. 

Creating a stunning presentation with Venngage is a breeze with our user-friendly drag-and-drop editor and professionally designed templates for all your communication needs. 

Here’s how to make a presentation in just 5 simple steps with the help of Venngage:

Step 1: Sign up for Venngage for free using your email, Gmail or Facebook account or simply log in to access your account. 

Step 2: Pick a design from our selection of free presentation templates (they’re all created by our expert in-house designers).

Step 3: Make the template your own by customizing it to fit your content and branding. With Venngage’s intuitive drag-and-drop editor, you can easily modify text, change colors and adjust the layout to create a unique and eye-catching design.

Step 4: Elevate your presentation by incorporating captivating visuals. You can upload your images or choose from Venngage’s vast library of high-quality photos, icons and illustrations. 

Step 5: Upgrade to a premium or business account to export your presentation in PDF and print it for in-person presentations or share it digitally for free!

By following these five simple steps, you’ll have a professionally designed and visually engaging presentation ready in no time. With Venngage’s user-friendly platform, your presentation is sure to make a lasting impression. So, let your creativity flow and get ready to shine in your next presentation!

Discover popular designs

Infographic maker

Brochure maker

White paper online

Newsletter creator

Flyer maker

Timeline maker

Letterhead maker

Mind map maker

Ebook maker

• Google Slides Presentation Design
• Pitch Deck Design
• Powerpoint Redesign
• Other Design Services

• Design Tips
• Guide & How to's
• Presenting techniques

Presenting is a craft that requires a thoughtful approach. There’s a lot of stuff to include in the good presentation. From quality visuals to a compelling speech, everything matters. Doing a presentation on your own may be quite a challenge especially if it’s your first time experience with the presentations. What can really help though, are the effective presentation techniques. In essence, they are the blueprint for your presentation, that helps you to hit all the right spots. Let’s look into some of those techniques.

Presentation Methods

Before you start thinking of a technique, let’s first understand the presentation methods and how they relate to the audience and the content of your presentation. Among the different presentation methods, the main ones are formal and formal. Their difference is mainly in the style of your delivery and the data presentation methods. The formal presentation is best suited for the business meetings or college level, scientific presentations. The informal methods of presentation can best be used during the smaller meetings with your team to discuss business subjects or, for example, at a Ted-like speech event.

Method 1: Keeping Everything Simple

This is a rather basic technique. Just strip your presentation of all the unnecessary information, leaving only the core statements that you want to address. Simplicity not only helps your audience to understand your points better but even more, this data presentation method lowers the risk of making a mistake, forgetting — and saves you and your audience quite a lot of time! There are different definitions of simplicity — sometimes just a few words are enough, while in other cases several bullet points on the slide may be sufficient. Choose what suits your topic best.

Method 2: Good Start 

This method of presentation is all about attention-grabbing. Starting your presentation with a powerful statement, unusual fact or an interesting question will make the audience engage in your presentation instantly. Another great way to start is a joke, though humor can be quite a landmine, especially when you’re presenting in front of strangers, and you are not sure whether your joke would be fun or actually offensive.  So, try to think of something neutral, yet funny.

Method 3: Use  Visuals in your Presentation

Visuals are a must for any presentation and are able not only to support your speech but also to tell and contribute to the stuff you’re telling about. The pictures, graphs, infographics, and even short videos especially when done by presentation design services are what truly make the presentation, and help you to connect with your audience. A carefully selected visual connects both with your speech and the slide content, making your presentation methods work in complete harmony. What is more, visuals can serve as a great way to help you recall your speech in case you suddenly forgot some of it during the presentation.

Method 4:   Rehearse

Don’t rush to tell your presentation just once you’ve made it. Instead, try to first rehearse your presentation in front of a mirror. This presentation technique allows you to spot the mistakes and downfalls in your speech and visual part and improve powerpoint presentation . What is more, it can also make you more confident, as with each time you rehearse you’ll memorize your stuff better and better. Bonus points for starting rehearsing from the random spots in your presentation — using this presentation technique will allow you to become completely familiar with your information.

Method 5:   10/20/30 Presentation Rule

While it may not be applied to all of the presentations, the ones that you are usually dealing with can really benefit from it. 10 20 30 rule is about the time and size of your presentation: 

• Your presentation should have no more than 10 slides
• The time needed for the presentation should be no more than 20 minutes
• The font you are using for presentation text (if there is any on slides) is no less than 30 point

Method 6:  Storytelling

Telling a story is a powerful presentation technique for keeping the audience interested. In general, people get bored from being fed just straight-up facts and numbers for a long time. However, an interesting story, connected to the subject of your presentation gives that personal touch to it, engaging the audience into what you are talking about. What is more, a good story in the context of the presentation will actually resonate with the audience, causing more approval to you as an expert.

• Tell a personal  story .
• Create suspense.
• Bring characters to life.
• Build up to S.T.A.R moment.

Method 7:   Presentate with your Voice

Speech is the most common method of presentation . When you are presenting, it’s important not only WHAT you say, but also HOW do you say it. Creating a proper voice for presentations is actually one of the things you need rehearsal for. Your goal is to sound confident and interested in the subject you are telling about. What is more, it is important to not make unnecessary pauses and avoid the “ummm”, “oh” and other similar stuff that slows down your presentation and may put off the audience.

Method 8:   Know your Audience

Make sure that the data presentation methods you are using make your data  relevant to your audience. The research of your audience is needed to craft a relatable story, as well as to understand what approach in presenting you may want to take. After you’ve done the research, you can just tell the audience what it wants and expects to hear. Such an approach would result in the satisfied and interested audience enjoying your presentation. And in this case your presentation would surely and up being a huge success!

Method 9:   Back up plan

Even though you may plan everything in advance, something can always go wrong. The strange ability of the hardware to malfunction right in the middle of your presentation is probably one of the most known presentation-related memes. So, plan at least some of the bad scenarios. For example, have a printed set of slides with you during your presentation. Check everything right before you’ll start presenting. A good idea also is to have your script written out so that in case you have completely forgotten some of its parts, you can easily and quickly look into it and goon with the presentation.

Method 10:   Relax

This one is not only a presentation technique , but a great life technique as well. Actually, the most common reason for the mistakes during presentations are the nerves and fear a lot of people feel while presenting. It’s absolutely normal to be a little worried about the presentation, but you have to instill confidence in your knowledge and expertise with the subject among the audience, and it’s hard to do if you feel fear. Try to reason with yourself — you have rehearsed, prepared great visuals, learned about the audience and even have a plan B in case the situation gets worse. There’s nothing to worry about — you have all the right presentation techniques !

#ezw_tco-2 .ez-toc-widget-container ul.ez-toc-list li.active::before { background-color: #ededed; } Table of contents

• 50 tips on how to improve PowerPoint presentations in 2022-2023 [Updated]
• Present financial information visually in PowerPoint to drive results
• Keynote VS PowerPoint
• Types of presentations

How to make a presentation interactive

8 rules of effective presentation

How to select and use fonts in PPT

How to make a great presentation

Stressed about an upcoming presentation? These talks are full of helpful tips on how to get up in front of an audience and make a lasting impression.

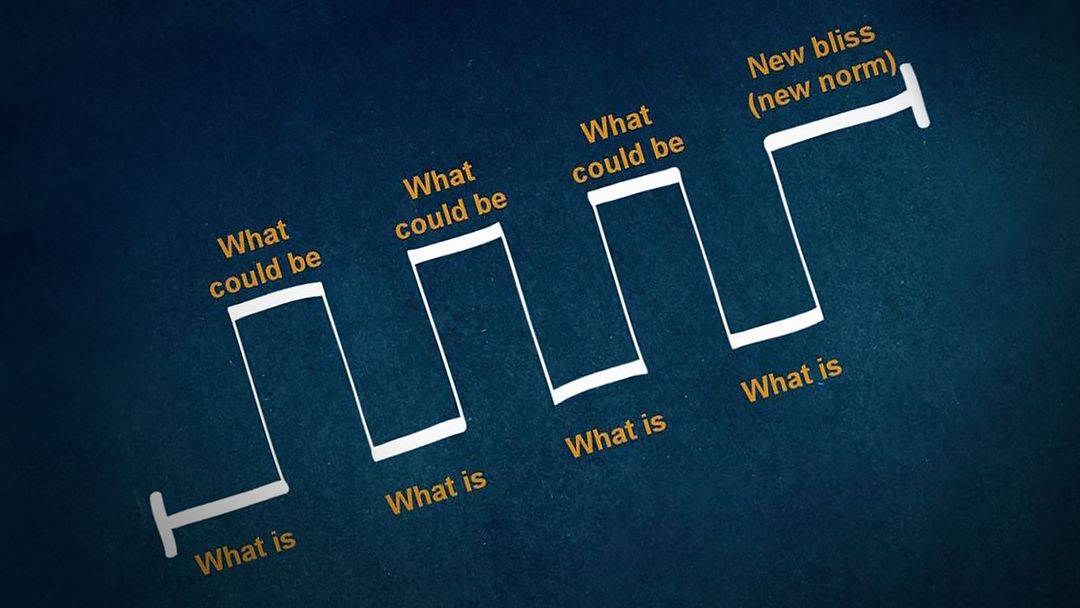
The secret structure of great talks

The beauty of data visualization

TED's secret to great public speaking

How to speak so that people want to listen

How great leaders inspire action

• PRESENTATION SKILLS

Top Tips for Effective Presentations

Search SkillsYouNeed:

Presentation Skills:

• A - Z List of Presentation Skills
• General Presentation Skills
• What is a Presentation?
• Preparing for a Presentation
• Organising the Material
• Writing Your Presentation
• Deciding the Presentation Method
• Managing your Presentation Notes
• Working with Visual Aids
• Presenting Data
• Managing the Event
• Coping with Presentation Nerves
• Dealing with Questions
• How to Build Presentations Like a Consultant
• 7 Qualities of Good Speakers That Can Help You Be More Successful
• Self-Presentation in Presentations
• Specific Presentation Events
• Remote Meetings and Presentations
• Giving a Speech
• Presentations in Interviews
• Presenting to Large Groups and Conferences
• Giving Lectures and Seminars
• Managing a Press Conference
• Attending Public Consultation Meetings
• Managing a Public Consultation Meeting
• Crisis Communications
• Elsewhere on Skills You Need:
• Communication Skills
• Facilitation Skills
• Teams, Groups and Meetings
• Effective Speaking
• Question Types

Subscribe to our FREE newsletter and start improving your life in just 5 minutes a day.

You'll get our 5 free 'One Minute Life Skills' and our weekly newsletter.

We'll never share your email address and you can unsubscribe at any time.

How can you make a good presentation even more effective?

This page draws on published advice from expert presenters around the world, which will help to take your presentations from merely ‘good’ to ‘great’.

By bringing together advice from a wide range of people, the aim is to cover a whole range of areas.

Whether you are an experienced presenter, or just starting out, there should be ideas here to help you to improve.

1. Show your Passion and Connect with your Audience

It’s hard to be relaxed and be yourself when you’re nervous.

But time and again, the great presenters say that the most important thing is to connect with your audience, and the best way to do that is to let your passion for the subject shine through.

Be honest with the audience about what is important to you and why it matters.

Be enthusiastic and honest, and the audience will respond.

2. Focus on your Audience’s Needs

Your presentation needs to be built around what your audience is going to get out of the presentation.

As you prepare the presentation, you always need to bear in mind what the audience needs and wants to know, not what you can tell them.

While you’re giving the presentation, you also need to remain focused on your audience’s response, and react to that.

You need to make it easy for your audience to understand and respond.

3. Keep it Simple: Concentrate on your Core Message

When planning your presentation, you should always keep in mind the question:

What is the key message (or three key points) for my audience to take away?

You should be able to communicate that key message very briefly.

Some experts recommend a 30-second ‘elevator summary’, others that you can write it on the back of a business card, or say it in no more than 15 words.

Whichever rule you choose, the important thing is to keep your core message focused and brief.

And if what you are planning to say doesn’t contribute to that core message, don’t say it.

4. Smile and Make Eye Contact with your Audience

This sounds very easy, but a surprisingly large number of presenters fail to do it.

If you smile and make eye contact, you are building rapport , which helps the audience to connect with you and your subject. It also helps you to feel less nervous, because you are talking to individuals, not to a great mass of unknown people.

To help you with this, make sure that you don’t turn down all the lights so that only the slide screen is visible. Your audience needs to see you as well as your slides.

5. Start Strongly

The beginning of your presentation is crucial. You need to grab your audience’s attention and hold it.

They will give you a few minutes’ grace in which to entertain them, before they start to switch off if you’re dull. So don’t waste that on explaining who you are. Start by entertaining them.

Try a story (see tip 7 below), or an attention-grabbing (but useful) image on a slide.

6. Remember the 10-20-30 Rule for Slideshows

This is a tip from Guy Kawasaki of Apple. He suggests that slideshows should:

• Contain no more than 10 slides;
• Last no more than 20 minutes; and
• Use a font size of no less than 30 point.

This last is particularly important as it stops you trying to put too much information on any one slide. This whole approach avoids the dreaded ‘Death by PowerPoint’.

As a general rule, slides should be the sideshow to you, the presenter. A good set of slides should be no use without the presenter, and they should definitely contain less, rather than more, information, expressed simply.

If you need to provide more information, create a bespoke handout and give it out after your presentation.

7. Tell Stories

Human beings are programmed to respond to stories.

Stories help us to pay attention, and also to remember things. If you can use stories in your presentation, your audience is more likely to engage and to remember your points afterwards. It is a good idea to start with a story, but there is a wider point too: you need your presentation to act like a story.

Think about what story you are trying to tell your audience, and create your presentation to tell it.

Finding The Story Behind Your Presentation

To effectively tell a story, focus on using at least one of the two most basic storytelling mechanics in your presentation:

Focusing On Characters – People have stories; things, data, and objects do not. So ask yourself “who” is directly involved in your topic that you can use as the focal point of your story.

For example, instead of talking about cars (your company’s products), you could focus on specific characters like:

• The drivers the car is intended for – people looking for speed and adventure
• The engineers who went out of their way to design the most cost-effective car imaginable

A Changing Dynamic – A story needs something to change along the way. So ask yourself “What is not as it should be?” and answer with what you are going to do about it (or what you did about it).

For example…

• Did hazardous road conditions inspire you to build a rugged, all-terrain jeep that any family could afford?
• Did a complicated and confusing food labelling system lead you to establish a colour-coded nutritional index so that anybody could easily understand it?

To see 15 more actionable storytelling tips, see Nuts & Bolts Speed Training’s post on Storytelling Tips .

8. Use your Voice Effectively

The spoken word is actually a pretty inefficient means of communication, because it uses only one of your audience’s five senses. That’s why presenters tend to use visual aids, too. But you can help to make the spoken word better by using your voice effectively.

Varying the speed at which you talk, and emphasising changes in pitch and tone all help to make your voice more interesting and hold your audience’s attention.

For more about this, see our page on Effective Speaking .

9. Use your Body Too

It has been estimated that more than three quarters of communication is non-verbal.

That means that as well as your tone of voice, your body language is crucial to getting your message across. Make sure that you are giving the right messages: body language to avoid includes crossed arms, hands held behind your back or in your pockets, and pacing the stage.

Make your gestures open and confident, and move naturally around the stage, and among the audience too, if possible.

10. Relax, Breathe and Enjoy

If you find presenting difficult, it can be hard to be calm and relaxed about doing it.

One option is to start by concentrating on your breathing. Slow it down, and make sure that you’re breathing fully. Make sure that you continue to pause for breath occasionally during your presentation too.

For more ideas, see our page on Coping with Presentation Nerves .

If you can bring yourself to relax, you will almost certainly present better. If you can actually start to enjoy yourself, your audience will respond to that, and engage better. Your presentations will improve exponentially, and so will your confidence. It’s well worth a try.

Improve your Presentation Skills

Follow our guide to boost your presentation skills learning about preparation, delivery, questions and all other aspects of giving effective presentations.

Start with: What is a Presentation?

Continue to: How to Give a Speech Self Presentation

See also: Five Ways You Can Do Visual Marketing on a Budget Can Presentation Science Improve Your Presentation? Typography – It’s All About the Message in Your Slides

.css-1qrtm5m{display:block;margin-bottom:8px;text-transform:uppercase;font-size:14px;line-height:1.5714285714285714;-webkit-letter-spacing:-0.35px;-moz-letter-spacing:-0.35px;-ms-letter-spacing:-0.35px;letter-spacing:-0.35px;font-weight:300;color:#606F7B;}@media (min-width:600px){.css-1qrtm5m{font-size:16px;line-height:1.625;-webkit-letter-spacing:-0.5px;-moz-letter-spacing:-0.5px;-ms-letter-spacing:-0.5px;letter-spacing:-0.5px;}} Best Practices 5 essential preparation steps for a successful presentation

by Tom Rielly • June 15, 2020

Keeping your presentation visuals minimalistic, simple, and clear is just one important step to remember when designing a hit presentation. Leaving nothing to chance, great presenters prove quite methodical as they prepare. Here’s a checklist for everything you need to keep in mind before your next presentation:

1. Choose the right software for your needs

The easiest way to select the right presentation software for you is to simply find the one that is native to your device. For example, if you have a Mac, use Apple Keynote, if you work on Windows, use PowerPoint. Google Slides is recommended if you’re working with someone, as it makes collaboration very easy. Another software option is Prezi: a specialty tool called Prezi that creates a presentation using motion, zoom, and panning across one giant visual space.

2. Organize your files

As you develop your script and visuals, you will need to start assembling all the assets for your slides. Create a unique folder on your computer to hold these items. Keep the folder organized by media type (presentation drafts, photos, videos, scripts) and back them up frequently to the Cloud or external disk. Label each file with a specific descriptive name, e.g. “Susan Johnson singing magpie 2020”, as opposed to “IMG_4043.jpg”, which can make it confusing to find your assets. The more organized you are up front, the easier preparing for your presentation will be.

3. Prepare your presentation materials

Make sure your presentation materials (script, graphics, actual slides) are saved in at least two safe spots (for example, your computer and an external USB drive) and are backed-up frequently. If you are using an online presentation software, such as Google Slides, be sure to also download a copy of your presentation in case the internet connection is unreliable. Having all the individual assets on hand in addition to your presentation slides can be helpful if you experience tech issues before presenting, or if you need to make any last minute changes. Make sure to label your final presentation with the title and your name so it’s easy to find.

4. Practice, practice, practice!

Remember, practice makes perfect. People often run out of time making their presentations and have no time to practice. Most TED speakers practice at least ten times. Neuroscientist Jill-Bolte Taylor gave one of the most successful Talks in TED history with nearly 27 million views. How did she do it? She practiced her Talk over 40 times! By rehearsing multiple times you will naturally memorize your Talk, which means you won’t need note cards when you give your final presentation.

5. Do a final test run

Before presenting, make sure the equipment you need is working properly. It’s generally good practice to rehearse standing on the exact stage with the exact lighting using the exact computer that you will be using in your final presentation.

Here’s a quick checklist of what to look for when testing your equipment:

• If you're not using your own computer, the one provided might be slower and have trouble playing media. If you have videos or other media, make sure they play correctly
• Test the projector to make sure it’s HD
• Make sure images are clear
• Test the sound of any clips you use, as this is what goes wrong most frequently
• If you’re using a mic, test the volume

Don’t let technical issues or other blunders overshadow your presentation. By following these guidelines, and with a little preparation, you can engineer out the problems BEFORE they happen.

Ready to learn more about how to make your presentation even better? Get TED Masterclass and develop your ideas into TED-style talks

© 2024 TED Conferences, LLC. All rights reserved. Please note that the TED Talks Usage policy does not apply to this content and is not subject to our creative commons license.

20 Presentation Tips to Keep Your Audience Engaged from Start to Finish

Business | Marketing | Nonprofits | Students | Teachers

By kai tomboc - january 14, 2020.

Losing the audience’s attention is one of the most painful challenges for anyone making a presentation.

Halfway through your presentation, you notice that a couple of audience members are getting restless. The people at the back seem bored as they look down on their phones, and one of them just yawned (ugh!).

You start to feel that you failed to engage your audience. You wonder if you’re the problem. Are you a boring presenter? Perhaps you’re stuffing too much information in your slides.

Master audience engagement with these presentation best practices

From engaging product demos to presentation decks that stand out, read on for 20 valuable tips to keep your audience excited to hear more from you.

What makes a great presentation?

Before you get started, it pays to know what makes an excellent presentation.

1. It informs your audience by providing reliable information.

People want to be informed. They want to learn something new. For this reason, you should look for reputable links. The information should be as recent as possible, and at least less than a year old.

Your research work doesn’t need to be from online sources. You could also cite printed sources from the library. Double-check all of your sources and make sure they have substantial research and statistics to back them up.

2. It persuades your audience to take action.

A presentation should be persuasive. This is especially true for business presentations and product demos. You might also want to appeal to your readers through emotions.

3. It educates your audience and empowers them to make informed decisions.

Presentations are, by nature, educational. You might be introducing your audience to a new idea, product, or service.

4. It instructs your audience in a clear, compelling way.

A presentation should be instructional. Organize your presentation as clear and concise as possible, so your audience will be able to digest your information more effectively.

5. It inspires your audience by being memorable.

A good presentation motivates an audience to act on things that they’ve been meaning to do after hearing you speak or present.

20 best pactices for visually-appealing, convincing presentations

With all that in mind, here’s a list of useful best practices and tips for presentations that stick.

1. Know your target audience.

Your target audience is the demographic that you’re aiming to convince, educate, or inspire with your presentation. This crucial step helps you craft a presentation that resonates with your intended audience.

For instance, if you’d like to educate teens, create a presentation that appeals to their age group. Make your presentation more upbeat, and use pop culture references and images that they can relate to.

On the other hand, if your target audience spans middle-aged professionals, your presentation should be straight-to-the-point and based on facts. These professionals are typically results-oriented, and they want to get to the heart of the matter right away.

By and large, getting to know your target audience enables you to create a presentation without wasting time on uninterested demographics.

2. Create an outline.

Your next step is to create an outline of your presentation. It will help ensure order in your presentation and present facts and sources as effectively and efficiently possible.

It’ll also help if you assign a subtopic for each slide. Let’s say your main topic is the American Civil War. The war lasted roughly four years, and if you delve into it without any organizational structure, your audience will end up confused. Sort your slides according to year and the important events that took place. The same applies to any topic.

3. Start with a memorable introduction.

Opening a presentation with “My name is .. ” or “I’m here to talk about..” are less likely to make your presentation memorable and engaging to your audience.

So how do you keep everyone glued to your presentation with a powerful, memorable opener?

Share an anecdote, ask an intriguing question, or get people’s energy up with a short activity.

Next, make your opening slides as eye-catching as possible. In your opening slide, use bold fonts. Add visuals like gifs or an animated infographic.

Finally, provide an overview of your presentation in the introduction slide. An overview that meets your audience’s expectations of your presentation helps keep an audience absorbed and attentive from start to finish.

4. Eliminate clutter in your slides.

Avoid overcrowding your slides with images or graphics. Although it’s fine to use visuals to complement your slides, the keyword here is “complement.”

Too many photos will make your slides look cramped. Take a minimalist approach to your slides. For images and graphics, use them sparingly and thoughtfully.

Don’t be afraid of white space in your slides. Consider readability first, visual appeal second.

5. Use pictograms.

Lengthy presentations could get boring in the long run. So if you want to keep your audience’s attention, you will need to make your presentation attractive and easier to understand.

Enter pictograms !

Pictograms express information, ideas, or messages through images, signs, or symbols. Also, they can help simplify complicated concepts.

6. Be thoughtful of your color scheme.  

Your choice of colors can have an impact on your audience’s mood and perception of your presentation. It may not be evident at first glance, but your presentation colors can draw a particular set of feelings from your audience. Orange looks more carefree than beige, right?

Here are some quick tips to help you pick the right color combination for your presentation:

• Choose a color scheme that matches your presentation’s theme. For example, if you’re about to present a serious topic, consider somber, dignified colors like white, black, or brown. But if you want your presentation to be more upbeat, use lighter hues like yellow and orange. 
•  Use your brand colors to raise brand awareness and recognition. 
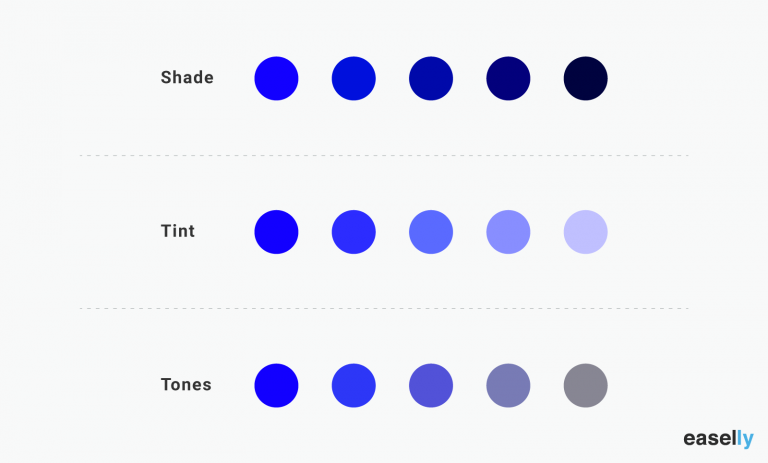
• Stick to 2-3 colors. Joint research by Adobe and the University of Toronto revealed that most people prefer a combination of 2-3 colors. A good rule of thumb is not to use more than four colors. When using more than 3-4 colors, go for shades, tones, and tints of your original colors like the example below.

7. Focus your audience’s attention using data visualization.

Presenting statistics and percentages in writing can be a challenge to use in your presentation. For this reason, consider data visualization.

For example, graphs and charts are often used to highlight comparisons in data. You can also use them to inform your audience of a specific data point.

It’s worth noting that a poorly-designed graph or chart could ruin your presentation if proven false or shabbily done. Make sure that your data are correct, and your diagrams or charts are correctly labeled. Don’t just use pie charts because they look hip and smart. You have to learn how to choose the right chart or graph to visualize your data.

8. Use presentation templates.

Templates often take a bad rap because they’re perceived as limiting, sapping one of creative freedom. However, templates shouldn’t be perceived this way.

Think of templates as frameworks or a set of building blocks that you can tinker with as you create your presentation. Without a templated structure, you’ll likely waste a lot of time and resources making your presentation from scratch.

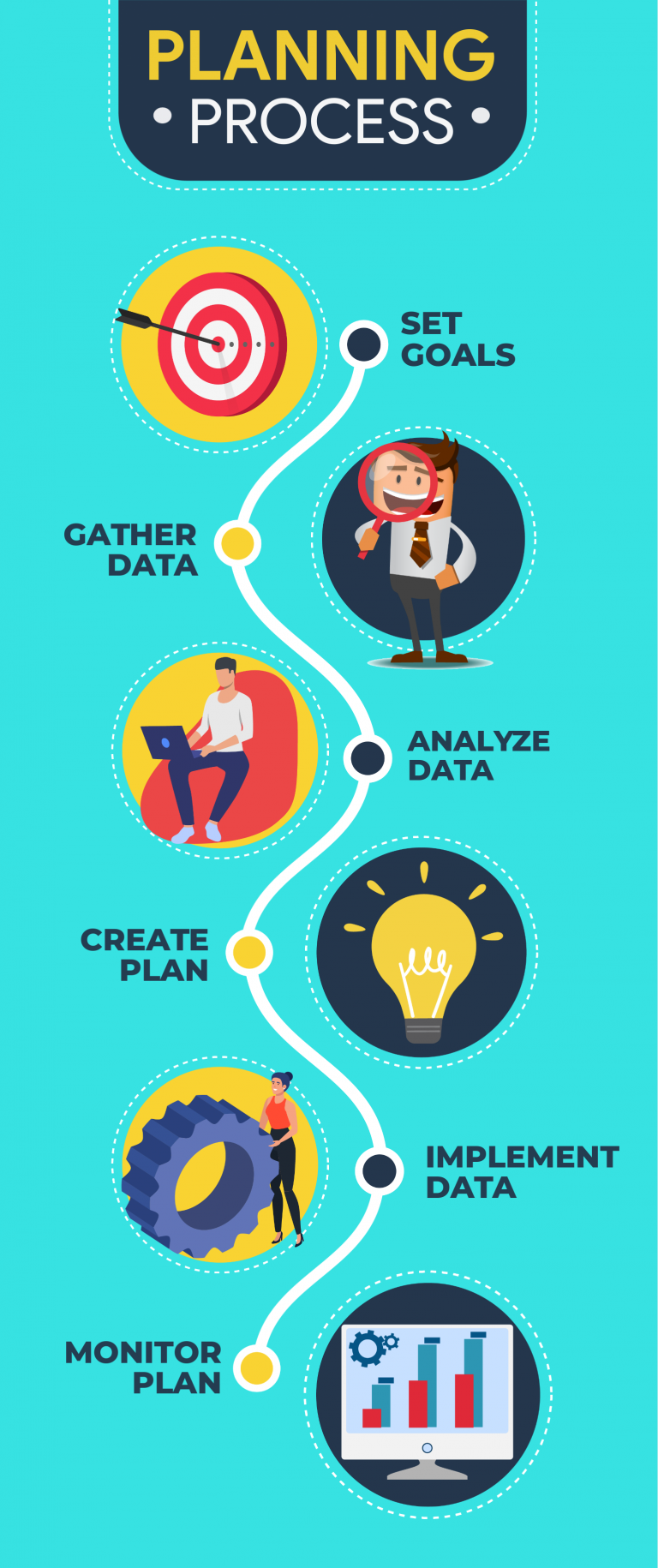
For example, use infographic templates as a way to make your presentation more engaging (minus the time-consuming task of making a presentation from scratch. The process infographic template below is perfect if you’re explaining a process in one of your presentations.

9. Try the duotone effect in your presentations.

The duotone effect is the use of two contrasting colors to create dramatic, visually pleasing results. Thus the name duotone.

This design style is gaining popularity with designers and non-designers alike. Learn more from this quick duotone tutorial via Adobe .

10. Show, don’t tell.

Stories are a powerful medium to get your audience to sit up and listen to you. For this reason, aim to “show” rather than “tell” your audience about a topic, insight, or idea.

For example, don’t just state facts or figures about the dangers of not investing in their retirement. Instead, share the story of someone you know who failed to plan for their retirement, nudging your audience towards making their own conclusions or insights.

Don’t bombard your audience with too much information all at once. Avoid jargon or complex concepts without sharing a story that’ll resonate with them. With compelling storytelling, you can create anticipation and then slowly build up to your key points.

11. Incorporate infographics into your presentation.

Infographics are valuable presentation tools because they combine visuals and text. As a result, you can communicate with impact.

Furthermore, infographics make your presentation more memorable. How?

A relevant image paired with informative text helps people retain 65 percent of the information three days later — a stark contrast to presenting text-only content where someone’s likely to remember only 10 percent of the information.

Here are a few guides and tutorials when creating infographics for your next presentation:

• Guide to Making Infographics from Scratch (guide)
• 5 Ways to Use Call to Action in Your Infographic to Boost Audience Engagement (video)
• How to Write Sharp, Compelling Infographic Copy (guide)

Easelly Pro Tip: Divide long infographics into smaller segments. Add an infographic section for each presentation slide. If you’d like to raise the bar further for your presentation, try animated infographics to make your slides come to life.

12. Avoid using bullet points.

Bullet points are great tools to emphasize tips, features, or steps in lists. However, it’s best to avoid them in presentations because they don’t help your audience retain information.

Research even supports this recommendation. In 2014, the International Journal of Business Communication published the results of their research —   The Use of Visualization in the Communication of Business Strategies: An Experimental Evaluation .

The researchers wanted to learn whether the use of visuals is superior to text (a bulleted list to be specific) in communicating the strategy of the financial services branch of an international car manufacturer.

The researchers concluded the following:

“Subjects who were exposed to a graphic representation of the strategy paid significantly more attention to, agreed more with, and better recalled the strategy than did subjects who saw a (textually identical) bulleted list version.”

Instead of using bullet points, consider using icons or visuals.

Take a look at the example below. Which do you think will likely get the audience’s attention and be more memorable after the presentation?

13. Choose fonts that are easier to read.

The quality of your font could affect your audience’s reaction to your presentation. Don’t just use the first standard font that pops up in your presentation editor.

Your font should match the mood and intent of your presentation. If you want your presentation to appear casual, choose a font that gives off a similar feeling.

14. Use contrast in your presentation.

Check for contrast between your texts and presentation background to ensure readability. Make it a point to distinguish one from the other.

It’s also worth noting that you are going to show your presentation to a group of people. Depending on the seating arrangement, viewers at the back may find it hard to read your presentation. Make sure that your fonts are of the appropriate size. That way, none of your audience members will have to struggle reading your slides.

15. Consider gifs and memes

Gifs and memes are popular media tools for a good reason. You could incorporate them into your presentation, and they could add a sense of humor to your topic or pitch.

When using gifs and memes, avoid those that could be misinterpreted as politically incorrect or culturally insensitive.

16. Create a consistent look and feel in your slides.

Choose a theme for your presentation templates, and stick with it ’til the end.

This doesn’t mean that you should be boring or dull with your presentation. You can add images and infographics, but there should be a sense of consistency in your slides.

Consistency leads to familiarity, which in turn encourages learning and engagement.

17. Ask intriguing questions.

Asking intriguing questions enables you to draw your audience’s attention and highlight key points at the same time.

For example, you are conducting a presentation on the Roman empire. You want to get your audience’s attention, so you raise questions such as what they know about the Roman empire, and how did the Roman empire impact modern society?

The audience may or may not get the right answers, but they will most likely try their best to answer your questions. The resulting exchange of ideas will make your presentation more spontaneous and engaging.

18. Limit to one visual per slide.

Using too many visuals at once will make your presentation appear cluttered. Limit to one visual per slide to help your audience engage more with your text and information.

19. Embrace white space.

White space , also known as negative space, is the space between the lines of texts and visuals in your presentation.  It doesn’t have to be  white  as it can also take the color of your presentation’s background. Think of white space as “empty space”. 

It helps improves readability and ensures that your graphics and texts are clear and legible in your presentation. 

20. End your presentation with an excellent call-to-action.

Call-to-action statements are an integral part of any presentation. They compel your audience to take action, and it makes your presentation more interactive.

Here’s a short video explaining how to use call-to-action in infographics (the same principles apply for presentations!):

Say you’re designing a presentation for a new gym you’re managing. You want people to try out the gym and the services you offer. You could incorporate the call to action at the end of your presentation.

“See you at the gym next week?” or “Level up in the New Year by signing up for our free gym membership for a month!” are good call-to-action statements that you can use.

Ready to start creating your presentation?

We’ve got your back if you need help with your visuals and infographics for your next presentation.

Use our simple infographic maker tool or hire one of our infographic design pros for custom infographics and animated infographics .

Here’s to a stellar presentation – we’re rooting for you!

More to learn from the blog…

How to collect your own data: an interview with max galka (part 2).

As we mentioned in Part 1 of our interview with Max Galka, data visualization has become one of the biggest trends of 2016. Not only do we ...

Deliver the Perfect Presentation with Infographics as Visual Aids

Visual aids are more than just eye candy. Whether it’s for a school report or a business conference, visual aids are a great entryway ...

What is Information Design and Why It Matters Now More Than Ever

Have you ever found yourself squinting hard while reading too small instructions in your coffee maker manual? Or have you had problems fill...

• Presentations
• Most Recent
• Infographics
• Data Visualizations
• Forms and Surveys
• Video & Animation
• Case Studies
• Design for Business
• Digital Marketing
• Design Inspiration
• Visual Thinking
• Product Updates
• Visme Webinars
• Artificial Intelligence

15 Expert Tips for Giving a Powerful Business Presentation

Written by: Mahnoor Sheikh

A powerful business presentation is much more than just a bunch of nice-looking slides.

Whether you’re presenting to venture capitalists, senior management or potential customers, you need to make a great first impression and stand out from the dozens of other speakers they’ll encounter.

For some people, presenting in front of even a handful of listeners can be a nightmare. And when it's a room full of important business folks, like investors or your boss, things get even worse.

If that sounds like you, don't worry. We have a way to calm your nerves and bring back your confidence.

In this post, you'll find 15 expert tips to help you deliver an unforgettable business presentation.

Ready to create your business presentation? Our presentation maker can help you create a professional slide deck quickly and easily using ready-made templates.

1 Know your material.

Before you can convince anyone else, you need to be completely sold on your idea or product. It’s important that you know the points you are making, inside and out.

When you present before an audience, you’ll likely be using visual aids, notes and/or slides. While these tools can help, make sure they aren’t the sum of your expertise.

These are only tools to aid you in your ability to communicate.

Don't rely on them too much or you’ll come across as unsure and boring. Your knowledge of your subject should be beyond your cue-cards so that you can effectively answer any questions that crop up.

You need to inspire confidence. If you bring up a point that is on your slide, back it up with statistics that you’ve encountered or quotes that relate to your topic.

2 Be enthusiastic.

Believe me, vibes matter.

No one wants to hear you drone on about a subject you don’t care for. If you’re tired and bored of your own presentation, your audience is probably feeling the same way.

Anyone listening to you should know how passionate you are about the subject. This will be very apparent in your body language , like the way you speak, make eye contact and walk around on the stage.

Harvard professor Amy Cuddy studies how body postures can communicate power.

Before her highly successful TED talk, she spent time striding, standing tall and extending her body. These movements got her into the zone of feeling powerful and passionate.

It’s also important that you properly energize yourself before a business presentation.

Do some warm-up exercises, like stretching or vocal exercises.

Check out this video on vocal exercises to practice before an important speech or presentation:

You can also do other things that get you focused and energized. Go through inspirational quotes or listen to music. Make sure you’ve drunk enough water and keep a bottle with you during your presentation.

3 Arrive early to set up.

One of the things that can mess up your business presentation is not being familiar with the space you’ll be speaking in. Make sure you arrive at your venue at least an hour in advance.

Set up anything you’ll need , like a projector, laptop or speakers.

If the venue already has all the equipment set up, make sure everything is compatible and working fine. Transfer any files from your USB or download them off of your email or cloud.

Next, check if there are any impediments to your being heard or seen.

Sit at different locations in the audience area to make sure the stage is visible, and the speaker can be heard at the very back. This will help you assess how loud you should be.

Check to see if the projection is visible in the lighting you have, and adjust the lights accordingly.

Another big advantage of arriving early is that you get to meet and greet some of your audience members. This will help you feel more confident on stage as you’ve already broken some of the ice .

Hey executives! Looking to cut design costs?

• Spend less time on presentations and more time strategizing
• Ensure your brand looks and feels visually consistent across all your organization's documents
• Impress clients and stakeholders with boardroom ready presentations

Sign up. It’s free.

4 Be comfortable with your own self.

You’ve prepped well, you know your stuff inside-out and your visual aids are ready. The next big questions are: What should you wear? How should you act?

It can be tricky deciding what to wear to give a killer business presentation, but your look will likely depend upon your comfort and who your audience is.

Lauren McGoodwin, founder and CEO of Career Contessa, recommends :

“When dressing for a presentation, it’s important to wear something you’re comfortable in, and something that makes you feel confident.”

She also says that you should wear something that allows you to move and gesture freely.

But regardless of what you wear, it’s important to be your best self.

Many people are nervous speaking in front of an audience, so rehearse beforehand and have a friend, colleague or any objective observer monitor you.

If you come across as jittery—always shifting your weight from one leg to another, moving your hands too much, shaking, etc—it’s a good idea to take a note of all that and work at establishing a firm presence on stage before your big day.

How you act also depends upon your personality.

Adopt your natural position. If you’re comfortable standing in place, don’t force yourself to stride across the stage. If your voice is gentle, no need to yell, just get a microphone.

Keep your everyday demeanor and bring out the best you.

5 Open strong.

We live in an era where audiences have low attention spans and expect to be entertained. Start your business presentation with a bang so as to set the tone for the rest of your presentation.

You could start off with a statistic that shocks the audience into sitting up and taking note or with a quote that instantly makes them listen.

Don’t forget to put them at ease by reassuring them: “I know you may be wondering…”, “…that fact may seem shocking, but research backs it up because…” etc.

You could also start with an interesting image , an attention-grabbing video or a touching personal story.

Remember, first impressions are everything.

You need to convey to your audience that your business presentation will be worth their while and not just a run-of-the-mill lecture where you dispiritedly talk at them.

6 Set goals for your business presentation.

At the very beginning of your presentation, lay out the goals you hope to meet during your time on stage. This tells the audience why they should listen to you and what they have to gain from paying attention.

As these goals are met, both you and your audience will feel a sense of purpose and achievement at effective communication. Here's a customizable presentation slide template in Visme for goals.

Ready to create your own business presentation?

• Add your own text, images, colors and more
• Choose from hundreds of slide designs and templates
• Add interactive buttons and animations

Your audience will be more likely to remain tuned in if they can see the objectives of the presentation being fulfilled and this in turn will make them more likely to deem your talk a ‘success’.

These goals will also help your audience remember crucial points of your business presentation, which will ensure that you have a productive Q&A session.

7 Tell a story.

Stories connect with people much more than statistics, academic points or even quotations do.

A story can be personal, of course, but it can also be the story of a brand or even a story about consumers.

Steve Jobs was a great corporate storyteller and he shone at every Apple product launch presentation. Check out this video of Jobs presenting at the launch of the iPhone in 2007.

Steve Jobs framed his company’s new innovations in terms of stories of revolution. Macintosh “changed the whole computer industry” and the iPod “changed the whole music industry”.

These were stories of change that brought the product, the consumer, and the exciting time they were living in all together—it made the audience go on a journey.

You can work in a similar way by highlighting the problems (the villain) and how your product, business or idea (the hero) will lead your audience closer to a solution. Telling stories can make your business seem like part of a grand narrative that your audience wants to become a part of.

Then, of course, there are personal stories. These usually appear at the beginning, but a good presentation makes effective use of them throughout.

Tell your audience how you got to where you are, and what makes you believe in your business.

Remember to keep it short, but interesting.

The goal is to establish an emotional connection with your audience so your message hits home. Don’t overdo it or deviate from your actual point.

If you’re looking for more storytelling techniques to incorporate into your presentation, check out this Visme video on presentation structures used by top TED speakers:

8 Interact with your audience.

A business presentation can get boring and sleep-inducing real fast if you just talk “at” your audience instead of talking to them.

Turn your presentation into a conversation by involving your audience in the discussion. Ask them questions, take their feedback and connect with them via anecdotes (“I know we’ve all felt this way”.)

You can also get them to sit up and work with you. For example, they could be asked to raise their hands if they agree during certain points of the presentation.

Interacting with your audience during your business presentation will help prevent the dreaded “ death by PowerPoint ” and keep them wide awake and attentive.

9 Use visual aids.

Visuals help people retain information for longer periods of time, so use them generously throughout your presentation to make sure your message hits home.

And no, visual aids don’t necessarily mean boring PowerPoint slides.

Pictures, videos and art are also great mediums to get your points across and intrigue the audience. Visual flowcharts can help summarize complex topics.

And if you really do want to use presentation slides, use a tool like Visme to create ones that look professional and stand out from the rest. Check out these editable business presentation templates .

Use data visualization, like bar graphs, pie charts and more to make numbers look interesting.

Visme lets you create over 15 different types of graphs and tons of data widgets, like progress bars and radials, for your business presentation. You can also tap into the flowchart maker, array maker, map engine and other tools to help you visualize information. Here's a sneak peek at how it works:

As for the slides, make sure you don’t stuff them with text.

If you put bullets up on the screen, make sure they are visible and condensed. No one wants to see entire paragraphs up there when you’re talking to them at the same time.

A quote or two is fine, but don’t overdo it.

10 Add some business-friendly humor.

During long presentations, there is nothing more relaxing than a speaker who can make you laugh.

If you just keep talking in a serious tone, it’ll seem like you’re droning on. A friendly, conversational style and light jokes can make sure that you retain your audience’s attention.

But remember, this is a business presentation. Don’t go overboard with comedy or your audience won’t take you or your presentation seriously.

We recommend using humor only if you’re naturally good at. If not, don’t force it.

11 Make startling statements.

Every once in a while, shock your audience into sitting up and focusing.

Challenge their existing beliefs with solid knowledge and statistics. While a startling fact or statistic can be a great way to begin a presentation, it is also important to use these statements throughout.

Don't overdo it so it loses its appeal, but around thrice during an hour-long presentation should be good.

12 Remember the 10-20-30 rule.

Venture capitalist Guy Kawasaki came up with this handy presentation rule in 2005 .

Here’s an infographic that sums it up:

Want to create your own stunning infographic in minutes?

• Choose from dozens of professionally designed templates
• Add and alter icons, colors, fonts, images and more
• Customize anything to fit your brand image and content needs

Kawasaki sat through many, many bad presentations and figured out this rule to make sure presentations stop being so repetitive and boring.

10 slides give presenters an ample amount of space to summarize their argument. Any more information and the audience is likely to lose focus and doze off.

20 minutes is how long the average person can pay attention without losing his mind wandering. Kawasaki says that, in an ideal world, the last 40 minutes of the presenter’s hour will be utilized in a Q&A session.

A font size of 30 points means that everyone can read a presentation, even from the back of the room, and the presenter is forced to put minimal text up on the screen.

Keep in mind that Kawasaki is talking about a specific situation, a pitch for a room full of venture capitalists.

While his points can be generalized, a business owner may also find themselves in a situation where they aren’t perfectly applicable. It would be good to revise them slightly in different situations.

13 Make eye contact and smile.

You don’t have to stand there and speak like a machine. Your audience will respond better to the presentation if you personalize your interactions with them.

Make sure you meet the eyes of multiple members of the audience so that they feel like you are paying attention to them individually.

Eye contact can reassure your audience that you value their time and are grateful for their presence and it can also drive home the message that you are confident in your pitch.

Smile at audience members when you meet their eyes! If you’re nervous, locate five or six friendly faces in the crowd and keep coming back to them for encouragement.

14 Be prepared for tough questions.

Don’t underestimate the power of the Q&A session!

Your answers can make or break your business presentation. A good presenter knows their material completely and is ready to face difficult questions.

Here's an editable presentation slide template in Visme for Q&A sessions:

Remember, people will trust in you and your business venture if they are sure you know what you’re doing.

If you’ve ended your presentation on an awkward silence, ask some questions yourself and use language that makes it apparent that you know the concerns of your audience.

Start with phrases like “Now, you may be wondering if…”. This sets the crowd at ease and allows them to comfortably voice their concerns.

15 Close on a high.

It is very important to have a closing note after the Q&A session. You shouldn’t need a slide for this part, but you can use one if you want.

The way you conclude your presentation should be powerful and ensure that the audience remembers you. Like your opening, you can end with a personal story or quotation. Or remind them about the goals and summarize the main points quickly.

Make sure the end is euphoric and shows that your ideas can achieve success. This will ensure that your listeners place their confidence in you and leave feeling satisfied and uplifted.

Make Your Business Presentation a Success

The secret to giving a successful business presentation is putting your heart and soul into connecting with your audience and truly showing them the value in your ideas.

This list of professional tips can empower you in small ways, leading to big outcomes.

If you’re already feeling pumped about your next business presentation, create one that doubles your impact using Visme’s presentation maker .

Sign up for a free account today and take it for a test drive!

What do you struggle with the most when it comes to giving business presentations? Let us know your thoughts, questions and feedback in the comments below.

Create beautiful presentations faster with Visme.

Trusted by leading brands

Recommended content for you:

Create Stunning Content!

Design visual brand experiences for your business whether you are a seasoned designer or a total novice.

About the Author

Mahnoor Sheikh is the content marketing manager at Visme. She has years of experience in content strategy and execution, SEO copywriting and graphic design. She is also the founder of MASH Content and is passionate about tea, kittens and traveling with her husband. Get in touch with her on LinkedIn .

10 Tips for Giving a Great Presentation in English

• September 15, 2014

Giving the perfect oral presentation in English requires practice. Remember that even great orators like Steve Jobs, Abraham Lincoln, Nelson Mandela and Martin Luther King became excellent public speakers through years of dedicated practice.

When preparing your presentation in English, we recommend you watching and listening to the recordings of their public speeches as an example. Check out our video lesson and some other useful tips for giving a great presentation below.

1. Think About the Details in Advance

Giving a presentation in front of an audience is always stressful. Thinking about such details as the location of the presentation, equipment, materials, timing, your appearance and outfit will help you avoid nervousness.

2. Do Your Homework

Effective preparation requires consideration of the following things:

• Ask yourself what the presentation is all about, its title and its goal
• Think about who your audience is
• Figure out what your main message is
• Think about the structure of the presentation: the opening, the main part and the summary
• Make it easier for the audience and yourself: use simple language
• Prepare yourself for questions. Think about what questions the audience might ask
• Usually an orator has a maximum of 15 minutes to present. So, make the presentation simple, have no more than 20 slides using a font that is legible from a distance
• Don’t put large blocks of text in your presentation. No one will be interested in reading it; people prefer visual material. So think about images, graphs and videos that support your idea, but don’t overwhelm the audience with too many visual aids

3. Introduce Yourself and Set the Theme

At the beginning of the presentation, it’s important to introduce yourself, giving your full name, position and company you represent. Some people also include their contact information on the first slide. That’s in case you want someone from the audience to contact you after your presentation. After the introduction, don’t forget to state the topic of your presentation.

Useful phrases in English:

“Hello, ladies and gentlemen, thank you for coming…” “The topic of today’s meeting is…” “Let’s get the ball rolling” “Shall we get started?”

4. Provide an Outline or Agenda of Your Presentation

Providing an outline of the presentation is a must, as people want to know why they should listen to you. That’s why the opening part is very important. It should be cheerful, interesting and catchy. You should know it by heart, so you don’t lose track of your thoughts even if you are nervous.

“I’d like to give you a brief outline of my presentation…” “Here is the agenda for the meeting…” “My presentation consists of the following parts…” “The presentation is divided into four main sections…” 5. Explain When the Listeners Can Ask Questions

A Question & Answer period (Q&A) usually takes place at the end of the presentation, so you have enough time to deliver the main message of your speech without being interrupted by multiple questions. If you want the audience to ask questions during or after the presentation, say so.

“There will be a Q&A session after the presentation” “Please feel free to interrupt me if you have any questions” “I will be happy to answer your questions at any time during the presentation”

6. Make a Clear Transition in Between the Parts of the Presentation

Using transition words and phrases in English makes your presentation look smooth and easy to follow.

“I’d like to move on to another part of the presentation…” “Now I’d like to look at…” “For instance…” “In addition…” “Moreover…” “This leads me to the next point…”

7. Wow Your Audience

If you are not excited by your presentation, your audience will not be excited either. When presenting, you should plan to wow your audience. Use adjectives and descriptive words as they will help to attract the audience’s attention and make your speech more vivid and memorable.

“The product I present is extraordinary.” “It’s a really cool device” “This video is awesome” “This is an outstanding example”

8. Make Your Data Meaningful

If you need to present numbers or some comparative analysis of algorithms for integration, use some visuals to present it. You can use charts, graphs or diagrams to make your data meaningful and visually attractive. Remember that pie charts are good for representing proportions, line charts to represent trends, column and bar charts for ranking.

“Here are some facts and figures” “The pie chart is divided into several parts” “The numbers here have increased or gone up” “The numbers change and go down (decrease)” “The numbers have remained stable”

9. Summarize

At the end of the presentation, briefly summarize the main points and ideas. Provide the audience with your opinion and give them a call to action, let them know what you want them to do with the information you’ve shared. End of the presentation by thanking all the listeners and inviting them to the Q&A.

“Let’s summarize briefly what we’ve looked at…” “In conclusion…” “I’d like to recap…” “I’d like to sum up the main points…”

10. Practice

Try rehearsing your presentation using the above tips. Practice in front of a mirror or with your friends, parents or spouse. The more you practice, the better. While practicing, try not to use crutch words (examples: uhhhhh, ahhhh, so on, you know, like etc.)

Good luck with your presentation!

Enjoy this post? Please share!

Share on Facebook Share on Twitter Share on Linked In Share by Email

Privacy Overview

Effective Presentation Techniques – The Top 10

We have condensed all of the presentation techniques down to the most effective. Here are the Top 10 effective presentation techniques.

1. Use visual aids

Using pictures in your presentations instead of words can double the chances of meeting your objectives.

2. Keep it short and sweet

There is an old adage that said – “No one ever complained of a presentation being too short.” Nothing kills a presentation more than going on too long.

There are some college professors who will penalise a short presentation (most lecturers see no problem in droning on) , but for most people a shorter presentation is better. Keep your presentation to under 22 minutes if you can.

3. Use the rule of three

A simple technique is that people tend to only remember three things. Work out what the three messages that you want your audience to take away and structure your presentation around them. Use a maximum of three points on a slide.

4. Rehearse

Practice makes for perfect performance. Many experts say that rehearsal is the biggest single thing that you can do to improve your performance. Perform your presentation out loud at least four times. One of these should be in front of a real scary audience. Family, friends or colleagues. Even the dog is better than nothing.

5. Tell stories

All presentations are a type of theatre. Tell stories and anecdotes to help illustrate points. It all helps to make your presentation more effective and memorable.

6. Lose the bullet points – don’t put your speaker notes up on the screen

Bullet points are the kiss of death for most presentations. Most people use bullet points as a form of speaker notes. To make your presentation more effective put your speaker notes in your notes and not up on the screen.

7. Video yourself

Set up a video camera and video yourself presenting. You will see all sorts of mistakes that you are making, from how you are standing, if you are jangling keys, to how well your presentation is structured.

8 . Know what slide is coming next

You should always know when presenting which slide is coming up next. It sounds very powerful when you say “On the next slide [Click] you will see…”, rather than than a period of confusion when the next slide appears.

9. Have a back-up plan

Murphy’s law normally applies during a presentation. Technology not working, power cuts, projector blowing a bulb, spilling coffee on your front, not enough power leads, no loudspeakers, presentation displays strangely on the laptop – all of these are things that have happened in presentations that I have given.

Have a back-up plan. Take with you the following items – a printed out set of slides – (you can hold these up to the audience if you need to), a CD or data stick of your presentation, a laptop with your slides on it. Just in case it goes wrong.

Guess what? When you have back-ups – you seldom need to use them.

10. Check out the presentation room

Arrive early and check out the presentation room. If you can make sure that you see your slides loaded onto the PC and working on the screen. Work out where you will need to stand.

Do you agree or disagree with any of these effective presentation techniques? Have you have any experiences like this? Add it in to the comments box below.

Recommended Pages

thanxxx alott for the informationn they r very usful…

They are truly powerful which everyone should apply to make his/her presentation a complete success.

Thank you! Really interesting and important material.

thank you for the top 10 effective presentation techniques

Simple yet very powerful

One thing to add to point 6 Indeed, speaker notes should not be on the slides. Nothing is more boring when sombebody reads exactly what is on the slides, I’d better take a copy home and read it in quietness then.

well….i thought i wouldn’t be lucky but im just da luckiest person in the world who know these different presentation techniques…. but well done i will use these tips while preparing my presentation for accounting… thank you … Nice day…

thts really an amazing to have these presentation techniques.i’ll do my best to follow it while delivering my presentation.

i shall teach these techniques to my students when insha Allah i will be an instructor of spoken English.

Great! Anything on stage fright?

A speaker should keep an eye contact with all the people in the room while giving the presentation .

Rest the tips are useful .Thank u

i think all the technique are excellent

Its really helpful.

Thanks & Regards Shiva.

this is corny

very interesting for me, when you prepare a presentation

According to me you have missed the most vital thing “Know your audience”

Nothing has been said about the element of interaction. It’s clear that a presentation is being made, but, if the audience is engaged, there might be greater attention to the entire presentation.

This is just my take, views may vary.

I am a facilitator in community forestry.these points are powerful materials. However I would like if you can explain more about the number 6. What to use instead of bullets. I have in my mind that slides are the guide of my presentation so I have to use bullets?. On the other side, could you please send me a short presentation prepared with these techiniques and observe the application. at least, one slide I can to observe how is a slide well prepared.

Thanks a million from Colombia

Thank for this 10 points!

I have been training and I feel these are the 10 most important points as well

I find these techniques quite useful, I have to do a presentation on Vending Machines to my head teacher – and you made very strong and strategic points. I’m only in Year 7…

This is highly informative and without doubt, very effective

very good and effective…use this techniques to have a successful presention

I was just making a presentation & I have come to know that my presentation is simply boring & killing. Any way, very effective & informative points.

Life changing, thank you.

I am going to be facilitating a parenting course in a few weeks and loved the idea of of the rule of three to present my message.

tanks fot the info is so important to my life

thankx 2 you for providing me such an informative material. . .

but u forget to mention about dressing of a presenter and can u plzzzzzzzzzzz send me a slide which is one of d perfect one’s. . .

thanks alot……… you khnow i will try to do all these tips in my presentations….

[…] a site which has the top ten effective presentation techniques and they make sense to […]

Like mpz I also think there should be a section/point on knowing your audience.

Roughly (and shortly) speaking there are three styles of learning that each might influence an otherwise excellent presentation: Visual, auditory and sensitive.

The visual learners prefer imagery (Seeing is believing) and requires few words to every slide. Use images, diagrams, tables and such.

The auditory prefers verbal explanations and responses. Encourage questions during the presentation and be prepared to go outside the presentation if it is appropriate. Watch your tone, pitch and volume of voice. Don’t drone 😉

The sensitive learners needs to be connected to you. Use brief statements and demonstrations immediately followed by Q&A. Don’t focus on logic and external elements. Share personal values and experiences. Show empathy and understanding.

Just a short remark 😉

Thanks a lot. Its really very helpful for update and improving my life.

these are realy good tips for presentation.i think there should be some more easy tips which can make our presentation more effective.

It is really nice and helpful

Thank you, it was really helpful, I used to put bullets in my slides, now not anymore, thanks again!

thank u.. that’s really powerful

Guess this is really useful..as we say nothing is perfect but this can go to a great extent forming base, helping individual to build further on these lines!!

i hope my presentation would go well

Thanks a lot, really helpful!

Very good points the 10 ones; also Know the subject, know your audience, be confident when you present your concise presentation which might be effective if you add spice to it (related stories / jockes…) and wake up calls (sudden questions at randomly picked up person from the audience), and for better memorisation, make your objectives clear at beggining and summarise the essential points at the end(using primacy and recency effects at work)… I mostly liked the Murphy’s law, the worst sure happens to the one who does not have a back up plan. Thanks a million… From Ethiopia

Brilliant trigger points. How can I overcome shyness in students who have the Knowledge but can’t present? It is so frustrating.

thanks to you, i won my pitch for the new coca cola commercials they are releasing over here in the states! i make that about $4.5 million U.S i owe you for these tips:)!

Congratulations for your tips on effective teaching presentation! However , how can a teacher in a remote area of Burundi or Malawi get access to some of the materials you have earlier mentioned such as CD, Laptop,… Fine ! May you please suggest what may replace those HITechs that are not available to most of Third World School? May God bless you! Nayingunge from Burundi.

thank you, i believe that with practice i will get better.

thanks to providing perfect informatiom about presentation techniques ,they are really so usefull while preparing any kind of ppt or presentation,its everything

Experience… Great

Very nice Techniq Great Jobs

very well instructions

thanks ..tomorrow is my presentation I’ll apply all the points.IT REALLY BOOST ME UP!!!!!! thanks again

good presentation advice

AWESOME ADVICE & IT REALY WORKS

thank you, i believe that with practice i will get best of the best.

thanks for the information, now i know how to make a good presentation ..

THANK YOU VERY MUCH FOR SHARING YOUR KNOWLEDGE!!!GODBLESS YOU AND YOUR LOVE ONES:)

thank you for the information ,its really helpful.

wow they r really helpfulx

thank you from Saudi Arabia

very awesome that is

thanks it was very useful to me

yes….. very nice because i fully unaware about these techniques …. bye the way i am MBA student ….therefor it is very usefull for me….

Great advice. Thanks

Thanks… Good Tips.

Its was great list of advice about presentation. Thanks.

It’s really useful to have these 10 points when doing presentations. I’m a teacher and this will help me to present things well.

Thanks a lot

Regards Nimal

this has been really helpful 4 me i mean this step is very good it help me out at my presentation and i got all mos 90% on my presentation. i think more people should take time reading this 10 tip

THNKS MUCH 4 BRIEF SUMMARY ON PRESENTATION TECHNIQUE,MAY U INCLUDE ATLEAST DRESSING CODE

thanks for the info regarding presentation techniques,,,it help me out for my presentation some day.

thank u alot realy it is an important material!

Thank yo verry much for all the4 informtions which i enjoyed-am practicing..However at one point where you state that “Keep your presentation to under 22 minutes if you can.” As a technical trainer in my organisation(a tire industry in India)where I have a 5 day sessions (9.00-5.30 p.m)this 22 mts. concept is hard to follow. But inadvertently I don’t dwell on a single topic/concept more than 20 mts, Is it O.K. Thangarajan.P.K.

its really nice for understanding

nice presentation skills

This is just brilliant

This is good stuff. I was a trainer in Zimbabwe so to the gentleman from Burundi I would say that you don’t need fancy aids to make an effective presentation. Pre-prepare a series of flip chart pages with your main points on and use a separate blank flip chart for points made by your audience. Also on visual aids I find that so often every slide looks the same – same font, background, company logo in the corner and so on. For the bits you want them to remember, change the slide completely so it stands out.

gostei muito das técnicas

I LIKE THE THECNIQUES,THANK YOU

Nice techniques……..

thanksfor thes points

This was very helpful… not only for our Philosophy class, but for all college courses. All 10 recommendations were very good. However, the 2 that seemed the most useful of all were to (1) video record yourself to find out how you look… and (2) have a back-up plan ready.

Hey, Hatts off to you man, they are very useful for a layman going for his / her first presentation.

wonderfull stuff!!!

these tips maked me to know more about presentation

tanks .it is very useful in my life

Thanks for the advice… 🙂

this website is amazing thanks so much xx

Ya , friend ….. My Father also likes Powrpoint preaentations & doing commentary …… He & I both likes this two tasks ….. & he is expert explaining ppt presentation in public .. I too wanted to become like him & the tips u had given r the same as what my father always follows ……… So , Thanks

its good 4 me

thank you very much this was very helpful

Thanks a lot for wonderful ideas. I do hope it will be very helpful in my upcoming presentation. May God bless you!

I’ll try to do this for my report on Monday. Thank you.

When using beamer or slides please also look from audience side! As the outside sun might blind them.

dont be over confident be confident

Highly appreciated your tips on business presentation.they will be of my great help in my agribusiness forum next week. Regards

rely great!

Really useful tips, looking forward to have these kinds of tips in future.

Superb info… Tqz

very helpful and valuable points

Very useful info….

these are very informative tips.any perhaps very effective ones

Thanks , very useful

tell stories really helped

The rule of three is something which Id like to try. I would do presentations using bullets as keys — just learned that it’s not advisable to do it.

Thank you very much it has greatly helped.Blessed all the content is useful and with this i hope to get better

Wonderful, l suggest you need to talk like a thought leader as well.

I’m so grateful for this opportunity of visiting this site. I find them so interesting, all the points outlined in this writing. I so much like the self-videoing part of it. This gives you the clear picture of how bad or good your presentation style is. And also gives you the chance to know if your recent pattern is better than the former or not.

From Nigeria

All the points are valid, but particularly like point # 5 which talks about stories. Stories bring life and authenticity to your presentation. Great job!

• All Templates
• Persuasive Speech Topics
• Informative
• Architecture
• Celebration
• Educational
• Engineering
• Food and Drink
• Subtle Waves Template
• Business world map
• Filmstrip with Countdown
• Blue Bubbles
• Corporate 2
• Vector flowers template
• Editable PowerPoint newspapers
• Hands Template
• Red blood cells slide
• Circles Template on white
• Maps of America
• Light Streaks Business Template
• Zen stones template
• Heartbeat Template
• Web icons template

Presentation

8 Types of Presentation with Examples and Tips

Table of Contents

Every presentation is different, reflecting your unique business and the information you share. But, some common presentation types are used across various fields and teams. Before diving into specific slides or organization, consider the type that best suits your audience.

Here are some questions to get you started: Is your goal to inform or entertain? Who will you be speaking to: colleagues, investors, or potential customers? By thinking about these questions, you can choose the presentation format that best supports your message.

SlidesAI can help you simplify this process even further by providing descriptions of different presentation types.

Why Do We Need Different Types of Presentations?

Presentations are a great way to share ideas and information in different situations, depending on who you’re talking to. What you want to achieve with your presentation can change who it’s for and how you present it. For instance, if you’re trying to sell something, you might want a presentation that convinces people and is visually interesting. On the other hand, teaching something might require a more step-by-step approach with lots of details.

The best type of presentation depends on a few things, like what you’re trying to accomplish, the audience’s interests, and what you’re good at as a presenter. By choosing the right kind of presentation, you can get your message across clearly and achieve what you set out to do.

What are Different Types of Presentations?

1. educational presentations.

Educational presentations are a great way to introduce a new topic to people who aren’t familiar with it. They can be especially helpful when you want to explain something complex, like a process, or share important facts in a clear way. Whether you’re a teacher in a classroom or a trainer at a company, educational presentations can be a powerful tool for learning.

These presentations often use visuals like pictures or diagrams to make things easier to understand. They might also include step-by-step instructions to guide the audience through a process. Companies use them a lot to teach new employees about how things work at the company. The length of the presentation can be short or long, depending on what you’re trying to teach.

2. Instructional Presentations

Instructional presentations help people learn more about a topic and sometimes even guide them on what to do next. They’re similar to presentations used for education, but they might include some extra details or specific steps for the audience to follow.

Think of webinars or training sessions – these are examples of instructional presentations. They give people new information and help them develop new skills. For instance, if you’re in HR, you might create one to explain how employees can sign up for the new insurance plan.

Checkout Our Business Presentation Templates Download Free Business Presentation Templates Now!

3. Persuasive Presentations

Many presentations aim to convince the audience of something, like a new idea, product, or way of doing things. They often address a specific issue and use facts and figures to explain why their solution is the best. Business proposals and sales talks are common examples.

For instance, a new company seeking funding might create a presentation to convince investors to support their idea. This presentation could explain a problem they see in the market, how their company solves it, and how they plan to make money. A similar presentation could also be used to secure additional funding for growth and future plans.

4. Motivational Presentation

Motivational presentations aim to lift up the audience’s spirits and help them deal with challenges. They spark interest in a subject and share a particular perspective or message. These presentations can be useful when you want to inspire a group of people. Sometimes, they might even use a personal story to connect with the topic.

Leaders in organizations often use motivational presentations to boost employee morale and encourage them to work harder. Recruiters might also use them to showcase employee success stories and get potential hires excited about joining the company.

5. Problem-solution Presentation

Have you ever needed to present an idea to help people make a decision? Problem-solution presentations are a great way to do that. They focus on explaining a challenge or issue and then offering potential solutions for the audience to consider. While similar to persuasive presentations, the main goal here is to discuss the problem clearly and share research so decision-makers can weigh the options and choose the best path forward. These presentations can include details about the problem and a few possible solutions. They’re a handy tool for many business meetings and discussions within organizations.

6. Project Presentations

Progress presentations are a way to share how a project, campaign, or initiative is moving along. They’re similar to progress reports, but in a presentation format.

These presentations typically cover a few key points:

• Important measurements : This could include numbers or data that show how the project is doing.
• Current status : An update on where things stand at the moment.
• Potential roadblocks : Any challenges that might come up down the line.
• Tasks still to do : What needs to be completed next.

Project teams often use progress presentations to share updates on their work. This allows clients, colleagues, or other interested parties to stay informed and ask questions if needed.

7. Storytelling Presentations

Presentations that use a story format can be a great way to connect with your audience and share information in a more engaging way. This approach can be useful in many settings, from classrooms to company meetings. It can be especially helpful when you want to grab the attention of a specific group of people and make them feel involved.

Storytelling presentations might include personal stories or examples that relate directly to the main topic. For instance, if you’re in marketing, you could use a story format to present a case study to your colleagues about a competitor’s product and its success.

Checkout Our Templates for Your Product Marketing Download Marketing Presentation Templates Now!

8. Visual Presentations

Presentations come in many forms, but some rely mostly on pictures, charts, and other visuals instead of text. These are called visual presentations. They’re a good choice when you have limited time or your topic is easy to understand with pictures.

The goal of a visual presentation is to help people grasp the information quickly and keep them engaged. Businesses often use them to show what their products or services can do. For instance, a company selling shampoo might use before-and-after pictures to show the results.

Tips for Delivering an Effective Presentation

• Taking Notes: To help remember what to say during your presentation, jot down some brief notes. Keep them simple and focused on keywords or short directions. This will allow you to connect with your audience and avoid missing any important points.
• Knowing Your Audience: A little research about your audience before your presentation goes a long way. Understanding who they are and what they might be interested in helps you tailor your presentation to better address their needs and expectations.
• Planning for Interaction: Think about how much audience interaction you want based on the length, purpose, and type of information in your presentation. This may involve allocating more time for questions and discussion.
• Know yourself: Think about how comfortable you feel speaking in front of a group, especially if you don’t know everyone. Consider your strengths and weaknesses as a presenter and how you can play to your strengths and improve on your weaknesses.
• Practice Makes Perfect: Practicing your presentation beforehand, regardless of your experience level, can boost your confidence and help you identify areas for improvement. Go through each slide while talking to solidify the flow. Recording yourself can also be helpful.
• Be Prepared: Technical problems can happen, so having a plan can help you avoid delays. If it’s an in-person presentation, arriving early allows you to check the venue and ensure the equipment works properly.

How Does Slides AI Help with Presentations?

As you’ve explored, presentations come in various forms, each serving a distinct purpose and requiring a tailored approach. But regardless of the type, creating an impactful presentation can be time-consuming. This is where Slides AI steps in to streamline the process.

By leveraging SlidesAI’s functionalities – from generating outlines and suggesting designs to offering content recommendations – you can significantly reduce the time and effort invested in crafting your presentation. This frees you to focus on the finer details, like refining your message and practicing your delivery.

A well-organized and visually appealing presentation can really grab your audience’s attention and help them understand your message better. SlidesAI can help you achieve that, turning you from someone who just puts slides together into someone who can communicate confidently and leave a lasting impression.

Create presentation slides with AI in Seconds in Google Slides

10M+ Installs

Works with Google Slides

Frequently Asked Questions

How can i grab attention at the beginning of my presentation.

There are several ways to hook your audience from the start. Try opening with a surprising fact, a thought-provoking question, or even a short, interesting story related to your topic.

How long should my presentation be?

Ideally, aim for a presentation between 10-20 minutes. This timeframe allows you to cover the important points without losing your audience’s attention.

What are the 5 keys to a successful presentation?

Here are 5 keys to delivering a pitch-perfect presentation:

• Know your audience
• Master your material
• Make it a conversation
• Be adaptable
• Show empathy

Which presentation software should I use?

Several popular options are available, including Microsoft PowerPoint, and Google Slides . The best choice depends on your specific needs and comfort level. Additionally, SlidesAI.io is a helpful tool for creating visually engaging presentations. Consider your needs and choose the software that best suits you.

Related Posts

Create Effective Presentation Outlines: A Step-by-Step Guide with Tips & Examples

A presentation outline is like a roadmap for organizing your thoughts and delivering your message smoothly during a presentation. It helps you structure your content logically, ensuring that your audience can follow along easily. By providing a clear framework, an outline enhances the clarity and effectiveness of your presentation.

How to Loop a PowerPoint Presentation?

PowerPoint presentations are a go-to for clear and informative content delivery. But what if you want your presentation to run on repeat, like at a kiosk or digital sign? The good news is, that PowerPoint has a built-in feature to loop your slideshow, ensuring your message stays on display without interruption.

How Many Slides Do You Need for a 10-Minute Presentation?

Learn the ideal number of slides you need for a 10 minute presentation, including tips on content and staying on time.

Save Time and Effortlessly Create Presentations with SlidesAI

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

Do You Have What It Takes to Give a Great Presentation?

• Michael Foley

Three skills anyone can learn.

Great presentations are all about how well you engage your audience. Here are three ways to do that:

• Be balanced: Strike the right balance between structure and improvisation during your presentation. Rather than preparing your content in a narrative form, take the time to segment it by topic. Leave room to respond to your audience’s immediate needs, even if that means going off script for a while.
• Be generous: You goal should be to offer your audience something of value. Let this  principle guide the content you choose to present.
• Be human: Rehearse to familiarize yourself with your content, but do not memorize it. If you go blank for a moment, don’t apologize and act flustered, just pause, take a breath, collect your thoughts and continue on. Your audience wants you to be relatable.

Where your work meets your life. See more from Ascend here .

Have you ever seen a really great presentation? Honestly, they’re pretty rare.

• Michael Foley is an educator and coach, and founder of Clarity Centra l, a communications training and consulting firm based in Chicago. He is also an adjunct lecturer of leadership at the Kellogg Graduate School of Management at Northwestern University.

Partner Center

More From Forbes

How to make your presentation sound more like a conversation.

• Share to Facebook
• Share to Twitter
• Share to Linkedin

The main difference between strong, confident speakers and speakers who seem nervous in front of the room is in how relaxed and conversational they appear. Here are some basic pointers that will help you create a conversational tone when speaking, regardless of the size of your audience.

1. Avoid using the word, “presentation.” Every time you say, “I’m here to give you a presentation on X,” or, “In this presentation, you’ll see…,” you are emphasizing the formal, structured, sometimes artificial nature of the interaction. No one wants to be “presented” to. Instead, use language that emphasizes a natural, conversational exchange. “We’re here today to talk about X,” or “Today I’ll be sharing some ideas regarding Y.” You can even go so far as to say, “I’m glad we have time together today to discuss Z.” Even if your talk is not going to truly be a dialogue, you can use language that suggests engagement with the audience.

2. If you are using PowerPoint, avoid using the word “slide.” Instead of talking about the medium, talk about the concepts. Swap out, “This slide shows you…,” for, “Here we see….” Instead of saying, “On that slide I showed you a moment ago,” say, “A moment ago we were discussing X. Here’s how that issue will impact Y and Z.” Casual conversations don’t usually involve slide decks. Just because your complicated presentation on tax exposure, supply chain issues, or new health care regulations requires you to use slides, doesn’t mean you have to draw attention to that fact that the setting is formal and structured.

3. For many large-group events, speakers are provided with what’s called a “confidence monitor,” a computer screen that sits on the floor at the speaker’s feet showing the slide that appears on the large screen above the speaker’s head. Avoid using confidence monitors. Our natural inclination when using a confidence monitor is to gesture at the bullet point we’re discussing at the moment. However, we are pointing to a bullet point on the screen at our feet, which the audience can’t see, so it creates a disconnect between us and the audience. Instead, stand to the side of the large screen and gesture at the bullet point you’re talking about so that the audience knows which point you are discussing at the moment.

4. Don’t tell your audience, “I want this to be interactive.” It’s your job to make it interactive. If you are delivering the type of presentation where your audience size allows you to create true engagement with your listeners, create that connecting in stages to “warm up” the audience. Stage One engagement is to ask the audience a question relevant to your topic that you know most of the audience members can respond to affirmatively. “Who here has ever bought a new car?” or, “How many of you have ever waited more than 5 minutes on hold on a customer service line?” Raise your hand as you ask the question to indicate to the audience how to respond. Whoever has raised their hand has now participated in the discussion. They have indicated a willingness to engage. Stage Two engagement is calling on one of the people who raised their hand and asking a specific, perfunctory question. Again, it needs to be a question they can answer easily. If your first questions is, “Who here has bought a new car?” you can then call on someone and ask, “How long ago,” or “What kind of car did you buy most recently?” If your first question was, “Have you ever waited on hold for more than 5 minutes,” you can’t ask, “What company were you calling at the time?” The people who raised their hands weren’t thinking of a specific instance; they were just thinking broadly about that type of experience. You could, however, call on someone and ask, “Do you prefer when they play music or ads for the company’s products?” Anyone can answer that question. At that point, you are in an actual dialogue with that person. Stage Three engagement is asking them a question where they need to reveal something more personal. “How does that make you feel when you hear those ads?” You’ve warmed up your audience and drawn them in with baby steps. Now you have actual, meaningful audience participation.

Best High-Yield Savings Accounts Of 2024

Best 5% interest savings accounts of 2024.

5. Use gestures. When we’re speaking in an informal setting, we all use hand gestures; some people use more than others, but we all use them. When we try to rein in our gestures, two things happen that diminish our speaking style. First, we look stiff and unnatural. We look like we are presenting a guarded or cautious version of ourselves; we look less genuine. Second, hand gestures burn up the nervous energy we all have when speaking in front of a large group. That’s good. When we try to minimize our hand gestures, we tie up that nervous energy and it starts to leak out on odd ways, where we start to tap our foot, fidget with our notes or microphone, or tilt our head side to side to emphasize key points. Just let the gestures fly. It’s unlikely they will be too large or distracting. I have coached people on their presentation skills for 26 years. In that time, I have met three people who gestured too much. Everyone else would benefit from using their gestures more freely.

The impact we have as communicators is based on the cumulative effect of many different elements of our delivery. These suggestions alone won’t make you a terrific presenter. They will, however, add to the overall package your present of yourself when speaking to large audiences.

• Editorial Standards
• Reprints & Permissions

Join The Conversation

One Community. Many Voices. Create a free account to share your thoughts. 

Forbes Community Guidelines

Our community is about connecting people through open and thoughtful conversations. We want our readers to share their views and exchange ideas and facts in a safe space.

In order to do so, please follow the posting rules in our site's  Terms of Service.   We've summarized some of those key rules below. Simply put, keep it civil.

Your post will be rejected if we notice that it seems to contain:

• False or intentionally out-of-context or misleading information
• Insults, profanity, incoherent, obscene or inflammatory language or threats of any kind
• Attacks on the identity of other commenters or the article's author
• Content that otherwise violates our site's  terms.

User accounts will be blocked if we notice or believe that users are engaged in:

• Continuous attempts to re-post comments that have been previously moderated/rejected
• Racist, sexist, homophobic or other discriminatory comments
• Attempts or tactics that put the site security at risk
• Actions that otherwise violate our site's  terms.

So, how can you be a power user?

• Stay on topic and share your insights
• Feel free to be clear and thoughtful to get your point across
• ‘Like’ or ‘Dislike’ to show your point of view.
• Protect your community.
• Use the report tool to alert us when someone breaks the rules.

Thanks for reading our community guidelines. Please read the full list of posting rules found in our site's  Terms of Service.

• 0 Shopping Cart $ 0.00 -->

28 Great PowerPoint Presentation Tips

A comprehensive list of PowerPoint presentation tips and tricks.

Microsoft PowerPoint has been around since 1987 and is by far the most popular presentation tool on the market but many people still struggle to give effective presentations. PowerPoint is often blamed but often this is really a case of a poor workman blaming his tools.

Audience polling tools like our ParticiPoll system can add an extra dimension to presentations but what about all the other things that make for a great presentation?

Here is our list of tips and techniques to help you deliver a fantastic presentation. Let us know if you can think of any others we should add!

New:  We now have a handy tool where you can upload and “ Analyse My Presentation ” to get live feedback on you PowerPoint presentation file, just follow the link.

Creating Your Presentation

Follow the 10-20-30 rule.

Guy Kawasaki wrote that a presentation “should have ten slides, last no more than twenty minutes, and contain no font smaller than thirty points”. He was talking about pitching to investors but this is fairly solid advice for any presentation. You might need to over-run the 20 minute rule in some circumstances (e.g. a university lecture) but could the additional time be better used for questions and answers?

Start With A Summary

Summarising your presentation in a single slide at the beginning gives your audience a clear idea of what they’re going to learn and stimulates anticipation of the whole story. It’s also a good discipline for you as a presenter to help keep you keep the topic succinct. If you can’t summarise your presentation topic in 10-15 words, then it’s probably too long or too vague. Think of is an ‘elevator pitch’, a synopsis of a book or an abstract for a scientific paper.

Tell A Story

Human beings have used stories to impart information since the dawn of time and it’s still a great way to communicate. Even if you have to deliver a long series of facts, remember that it’s the underlying meaning or outcome of those facts that will strike home.  This doesn’t mean you should start your presentation with “Once upon a time”, just that you should build it in such a way that the chronology of the topic is clear.  Can you think of plot twists or hooks that can be shared along the way to keep them interested? You might find writing an initial ‘script’ away from PowerPoint helpful before you go diving into slides.

See It From The Audience’s Perspective

Getting the tone and content of your presentation right starts with being honest about what they really want to hear and what they can realistically absorb. If you really care about your audience, you have to be an advocate for their learning needs not your own agenda. If that means simplifying your content or recapping previous presentations then so be it. It’s better than losing them completley or being “that presenter” who was too difficult to understand or didn’t recognise who he/she was speaking to.

Present What You Know And Care About

Most lower-quality presentations are a symptom of the presenter not really wanting to be there. A rookie presenter who knows their subject or is really passionate can be better than a pro who isn’t bothered. Just look at Elon Musk – his presentation style is notoriously haphazard but he is incredibly exciting and comes across as completely authentic. The very best presenters know their subject so well that they don’t even need notes or slides. If you don’t know or don’t care then don’t present – find someone else!

Avoid Too Much Text

Using too much text is one of the most common presenting mistakes. Presenters often feel they need to include everything in their slides. This often manifests itself in over-use of bullet point lists, paragraphs of text and tiny font sizes. A couple of sentences per slide and no more is the ideal and remember that the audience came to hear you speak not read. A good test on the day is to see whether they audience are mostly looking at you or the slides – if its the latter then you’ve put too much content in!

A picture tells a thousand words and good images are far better than tons of text. Don’t use cheesy stock imagery though – that’s a real turn off. Choose pictures that directly illustrate or support what you’re saying or set the tone of the slide. In the right setting, a bit of humour can cheer the audience up and keep them engaged too (there are loads of great Internet meme graphics you can use or adapt.) Videos can work well too but its best to keep to shorter snippet videos rather than diverting half your presentation slot to something pre-recorded.

Customise Your Template

Far too many presenters stick to the standard blank PowerPoint template. PowerPoint comes with lots of other template and font choices to improve appearance.  It’s also really easy to create your own custom PowerPoint templace with your own logo, font, etc.

Don’t Over-Use Animations

Subtle slide-ins or fade-ins of the next slide can add a bit of style to a presentation but sliding-in every last bulletpoint becomes irritating on a longer presentation. Keep it simple!

Present Data Clearly

It can be tempting to chuck in a spreadsheet of raw data and try to explain it figure-by-figure but a chart or graph will highlight the significance of your data far better. Be sure to pick the right sort of chart for your data. Typically you would use a histogram to compare quantities, a pie chart for percentages and a line chart to show change over time.

Use the Slide Sorter

Inspirational ideas for slide content don’t always come out in a sensible order for the presentation itself. Once you’ve written your main slides use the slide sorter (View Menu > Slide Sorter) to put the slides in an order that fits the overall story of your presentation. Audience retention is improved by having sub-topic chunks within your presentation so try to bring slides together in mini-segments.

Avoid Death By PowerPoint

Death by PowerPoint is a phrase used to describe a multitude of sins. In almost every case it’s the presenter who is at fault not PowerPoint. The most common cause is making the slide deck the focus rather than the presenter. If you don’t want to be there and could just as easily email your slides to your audience, then do that and spare everyone.

Preparation For The Event

You’ve probably put hours or even days into getting your presentation content right so don’t spoil it by not preparing on the day. Ideally you should run through your slides in the same room and on the same device that you will be using on the day. This will avoid local technical issues (e.g. lack of Internet connection, poor slide projection, lack of sound, wrong presentation software, etc.) Be sure to turn off your screen saver too! There are many technical facing comes when we deal with technology. To get knowledge about resolve these technical issues fastly and effectively click here .

Practicing in front of a mirror isn’t the same as doing it in front of an audience and it might make you more self-conscious. Start your presentation training with small, friendly audiences and speak about something you’re totally familiar with. Then you can work your way up to larger audiences and more tricky topics.

Coping With Nerves

Imagine the audience naked! If you’re new to public speaking or are speaking to a new crowd, it can be pretty nerve-wracking. Turn this on its head be imagining the front row are all naked and desperately self-conscious!

Speak Slowly

It’s tempting to think that you need to divulge as much information as possible but talking too fast is really hard for audiences to digest. Watch a TV newscaster and see how the speak slowly with lots of pauses. It’s definitely a case of “less is more” and you’ll be amazed how much better the audience absorb stuff. The breathing space will also give you more brain ‘CPU time’ to gauge audience reactions and respond accordingly. Speaking too fast is a common trait of nervous speakers but ironically, slowing down will give you more time to relax and give your presentation more gravitas.

Keep To A Schedule

Presentations that over-run are hard work for the audience and a nightmare for event organisers. Keep an eye on the clock, try to avoid labouring points and don’t be afraid to skim less critical slides if you are running out of time. There’s nothing wrong with ending a little earlier than expected and it can give you an opportunity for an impromptu Q&A session.

If You Get Stuck

If you get stuck half way through a presentation or someone asks you a difficult question, don’t be afraid of taking a pause. It’s OK to buy time with “let me think about that” or “that’s a great question!”. At times like this it can help to go back to your presenation synopsis and use that to get you back on track.

Make Eye Contact

It’s very easy to end up staring at the one person on the front row who seem to be smiling at you but focussing on just one person or just staring into space makes the main audience feel like you’re not interested in them. With a small audience, be sure to move eye contact from person to person without fixating on any particular individual. If you have a larger audience, try scanning your attention from left-to-centre-to-right and back again focussing on random individuals each time. Don’t forget the people right at the back too!

Don’t Read From Your Slides

People don’t come to conferences or lectures to read stuff – they want to hear a human being (that’s you!) engage with them. It’s OK to use slide content as a cue occasionally but reading from the screen with your back to the audience is both lazy and boring to watch. If you need additional cues and are using a projector screen then use the Notes feature in PowerPoint – you can get the notes displayed only to you on your computer (Slides > User Presenter View) whilst the audience see only the main slide content on the screen.

Project Your Voice

It might sound obvious but you need to be heard! That doesn’t mean you need to shout, just that you should speak slowly using your lungs. Even if you have the benefit of amplification, you still need to make sure you’re speaking at a consistent volume near to the mic. With an informal audience, you can do your own little sound-check by asking if the people at the back can hear you.

Correct Microphone Use

Most handheld or podium mics need to be held a few centimetres away from your mouth. Speak across the top of the mic rather than directly into it otherwise you’ll hear loud thumps whenever you speak percussive syllables. Clip-on Lavalier mics that you attach to your lapel or collar can help you speak more naturally but try not to turn your head too much as you may end up speaking too far away from the mic. In all cases, speak with your normal voice (unless you’re a singer or performer!) and don’t drop the mic unless you’ve really had the last word!

Use Your Hands And Body

Body language is big part of communication but you don’t have to be a trained orator to get it right (and many politicians and TV personalities use wildly unnatural and contrived gestures anyway). It’s a classic case of “be yourself” – do use your hands, gestures and facial expressions to accentuate what you’re saying but don’t do anything that feels unnatural. If you’re a relatively reserved, non-animated person that’s OK – maybe you’re better at verbal wit or pithy comments? If you’re not into waving your hands then try gripping the outer edges of the lectern or walking around the stage as an alternative. If you’re worried about it then get a friend or colleague to sit in the audience and give you feedback after a presentation.

Ask Great Questions

Asking Socratic questions is a great way of engaging audience members brains and get them thinking ahead. They can often make great slide headings too. If your presentation schedule and environment allows, putting these questions directly to the audience can really liven up the talk. Try asking interesting questions that the whole audience can answer together using a show of hands or shout-outs. If it’s a sensitive subject then try using an anonymous feedback tool like ParticiPoll .

Avoid Classroom Chicken

Don’t ask the audience questions they don’t want to answer. “Is everyone having fun?”, “Who has done their homework?” or “would anyone like to put their hand up and tell me X?” will most likely be replied with whispered “Nos” or deathly silence. Disingaged audiences can often play a game of chicken with you or a game with Pro-Skins boosts, holding out on responses until the very last moment (or not at all!).

Hold A Q&A

If time permits, giving your audience an opportunity to ask questions either at the end or during the presentation is always a good idea. You often end up finding out what they really wanted to hear from you and this can be fed back into any future repeat of the presentation.

Share Your Slides

Sharing your slides with your audience after the presentation is a great way to help them recall the content of your presentation. It’s also a great way to encourage engagement after the event so don’t forget to include the date, time and title of the presentation as well as your contact details.

At the beginning of the presentation, be sure to tell them that you’ll be making the slides available so they don’t feel the need to spend too much time taking notes instead of watching you. Don’t share your slides or hand-out printed copies of your slides before the presentation otherwise you’ll spoil the show and give people an excuse to leave without watching.

Interact With The Audience

To “lecture” has become a dirty word implying presenting in a reprimanding or condescending manner. It also implies a one-way street whereas audiences love to give feedback, ask questions and steer the presention to suit their needs.

A traditional ‘show of hands’ can work but it tends to favour the know-it-alls and attention-seekers and allows audience members’ groupthink to sway the responses. Its also innappropriate for sensitive subjects where the audience may not feel confortable expressing themselves.

Polling and feedback systems like ParticiPoll  ( try it now for free!) are a great way of adding interaction into your existing presentations without too much setup hassle. They’re a great way to grab the audience’s attention (especially if they’re fiddling with their phones) and help you find out what they think.

These are the great ways to represent your presentation effectively. With these tips  you make a experts of handling presentation. Are you a presentation specialist? Find your job on Jooble .

Downloading ParticiPoll

Your file is downloading. Select ‘Save As’ if prompted

Can't download? Try a zipped copy

Download ParticiPoll

Click the button below to download the add-in, then mount the Participoll.dmg and follow the step by step instructions.

Don't double click!

Click the button below to download the add-in, then save it somewhere safe where it won’t get moved or deleted, then follow the step by step instructions.

Quantity Required

Select the pack size you required

Welcome back to ParticiPoll

Sign in below and start polling today!

Create Your Account

(free trial and purchase options available)

Thanks for registering!

You will be redirected to the plans page in 5 seconds or you can click here .

Microsoft 365 Life Hacks > Presentations > How to introduce yourself in a presentation

How to introduce yourself in a presentation

A well-executed presentation should captivate your audience and listeners. The first step to gaining their attention is creating an engaging introduction. Learn why presentation introductions are important and how to properly execute one for your presentation.

Why are presentation introductions important?

Presentation delivery impacts your audience’s reception and listening skills. A dull delivery can deter listeners and potentially leave them disinterested. Conversely, an effective delivery can engage your audience, promote active listening, and stimulate substantive discussion.

Presentation introductions also help to establish the outline of your presentation and give the audience an idea of what is to come. Introductions play a crucial role in captivating listeners from the onset and building momentum. They address who you are, why the audience should be invested, state the topic, establish credibility, preview the main points, and establish the cadence and tone of your presentation. Before you dive into the content of your presentation, ensure you establish an effective introduction to captivate your audience.

Tell your story with captivating presentations

Powerpoint empowers you to develop well-designed content across all your devices

How to begin a presentation introduction

To establish rapport with your audience, here are some tips to effectively introduce yourself and your presentation:

Be clear and concise

A succinct introduction makes it easier for your audience to follow. Keep your introduction simple, short, and include only necessary information. State your name and topic clearly so your audience knows you from the beginning. Avoid unnecessary details or lengthy anecdotes in your introduction to keep things focused and to the point.

Provide pertinent background information

In addition to your name and topic, highlight anything else that is relevant. You can include your education, work background, qualifications, and other information. Most importantly, ensure the information you disclose is directly relevant to yourself and presentation.

Create a hook or attention getter

Once you’ve established your name and topic, create an engaging hook or attention getter. Your introduction can be funny, clever, or it can captivate your audience. Have fun creating an introduction, but be sure to align your tone and delivery to your audience.

Outline your presentation

Let your audience know what your will be discussing. Establish a roadmap of your presentation: outline your contents, topics, and main points in an easily digestible format. This makes it easier for your audience to follow your presentation and prepare for its contents.

Practice and refine

Once you’ve created a solid introduction, rehearse your introduction until the delivery is organic and smooth. Confidence is key for an optimal delivery. Speak clearly, practice eye contact, and use storytelling to engage your audience.

Be authentic

Above all, be yourself—authenticity helps you build trust and connection with your audience. Carry you character, speech, and personality into your presentation to draw in your audience.

A successful introduction establishes tone, cadence, topic, and showcases your personality. Gain your audience’s attention and effectively deliver your presentation with an effective introduction. For more ways to engage your audience and improve presentation delivery , learn more presentation tips .

Get started with Microsoft 365

It’s the Office you know, plus the tools to help you work better together, so you can get more done—anytime, anywhere.

Topics in this article

More articles like this one.

How to add citations to your presentation

Conduct research and appropriately credit work for your presentation. Understand the importance of citing sources and how to add them to your presentation.

How to create an inspirational PowerPoint presentation

Boost your presentation skills by learning how to inspire and captivate your audience.

How to create an educational presentation

Use PowerPoint to create dynamic and engaging presentations that foster effective learning.

Five tips for choosing the right PowerPoint template

Choose an appropriate PowerPoint template to elevate your presentation’s storytelling. Consider time length, audience and other presentation elements when selecting a template.

Everything you need to achieve more in less time

Get powerful productivity and security apps with Microsoft 365

Explore Other Categories