This site is intended for health professionals only

- Newsletter sign up
- Nursing in Practice 365

The importance of a healthy diet and exercise

See how our symptom tool can help you make better sense of patient presentations Click here to search a symptom

Receive the latest news, clinical updates and case studies straight to your inbox.
SIGN UP TODAY
Related articles
Obesity levels remain worryingly high, with nearly 30% of the global population being overweight or obese. This figure is set to rise to almost half of the world’s adult population by 2030, according to the McKinsey Global Institute
Most Popular
1 Quick quiz: Test your knowledge of eczema
2 Practice nurses to vaccinate against RSV in new NHS programme
3 Long-awaited joint asthma guidance overhauls diagnostics and treatment
4 Safeguarding young people against gaming and gambling harms

Sign up for news alerts Subscribe to Nursing in Practice newsletters to ensure you receive the news as it happens in your inbox.
Join the discussion and be a part of Nursing in Practice
Sharpen your skills and further your career with Nursing in Practice
- Nursing in Practice Reference
Other links
- Contact Us
- Terms and conditions
- Privacy Policy
- Yellow Card reporting
Get the Nursing in Practice free app
Get our free diagnosis symptom tool
Other Cogora brands
- Pulse Today
- Hospital Healthcare Europe
- The Pharmacist
- Management In Practice
- Healthcare Leader
- Hospital Pharmacy Europe
© Cogora 2024 Cogora Limited. 1 Giltspur Street, London EC1A 9DD Registered in the United Kingdom. Reg. No. 2147432
Nursing in Practice newsletters
Sign up today to receive the latest news, business insight, blogs and case studies via newsletters as it happens.
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Cold Spring Harb Perspect Med
- v.8(7); 2018 Jul
Health Benefits of Exercise
Gregory n. ruegsegger.
1 Department of Biomedical Sciences, University of Missouri, Columbia, Missouri 65211
Frank W. Booth
2 Department of Medical Pharmacology and Physiology, University of Missouri, Columbia, Missouri 65211
3 Department of Nutrition and Exercise Physiology, University of Missouri, Columbia, Missouri 65211
4 Dalton Cardiovascular Research Center, University of Missouri, Columbia, Missouri 65211
Overwhelming evidence exists that lifelong exercise is associated with a longer health span, delaying the onset of 40 chronic conditions/diseases. What is beginning to be learned is the molecular mechanisms by which exercise sustains and improves quality of life. The current review begins with two short considerations. The first short presentation concerns the effects of endurance exercise training on cardiovascular fitness, and how it relates to improved health outcomes. The second short section contemplates emerging molecular connections from endurance training to mental health. Finally, approximately half of the remaining review concentrates on the relationships between type 2 diabetes, mitochondria, and endurance training. It is now clear that physical training is complex biology, invoking polygenic interactions within cells, tissues/organs, systems, with remarkable cross talk occurring among the former list.
The aim of this introduction is briefly to document facts that health benefits of physical activity predate its readers. In the 5th century BC, the ancient physician Hippocrates stated: “All parts of the body, if used in moderation and exercised in labors to which each is accustomed, become thereby healthy and well developed and age slowly; but if they are unused and left idle, they become liable to disease, defective in growth and age quickly.” However, by the 21st century, the belief in the value of exercise for health has faded so considerably, the lack of exercise now presents a major public health problem ( Fig. 1 ) ( Booth et al. 2012 ). Similarly, the lack of exercise was classified as an actual cause of chronic diseases and death ( Mokdad et al. 2004 ).

Simplistic overview of how physical activity can prevent the development of type 2 diabetes and one of its complications, cardiovascular disease. Physical inactivity is an actual cause of type 2 diabetes, cardiovascular disease, and tens of other chronic conditions ( Table 1 ) via interaction with other factors (e.g., age, diet, gender, and genetics) to increase disease risk factors. This leads to chronic disease, reduced quality of life, and premature death. However, physical activity can prevent and, in some cases, treat disease progression associated with physical inactivity and other genetic and environmental factors.
Published in 1953, Jeremy N. Morris and colleagues conducted the first rigorous epidemiological study investigating physical activity and chronic disease risk, in which coronary heart disease (CHD) rates were increased in physically inactive bus drivers versus active conductors ( Morris et al. 1953 ). Since this pioneering report, a plethora of evidence shows that physical inactivity is associated with the development of 40 chronic diseases ( Table 1 ), including major noncommunicable diseases such as type 2 diabetes (T2D) and CHD, and as premature mortality ( Booth et al. 2012 ).
Worsening of 40 conditions caused by the lack of physical activity with growth, maturation, and aging throughout life span
| 1. Accelerated biological aging/premature death |
| 2. Aerobic (cardiorespiratory) fitness (VO ) |
| 3. Arterial dyslipidemia |
| 4. Balance |
| 5. Bone fracture/falls |
| 6. Breast cancer |
| 7. Cognitive dysfunction |
| 8. Colon cancer |
| 9. Congestive heart failure |
| 10. Constipation |
| 11. Coronary (ischemic) heart disease |
| 12. Deep vein thrombosis |
| 13. Depression and anxiety |
| 14. Diverticulitis |
| 15. Endometrial cancer |
| 16. Endothelial dysfunction |
| 17. Erectile dysfunction |
| 18. Gallbladder diseases |
| 19. Gestational diabetes |
| 20. Hemostasis |
| 21. Hypertension |
| 22. Immunity |
| 23. Insulin resistance |
| 24. Large arteries lose more compliance with aging |
| 25. Metabolic syndrome |
| 26. Nonalcoholic fatty liver disease |
| 27. Obesity |
| 28. Osteoarthritis |
| 29. Osteoporosis |
| 30. Ovarian cancer |
| 31. Pain |
| 32. Peripheral artery disease |
| 33. Preeclampsia |
| 34. Polycystic ovary syndrome |
| 35. Prediabetes |
| 36. Rheumatoid arthritis |
| 37. Sarcopenia |
| 38. Stroke |
| 39. Tendons being less stiff |
| 40. Type 2 diabetes |
The breadth of the list implies that a single molecular target will not substitute for appropriate daily physical activity to prevent the loss of all listed items.
In this review, we highlight the far-reaching health benefits of physical activity. However, note that the studies cited here represent only a fraction of the >100,000 studies showing positive associations between the terms “exercise” and “health.” In addition, we discuss how exercise promotes complex integrative responses that lead to multisystem responses to exercise, an underappreciated area of medical research. Finally, we consider how strategies that “mimic” parts of exercise training compare with physical exercise for their potential to combat metabolic disease.
EXERCISE IMPROVES CARDIORESPIRATORY FITNESS
There is arguably no measure more important for health than cardiorespiratory fitness (CRF) (commonly measured by maximal oxygen uptake, VO 2max ) ( Blair et al. 1989 ). For example, Myers et al. (2002 ) showed that each 1 metabolic equivalent (1 MET) increase in exercise-test performance conferred a 12% improvement in survival, stating that “VO 2max is a more powerful predictor of mortality among men than other established risk factors for cardiovascular disease (CVD).” Low CRF is also well established as an independent risk factor of T2D ( Booth et al. 2002 ) and CVD morbidity and mortality ( Kodama et al. 2009 ; Gupta et al. 2011 ). Similarly, Kokkinos et al. (2010) reported that men who transitioned from having low to high CRF decreased their mortality risk by ∼50% over an 8-yr period, whereas men who transitioned from having high to low CRF increased their mortality risk by ∼50%.
Importantly then, from the above paragraph, physical activity and inactivity are major environmental modulators of CRF, increasing and decreasing it, respectively, often through independent pathways. Findings from rats selectively bred for high or low intrinsic aerobic capacity show that rats bred for high capacity, which are also more physically active, have 28%–42% increases in life span compared to low-capacity rats ( Koch et al. 2011 ). Endurance exercise is well recognized to improve CRF and cardiometabolic risk factors. Exercise improves numerous factors speculated to limit VO 2max including, but not restricted to, the capacity to transport oxygen (e.g., cardiac output), oxygen diffusion to working muscles (e.g., capillary density, membrane permeability, muscle myoglobin content), and adenosine triphosphate (ATP) generation (e.g., mitochondrial density, protein concentrations).
Data from the HERITAGE Family Study has provided some of the first knowledge of genes associated with VO 2max plasticity because of endurance-exercise training. Following 6 wk of cycling training at 70% of pretraining VO 2max , Timmons et al. (2010) performed messenger RNA (mRNA) expression microarray profiling to identify molecules potentially predicting VO 2max training responses, and then assessed these molecular predictors to determine whether DNA variants in these genes correlated with VO 2max training responses. This approach identified 29 mRNAs in skeletal muscle and 11 single-nucleotide polymorphisms (SNPs) that predicted ∼50% and ∼23%, respectively, of the variability in VO 2max plasticity following aerobic training ( Timmons et al. 2010 ). Intriguingly, pretraining levels of these mRNAs were greater in subjects that achieved greater increases in VO 2max following aerobic training, and of the 29 mRNAs, >90% were unchanged with aerobic training, suggesting that alternative exercise intervention paradigms or pharmacological strategies may be needed to improve VO 2max in individuals with a low responder profile for the identified predictor genes ( Timmons et al. 2010 ). Keller et al. (2011) found that, in response to endurance training, improvements in VO 2max were associated with effectively up-regulating proangiogenic gene networks and miRNAs influencing the transcription factor–directed networks for runt-related transcription factor 1 (RUNX1), paired box gene 3 (PAC3), and sex-determining region Y box 9 (SOX9). Collectively, these results led the investigators to speculate that improvements in skeletal muscle oxygen sensing and angiogenesis are primary determinates in training responses in VO 2max ( Keller et al. 2011 ).
Clinically important concepts have emerged from the pioneering HERITAGE Family Study. One new clinical concept is that a threshold dose–response relationship influences the percentage of subjects responding with an increase in VO 2max to endurance training volumes (with volume being defined here as the product of intensity × duration), as previously published ( Slentz et al. 2005 , 2007 ). Ross et al. (2015) later extended the aforementioned Slentz et al. studies. After a 24-wk-long endurance training study ( Ross et al. 2015 ), percentages of women and men identified as nonresponders to the training (i.e., defined as not increasing their VO 2peak ) progressively fell inversely to a two stepwise progressive increase in endurance-exercise training volume, as described next. Thirty-nine percent (15 of 39) of training subjects did not increase their VO 2peak in response to the low-amount, low-intensity training; 18% (9 of 51) had no increase in VO 2peak in the group having high-amount, low-intensity training; and 0% (0 of 31) who underwent high-amount, high-intensity training did not increase their VO 2peak . A biological basis for the dose–response relationship in the previous sentence could be made from an analysis of interval training (IT) and IT/continuous-training studies published from 1965 to 2012 ( Bacon et al. 2013 ). A second older concept is being reinvigorated; Bacon et al. (2013) indicate that different endurance-exercise intensities and durations are needed for different systems in the body. They suggest that very short periods of high-intensity endurance-type exercise may be needed to reach a threshold for peripheral metabolic adaptations, but that longer training durations at lower intensities are required to see large changes in maximal cardiac output and VO 2max .
A comparable example exists for resistance training. Maximal resistance loads require a minimum of 2 min/per wk for each muscle group recruited by a specific maneuver to obtain a strength training adaptation [(8 contractions/set × 2 sec/contraction × 3 sets/day) × 2 days/wk) = 96 sec]. As of 2016, one opinion from Sarzynski et al. (2016) for the molecular mechanisms by which endurance exercise drives VO 2max include, but are not limited to, calcium signaling, energy sensing and partitioning, mitochondrial biogenesis, angiogenesis, immune functions, and regulation of autophagy and apoptosis.
Perhaps more importantly, lifelong aerobic exercise training preserves VO 2max into old age. CRF generally increases until early adulthood, then declines the remainder of life in sedentary humans ( Astrand 1956 ). The age-related decline in VO 2max is not trivial, as Schneider (2013) reported a ∼40% decline in healthy males and females spanning from 20 to 70 yr of age. However, cross-sectional data show that with lifelong aerobic exercise training, trained individuals often have the same VO 2max as a sedentary individual four decades younger ( Booth et al. 2012 ). Myers et al. (2002) found that low estimated VO 2max increases mortality 4.5-fold compared to high estimated VO 2max . They concluded, “Exercise capacity is a more powerful predictor of mortality among men than other established risk factors for cardiovascular disease.” Given the strong association between CRF, chronic disease, and mortality, we feel identifying the molecular transducers that cause age-related reductions in CRF may have profound implications for improving health span and delaying the onset of chronic disease. In two of our recent papers, transcriptomics was performed on the triceps muscle ( Toedebusch et al. 2016 ) and on the cardiac left ventricle ( Ruegsegger et al. 2017 ). We were addressing the question of what molecule initiates the beginning of the lifelong decline in aerobic capacity with aging. Aerobic capacity (VO 2max ) involves, at a minimum, the next systems/tissues, as oxygen travels through the mouth, airways, pulmonary membrane, pulmonary circulation, left heart, aorta/arteries/capillaries, and sarcoplasm/myoglobin to mitochondria. We allowed female rats access, or no access, to running wheels from 5 to 27 wk of age. Surprisingly, voluntary running had no effect on the delay in the beginning of the lifetime decrease in VO 2max . Our skeletal muscle transcriptomics elicited no molecular targets, whereas gene networks suggestive of influencing maximal stroke volume were identified in the left ventricle transcriptomics ( Ruegsegger et al. 2017 ).
Publications concerning the effects of exercise on the brain (from 54 to 216 papers listed on PubMed from 2007 to 2016) have increased 400%. In addition, a 2016 study ( Schuch et al. 2016 ) of three previous papers reported that humans with low- and moderate-CRF had 76% and 23%, respectively, increased risk of developing depression compared to high CRF in three publications. With this forming trend, the next section will consider exercise and brain health.
EXERCISE IMPROVES MENTAL HEALTH
Many studies support physical activity as a noninvasive therapy for mental health improvements in cognition ( Beier et al. 2014 ; Bielak et al. 2014 ; Tian et al. 2014 ), depression ( Kratz et al. 2014 ; McKercher et al. 2014 ; Mura et al. 2014 ), anxiety ( Greenwood et al. 2012 ; Nishijima et al. 2013 ; Schoenfeld et al. 2013 ), neurodegenerative diseases (i.e., Alzheimer’s and Parkinson’s disease) ( Bjerring and Arendt-Nielsen 1990 ; Mattson 2014 ), and drug addiction ( Zlebnik et al. 2012 ; Lynch et al. 2013 ; Peterson et al. 2014 ). In 1999, van Praag et al. (1999) showed the survival of newborn cells in the adult mouse dentate gyrus, a hippocampal region important for spatial recognition, is enhanced by voluntary wheel running. Similarly, spatial pattern separation and neurogenesis in the dentate gyrus are strongly correlated in 3-mo-old mice following 10 wk of voluntary wheel running ( Creer et al. 2010 ), and the development of new neurons in the dentate gyrus is coupled with the formation of new blood vessels ( Pereira et al. 2007 ). Many exercise-related improvements in cognitive function have been associated with local and systemic expression of growth factors in the hippocampus, notably, brain-derived neurotrophic factor (BDNF) ( Neeper et al. 1995 ; Cotman and Berchtold 2002 ). BDNF promotes many developmental functions in the brain, including neuronal cell survival, differentiation, migration, dendritic arborization, and synaptic plasticity ( Park and Poo 2013 ). In rat hippocampus, regular exercise promotes a progressive increase in BDNF protein for up to at least 3 mo ( Berchtold et al. 2005 ). In an opposite manner, BDNF mRNA in the hippocampus is rapidly decreased by the cessation of wheel running, suggesting BDNF expression is tightly related to exercise volume ( Widenfalk et al. 1999 ).
Findings by Wrann et al. (2013) highlight one mechanism by which endurance exercise may up-regulate BDNF expression. To summarize, Wrann et al. (2013) noted that exercise increases the activity of the estrogen-related receptor α (ERRα)/peroxisome proliferator-activated receptor γ coactivator 1α (PGC-1α) complex, in turn increasing levels of the exercise-secreted factor FNDC5 in skeletal muscle and the hippocampus, whose cleavage products provide beneficial effects in the hippocampus by increasing BDNF gene expression. While future research should determine whether the FNDC5 cleavage-product was produced locally in hippocampal neurons or was secreted into the circulation, this finding eloquently displays one mechanism responsible for brain health benefits following exercise. Similarly, work by van Praag and colleagues suggests that exercise or pharmacological activation of AMP-activated protein kinase (AMPK) in skeletal muscle enhances indices of learning and memory, neurogenesis, and gene expression related to mitochondrial function in the hippocampus ( Kobilo et al. 2011 , 2014 ; Guerrieri and van Praag 2015 ).
Insulin-like growth factor 1 (IGF-1), is central to many exercise-induced adaptations in the brain. Like BDNF, physical activity increases circulatory IGF-1 levels and both exercise and infusion of IGF-1 increase BrdU + cell number and survivability in the hippocampus ( Trejo et al. 2001 ). Similarly, the protective effects of exercise on various brain lesions are nullified by anti-IGF-1 antibody ( Carro et al. 2001 ).
In 1979, Greist et al. (1979) provided evidence that running reduced depression symptoms similarly to psychotherapy. However, the precise mechanisms by which exercise prevents and/or treats depression remain largely unknown. Of the proposed mechanisms, increases in the availability of brain neurotransmitters and neurotrophic factors (e.g., BDNF, dopamine, glutamate, norepinephrine, serotonin) are perhaps the best studied. For example, tyrosine hydroxylase (TH) activity, the rate-limiting enzyme in dopamine formation, in the striatum, an area of the brain's reward system, is increased following 7 days of treadmill running in an intensity-dependent manner ( Hattori et al. 1994 ). Voluntary wheel running is also highly rewarding in rats, and voluntary wheel running in rats lowers the motivation to self-administer cocaine, suggesting exercise may be a viable strategy in the fight against drug addiction ( Larson and Carroll 2005 ).
Similar to the above examples, secreted factors from skeletal muscle have been linked to the regulation of depression. Agudelo et al. (2014) showed that exercise training in mice and humans, and overexpression of skeletal muscle PGC-1α1, leads to robust increases in kynurenine amino transferase (KAT) expression in skeletal muscle, an enzyme whose activity protects from stress-induced increases in depression in the brain by converting kynurenine into kynurenic acid. Additionally, overexpression of PGC-1α1 in skeletal muscle left mice resistant to stress, as evaluated by various behavioral assays indicative of depression ( Agudelo et al. 2014 ). Simultaneously, they report gene expression related to synaptic plasticity in the hippocampus, such as BDNF and CamkII, were unaffected by chronic mild stress compared to wild-type mice. Collectively, these findings suggest exercise-induced increases in skeletal muscle PGC-1α1 may be an important regulator of KAT expression in skeletal muscle, which, via modulation in plasma kynurenine levels, may alleviate stress-induced depression and promote hippocampal neuronal plasticity.
TYPE 2 DIABETES, MITOCHONDRIA, AND EXERCISE
T2d predictions show a pandemic.
In a 2001 Diabetes Care article ( Boyle et al. 2001 ), investigators at the U.S. Centers for Disease Control (CDC) predicted 29 million U.S. cases of T2D would be present in 2050. Unfortunately, the 2001 prediction of 29 million was reached in 2012! For 2012, the American Diabetes Association reported that 29 million Americans had diagnosed and undiagnosed T2D, which was 9% of the American population ( Dwyer-Lindgren et al. 2016 ). More rapid increases in T2D are now predicted by the CDC than in the previous estimate. The CDC now predicts a doubling or tripling in T2D in 2050. The tripling would mean that one out of three U.S. adults would have T2D in their lifetime by 2050 ( Boyle et al. 2010 ), which would be >100 million U.S. cases. The International Diabetes Federation (IDF) reports T2D cases worldwide. In 2015, the IDF reported that 344 and 416 million North American (including Caribbean) and worldwide adults, respectively, had T2D. Furthermore, the IDF predicts for 2040 that 413 and 642 million, respectively, will have T2D. In sum, T2D is now pandemic, and the pandemic will increase in numbers without current apparent action within the general public.
Type 2 Diabetes Prevalence Is Based on a Strong Genetic Predisposition
The Framingham study found that T2D risk in offspring was 3.5-fold and sixfold higher for a single and two diabetic parent(s), respectively, as compared to nondiabetic offspring ( Meigs et al. 2000 ). Thus, T2D is gene-based.
Noncoding regions of the human genome contain >90% of the >100 variants associated with both T2D and related traits that were observed in genome-wide association studies ( Scott et al. 2016 ). Another 2016 paper ( Kwak and Park 2016 ) lists at least 75 independent genetic loci that are associated with T2D. Taken together, T2D is a complex genetic disease ( Scott et al. 2016 ).
Type 2 Diabetes Is Modulated by Lifestyle, with Exercise as the More Powerful Lifestyle Factor
Three large-scale epidemiological studies have been performed on prediabetics, each in a different geographical location. The first study, and only study to have separate study arms for diet and exercise, was in China. The pure exercise intervention group had a 46% reduction in the onset of T2D, relative to the nontreated group, after 6 yr of the study ( Pan et al. 1997 ). Diet alone reduced T2D by 31% in the Chinese study. The second study on T2D was the Finnish Diabetes Prevention Study. It found a 58% reduction in T2D in the lifestyle intervention (combined diet and exercise) in its 522 prediabetic subjects after a mean study duration of 3.2 yr ( Tuomilehto et al. 2001 ). The latest of the three studies was in the U.S. Diabetes Prevention Program. The large randomized trial ( n = 3150 prediabetics) was stopped after 2.8 yr, because of harm to the control group. T2D prevalence in the high-risk adults was reduced by 58% with intensive lifestyle (diet and exercise) intervention, whereas the drug arm (metformin) of the study only reduced T2D by 31%, both compared to the noninnervation group ( Knowler et al. 2002 ). Thus, if differences in genetics in the above three differing ethnicities are not a factor, combined exercise and diet remain more effective in T2D prevention than the drug metformin two decades ago.
Exercise Increases Glucose by Signaling Independent of the Insulin Receptor
A single exercise bout increases glucose uptake by skeletal muscle, sidestepping the insulin receptor and thus insulin resistance in T2D patients ( Holloszy and Narahara 1965 ; Goodyear and Kahn 1998 ; Holloszy 2005 ). After insulin binding to its receptor, insulin initiates a downstream signaling cascade of tyrosine autophosphorylation of insulin receptor, insulin receptor substrate 1 (IRS-1) binding and phosphorylation, activation of a PI3K-dependent pathway, including key downstream regulators protein kinase B (Akt) and the Akt substrate of 160 kDa (AS160), ultimately promoting glucose transporter 4 (GLUT4) translocation to the plasma membrane ( Rockl et al. 2008 ; Stanford and Goodyear 2014 ). Despite normal GLUT4 levels, insulin fails to induce GLUT4 translocation in T2D ( Zierath et al. 2000 ). However, exercise activates a downstream insulin-signaling pathway at AS160 and TBC1 domain family member 1 (TBC1D1) ( Deshmukh et al. 2006 ; Maarbjerg et al. 2011 ), facilitating GLUT4 expression translocation to the plasma membrane independent of the insulin receptor. We contend that exercise could be considered as a very powerful tool to primarily attenuate the T2D pandemic.
Complex Biology of T2D Interactions with the Complex Biology of Exercise
An important consideration from the above is that T2D is such a genetically complex disease that a single gene has not been proven to be sufficiently causal to be effective, at this stage in time, to be a successful target for pharmacological treatment. The expectation for a single molecule target has been met for infectious diseases, which are often monogenic diseases. For example, a vaccine against smallpox was highly successful. Edward Jenner in 1796 produced the first successful vaccine. An important fact is that exercise is genetically complex. The literature allows us to speculate that exercise is at least as genetically complex as the approximately 75 genes associated with T2D ( Kwak and Park 2016 ). An example indicating that exercise is complex biology follows. RNA sequencing analysis of all 119 vastus lateralis muscle biopsies found that endurance training for 4 days/wk for 12 wk produced the differential expression of 3404 putative isoforms, belonging to 2624 different genes, many associated with oxidative ATP production in 23 women and men aged 29 yr old ( Lindholm et al. 2016 ). Our notion is that over 2600 genes suggests complex biology.
A “Case-Type” Study of the Molecular Underpinnings of Exercise, Mitochondria, and T2D Interactions
A PubMed search for the terms “diabetes mitochondria exercise molecular” elicited 74 papers. We arbitrarily selected some of the most recent 50 (spanning from mid-2014 into January 2017), with the assumption they would be representative of any other papers that we did not find in our search. Papers fell into our two arbitrary categories of single gene studies versus “omic”-type studies. First, subcategories of studies that develop themes will be arbitrarily presented.
Recent Studies Show Single Gene Manipulation Alters Mitochondrial Level and Running Performance
Numerous reports in the past couple of years observed that single gene manipulations increase mitochondrial gene expression and activity, which was also associated with increased exercise performance/capacity. A few of these are presented below:
- Irisin was shown to increase oxidative metabolism in myocytes and increase PGC-1α mRNA and protein ( Vaughan et al. 2014 ), which extends the first observation made earlier in adipose tissue by Spiegelman ( Bostrom et al. 2012 ).
- Patients with impaired glucose tolerance underwent low-intensity exercise training. Patients whose mitochondrial markers increased to levels that were measured in a separate cohort of nonexercised healthy individuals recovered normal glucose tolerance ( Osler et al. 2015 ). In opposition, those patients whose mitochondria markers did not improve, remained with impaired glucose tolerance.
- In 2003, muscle PGC-1α mRNA was shown to be induced by endurance-exercise training in human skeletal muscle ( Short et al. 2003 ). PGC-1α was shown to have multiple isoforms ( Lin et al. 2002 ). After a 60-min cycling bout, human vastus lateralis biopsies were taken from both sexes in their mid-20s. Additional biopsies were taken 30 min, and at 2, 6, and 24 hr postexercise. At 30 min postexercise, PGC-1α-ex1b mRNA and PGC-1α mRNA increased 468- and 2.4-fold, respectively, whereas PGC-1α-ex1b protein and PGC-1α protein increased 3.1-fold and no change, respectively. Gidlund et al. (2015 ) interprets the above data as implying PGC-1α-ex1b could be responsible for other changes that have previously been recorded before the increase in total PGC-1α postexercise.
- Mice with knockout of the kinin B1 receptor gene had higher mitochondrial DNA quantification and of mRNA levels of genes related to mitochondrial biogenesis in soleus and gastrocnemius muscles and had higher exercise times to exhaustion, but did not have higher VO 2max ( Reis et al. 2015 ).
- Mice do not normally express cholesteryl ester transfer protein (CETP), which is a lipid transfer protein that shuttles lipids between serum lipoproteins and tissues. Overexpression of CETP in mice after 6 wk on a high-fat diet increased treadmill running duration and distance, mitochondrial oxidation of glutamate/malate, but not palmitoylcarnitine oxidation, and doubled PGC-1α mRNA concentration ( Cappel et al. 2015 ).
- The myokine musclin is a peptide secreted from exercising muscle during treadmill running. Removal of musclin release during running results in lowered VO 2max , lower skeletal muscle mitochondrial content and respiratory complex protein expression, and reduced exercise tolerance ( Subbotina et al. 2015 ).
- Lactate dehydrogenase B (LDHB), which produces pyruvate from lactate, was overexpressed in mouse skeletal muscle. Increases in markers of skeletal muscle mitochondria were associated with increased running distance in a progressive speed test, and increased peak VO 2 ( Liang et al. 2016 ).
- Another example of endurance-type exercise adaptations is the 2016 paper that transcription factor EB (TFEB) regulates metabolic flexibility in skeletal muscle independent of PGC-1α during endurance-type exercise ( Mansueto et al. 2017 ). Lack of metabolic flexibility, termed “metabolic inflexibility,” is important because it is common in T2D. One definition of metabolic inflexibility is its inability to rapidly switch between glucose and fatty acid substrates for ATP production when nutrient availability changes from high blood glucose levels immediately after a meal to decreasing below 100 mg/dl when not eating for hours after a meal. A clinical consequence of T2D-induced metabolic inflexibility is prolonged periods of hyperglycemia, because skeletal muscle is more insulin insensitive in T2D. In contrast, after sufficient endurance exercise, skeletal muscle increases its insulin sensitivity by a second pathway that is independent of proximal postreceptor insulin signaling (see Stephenson et al. 2014 for further discussion).
Studies Showing that Manipulation of One Signaling Molecule Does Not Alter Expression of All Genes with Mitochondrial Functions Found in Skeletal Muscles of Wild-Type Animals to Exercise Training
A 2010 review article ( Lira et al. 2010 ) concludes from gene-deletion studies that p38γ MAPK/PGC-1α signaling controls mitochondrial biogenesis’ adaptation to endurance exercise in skeletal muscle. Two studies do not completely agree with the conclusion in the review article. The Pilegaard laboratory published a 2008 study ( Leick et al. 2008 ) that did not confirm their hypothesis that PGC-1α was required for every metabolic protein adaptive increase after endurance-exercise training by skeletal muscle. They reported that PGC-1α was not required for endurance-training-induced increases in ALAS1, COXI, and cytochrome c expression ( Leick et al. 2008 ). Their interpretation, at that time, was that molecules other than PGC-1α can exert exercise-induced mitochondrial adaptations. A second study published in 2012 rendered a similar verdict. A 12-day program of endurance training led to the middle portion of the gastrocnemius muscle demonstrating a similar 60% increase in mitochondrial density in both wild-type and PGC-1α muscle-specific knockout mice (Myo-PGC-1αKO) ( Rowe et al. 2012 ). The paper concludes that PGC-1α is dispensable for endurance-exercise’s induction of skeletal muscle mitochondrial adaptations.
Exercise signaling targets have actions that are independent of PGC-1α, which is specific to endurance exercise. In 2002, two groups identified PGC-1β, a transcriptional coactivator closely related to PGC-1α ( Kressler et al. 2002 ; Lin et al. 2002 ). Later in 2012, the PGC-1α4 variant of PGC-1α was found to induce skeletal muscle hypertrophy and strength ( Ruas et al. 2012 ). The importance of the finding of a PGC-1α variant is that it partially explains the phenotypic variation for differing types of exercise. Since the 1970s ( Holloszy and Booth 1976 ), it has been appreciated that the biochemical and anatomical observations between endurance and resistance differed. For example, Holloszy and Booth (1976) noted in 1976 that, whereas endurance-type exercise markedly increased skeletal muscle mitochondrial density with very minor increases in muscle fiber diameter, strength-type exercise, in contrast, increased muscle fiber diameter without increases in skeletal muscle mitochondrial density. Taken together, a drug specific for PGC-1α will not likely mimic separate physical training for endurance, strength/resistance, and coordination types of exercise in the same subject. Thus, the common usage of the term exercise capacity is a misnomer because endurance training and resistance training were shown to have different exercise capacity phenotypes very long ago.
In a 2015 Diabetes paper ( Wong et al. 2015 ), Muoio’s laboratory concluded that changes in glucose tolerance and total body fat depended upon how much energy is expended in contracting muscle rather than muscle mitochondrial content or substrate selection. A finding to support the previous sentence was the glucose tolerance tests (GTTs). MCK-PGC-1α mice and their nontransgenic (NT) littermates were not different in GTT, with both being the most glucose intolerant after 10 wk of high-fat feeding. Adding 10 wk of voluntary wheel running to the two high-fat-feed groups during the next 10-wk period (weeks 11–20 of the experiment) lowered the glucose intolerance, and then during weeks 21–30 of the experiment, glucose intolerance was further lowered by adding 25% caloric restriction with the high-fat food and running during the final 10 wk. The percentage weight lost after 30 wk of high-fat feeding was positively related to greater running distances. No single front-runner gene candidate could be identified by principle component analysis. Taken together, the paper suggests “doubts” that pharmacological exercise mimetics that increase muscle oxidative capacity will be effective antiobesity and/or antidiabetic agents. Rather, Muoio and investigators suggest energy expenditure by muscle contraction induces localized shifts in energy balance inside the muscle fiber, which then initiates a broad network of metabolic intermediates regulating nutrient sensing and insulin action. A further discussion of complex biology produced by polygenicity continues next.
POLYGENICITY OF EXERCISE LEADS TO COMPLEX MULTISYSTEM RESPONSES TO IMPROVE HEALTH OUTCOMES
Multiples tissues, organs, and systems are influenced by physical activity, or the lack thereof ( Table 2 ).
Worsening of maximal functioning in selected major organ/tissue/systems that are caused by the lack of physical activity with growth, maturation, and aging
| Site | Organ/tissue/system loses designated function, most with aging after maturation |
|---|---|
| Brain | Specific types of cognition |
| Brain | Motor coordination and balance |
| Heart | Maximal pumping volume/minute |
| Peripheral circulation | Maximal capacity to supply blood to working muscles |
| Peripheral circulation | Prevention of capillary rarefaction in feet |
| Skeletal muscle | Less mass and strength |
| Skeletal muscle | Lower insulin sensitivity |
| Pancreas | Loss of β cells |
| Aerobic capacity | Lower |
| Bone | Less mass and strength |
| Liver | Excessive fat storage |
The higher their maximal function is before the end of each item’s maturation, the longer chances are that the quality of life will remain optimal. The breadth of the list implies that a single molecular target will not substitute for appropriate daily physical activity to prevent the loss of all listed items.
To present one extreme, that most will agree, one molecule will not describe the 1000s of molecules adapting to aerobic, resistance, and coordination exercise training. On the opposite extreme, many could likely agree that usage of the various “omics” underlying all adaptations to physical activity will differ (i.e., not be identical in most aspects) among the next list: various cell types within a tissue/organ, tissues/organs, and various intensities of physical activity (i.e., the thresholds among gene responses for health benefits will differ because of the presence of responders and nonresponders, or protein isoform type); during various types cycling (circadian or menstrual); postprandial versus fasting between meals; male and female; child, adult, and the elderly; trained and untrained; aerobic- and resistance-exercise types; and so forth. Others have repetitively written that only ∼59% of the risk reduction for all forms of CVD have been shown to be caused by effects through traditional factors ( Mora et al. 2007 ; Joyner and Green 2009 ). Thus, we pose the next question: what is the identity of all molecules in the yet-to-be-discovered gap between our knowledge of single gene functions and the totality of personalized prescription of physical activity to maximize the period of life free of any chronic disease, termed health span?
While approaches using single-gene manipulations are valuable tools, research must also focus on integrating exercise-responsive molecules into networks that maintain or improve health. This process will reveal complex, multisystem, polygenic networking essential for the advancement of many goals pertaining to exercise physiology, such as tailoring exercise prescriptions and implementing personalized medicine. One example is the developing myokine network with auto-, para-, and endocrine molecules. The first myokine interleukin (IL)-6 began to be described as early as 1994 by the Pedersen laboratory ( Ullum et al. 1994 ), with a history of its development as the first exercise myokine recounted in 2007 ( Pedersen et al. 2007 ). Since their discovery, myokine action within and at a distance from their origins in skeletal muscle have been increasingly studied, as schematically illustrated by Schnyder and Handschin (2015) ( Fig. 2 ).

Figure provides an illustration of myokine production by skeletal muscle for actions within or at a distance. Myokine release promotes a high degree of intertissue cross talk. CNTF, Ciliary neurotrophic factor; OSM, oncostatin M; IL, interleukin; BDNF, brain-derived neurotrophic factor; VEGF, vascular endothelial growth factor. (From Schnyder and Handschin 2015 ; reprinted, with permission, courtesy of PMC Open Access.)
Similarly, maximal aerobic exercise is accompanied by tremendous stress on many systems, yet whole-body homeostasis is remarkably maintained. For example, world-class endurance athletes can increase whole-body energy production well over 20-fold ( Joyner and Coyle 2008 ), whereas maintaining blood glucose concentrations at resting levels ( Wasserman 2009 ). Intuitively, such effort would require sophisticated interorgan cross talk and polygenic integration of numerous functions.
Exercise Provides Too Many Benefits to “Fit into a Single Pill”
Despite the well-known benefits of exercise, most adults and many children lead relatively sedentary lifestyles and are not active enough to achieve the health benefits of exercise ( Warburton et al. 2006 ; Fried 2016 ). Accelerometry measurements suggest that >90% of U.S. individuals >12 yr of age and ∼50% of children aged 6–11 yr old fail to meet U.S. Federal physical activity guidelines ( Troiano et al. 2008 ). Given this incredibly low compliance, the identification of genetic and/or orally active agents that mimic the effects of endurance exercise might have high appeal for a majority of sedentary individuals. This high appeal has led to recent identification/development of exercise “mimetics.” In 2009, we set criteria for proper usage of the term “exercise mimetic,” based upon its common usage ( Booth and Laye 2009 ). We gave the Oxford English Dictionary’s definition of mimetic, “A synthetic compound that produces the same (or a very similar) effect as another (especially a naturally occurring) compound.” While many exercise “mimetics” activate signaling pathways commonly associated with muscle endurance, these agents have not completely mimicked all effects for all types of exercise. For example, the AMPK activator 5-aminoimidazole-4-carboxamide ribonucleotide (AICAR), when given daily to rats over a 5-wk-period, did not increase maximal oxygen consumption (VO 2peak ) in the sedentary group of rats that were forced to run to VO 2peak on treadmills, as compared to sedentary rats receiving the vehicle ( Toedebusch et al. 2016 ). Thus, in our opinion, the published claim ( Narkar et al. 2008 ) that AICAR is an exercise mimetic is invalidated because it did not increase VO 2peak . While these agents may undoubtedly have specific health benefits, it is currently impractical to assume that all of the benefits of exercise can be replaced by “exercise mimetics.”
CONCLUDING REMARKS
Exercise is a powerful tool in the fight to prevent and treat numerous chronic diseases ( Table 1 ). Given its whole-body, health-promoting nature, the integrative responses to exercise should surely attract a great detail of interest as the notion of “exercise is medicine” continues to its integration into clinical settings.
ACKNOWLEDGMENTS
The authors disclose no conflicts of interest. Partial funding for this project was obtained from grants awarded to G.N.R. (AHA 16PRE2715005).
Editors: Juleen R. Zierath, Michael J. Joyner, and John A. Hawley
Additional Perspectives on The Biology of Exercise available at www.perspectivesinmedicine.org
- Agudelo LZ, Femenia T, Orhan F, Porsmyr-Palmertz M, Goiny M, Martinez-Redondo V, Correia JC, Izadi M, Bhat M, Schuppe-Koistinen I, et al. 2014. Skeletal muscle PGC-1α1 modulates kynurenine metabolism and mediates resilience to stress-induced depression . Cell 159 : 33–45. [ PubMed ] [ Google Scholar ]
- Astrand PO. 1956. Human physical fitness with special reference to sex and age . Physiol Rev 36 : 307–335. [ PubMed ] [ Google Scholar ]
- Bacon AP, Carter RE, Ogle EA, Joyner MJ. 2013. VO 2max trainability and high intensity interval training in humans: A meta-analysis . PLoS ONE 8 : e73182. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Beier M, Bombardier CH, Hartoonian N, Motl RW, Kraft GH. 2014. Improved physical fitness correlates with improved cognition in multiple sclerosis . Arch Phys Med Rehabil 95 : 1328–1334. [ PubMed ] [ Google Scholar ]
- Berchtold NC, Chinn G, Chou M, Kesslak JP, Cotman CW. 2005. Exercise primes a molecular memory for brain-derived neurotrophic factor protein induction in the rat hippocampus . Neuroscience 133 : 853–861. [ PubMed ] [ Google Scholar ]
- Bielak AA, Cherbuin N, Bunce D, Anstey KJ. 2014. Preserved differentiation between physical activity and cognitive performance across young, middle, and older adulthood over 8 years . J Gerontol B Psychol Sci Soc Sci 69 : 523–532. [ PubMed ] [ Google Scholar ]
- Bjerring P, Arendt-Nielsen L. 1990. Inhibition of histamine skin flare reaction following repeated topical applications of capsaicin . Allergy 45 : 121–125. [ PubMed ] [ Google Scholar ]
- Blair SN, Kohl HW III, Paffenbarger RS Jr, Clark DG, Cooper KH, Gibbons LW. 1989. Physical fitness and all-cause mortality. A prospective study of healthy men and women . JAMA 262 : 2395–2401. [ PubMed ] [ Google Scholar ]
- Booth FW, Laye MJ. 2009. Lack of adequate appreciation of physical exercise’s complexities can preempt appropriate design and interpretation in scientific discovery . J Physiol 587 : 5527–5539. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Booth FW, Chakravarthy MV, Gordon SE, Spangenburg EE. 2002. Waging war on physical inactivity: Using modern molecular ammunition against an ancient enemy . J Appl Physiol (1985) 93 : 3–30. [ PubMed ] [ Google Scholar ]
- Booth FW, Roberts CK, Laye MJ. 2012. Lack of exercise is a major cause of chronic diseases . Compr Physiol 2 : 1143–1211. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Bostrom P, Wu J, Jedrychowski MP, Korde A, Ye L, Lo JC, Rasbach KA, Bostrom EA, Choi JH, Long JZ, et al. 2012. A PGC1-α-dependent myokine that drives brown-fat-like development of white fat and thermogenesis . Nature 481 : 463–468. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Boyle JP, Honeycutt AA, Narayan KM, Hoerger TJ, Geiss LS, Chen H, Thompson TJ. 2001. Projection of diabetes burden through 2050: Impact of changing demography and disease prevalence in the U.S . Diabetes Care 24 : 1936–1940. [ PubMed ] [ Google Scholar ]
- Boyle JP, Thompson TJ, Gregg EW, Barker LE, Williamson DF. 2010. Projection of the year 2050 burden of diabetes in the US adult population: Dynamic modeling of incidence, mortality, and prediabetes prevalence . Popul Health Metr 8 : 29. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Cappel DA, Lantier L, Palmisano BT, Wasserman DH, Stafford JM. 2015. CETP expression protects female mice from obesity-induced decline in exercise capacity . PLoS ONE 10 : e0136915. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Carro E, Trejo JL, Busiguina S, Torres-Aleman I. 2001. Circulating insulin-like growth factor I mediates the protective effects of physical exercise against brain insults of different etiology and anatomy . J Neurosci 21 : 5678–5684. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Cotman CW, Berchtold NC. 2002. Exercise: A behavioral intervention to enhance brain health and plasticity . Trends Neurosci 25 : 295–301. [ PubMed ] [ Google Scholar ]
- Creer DJ, Romberg C, Saksida LM, van Praag H, Bussey TJ. 2010. Running enhances spatial pattern separation in mice . Proc Natl Acad Sci 107 : 2367–2372. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Deshmukh A, Coffey VG, Zhong Z, Chibalin AV, Hawley JA, Zierath JR. 2006. Exercise-induced phosphorylation of the novel Akt substrates AS160 and filamin A in human skeletal muscle . Diabetes 55 : 1776–1782. [ PubMed ] [ Google Scholar ]
- Dwyer-Lindgren L, Mackenbach JP, van Lenthe FJ, Flaxman AD, Mokdad AH. 2016. Diagnosed and undiagnosed diabetes prevalence by county in the U.S., 1999–2012 . Diabetes Care 39 : 1556–1562. [ PubMed ] [ Google Scholar ]
- Fried LP. 2016. Interventions for human frailty: Physical activity as a model . Cold Spring Harb Perspect Med doi: 10.1101/cshperspect.a025916. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Gidlund EK, Ydfors M, Appel S, Rundqvist H, Sundberg CJ, Norrbom J. 2015. Rapidly elevated levels of PGC-1α-b protein in human skeletal muscle after exercise: Exploring regulatory factors in a randomized controlled trial . J Appl Physiol (1985) 119 : 374–384. [ PubMed ] [ Google Scholar ]
- Goodyear LJ, Kahn BB. 1998. Exercise, glucose transport, and insulin sensitivity . Annu Rev Med 49 : 235–261. [ PubMed ] [ Google Scholar ]
- Greenwood BN, Loughridge AB, Sadaoui N, Christianson JP, Fleshner M. 2012. The protective effects of voluntary exercise against the behavioral consequences of uncontrollable stress persist despite an increase in anxiety following forced cessation of exercise . Behav Brain Res 233 : 314–321. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Greist JH, Klein MH, Eischens RR, Faris J, Gurman AS, Morgan WP. 1979. Running as treatment for depression . Compr Psychiatry 20 : 41–54. [ PubMed ] [ Google Scholar ]
- Guerrieri D, van Praag H. 2015. Exercise-mimetic AICAR transiently benefits brain function . Oncotarget 6 : 18293–18313. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Gupta S, Rohatgi A, Ayers CR, Willis BL, Haskell WL, Khera A, Drazner MH, de Lemos JA, Berry JD. 2011. Cardiorespiratory fitness and classification of risk of cardiovascular disease mortality . Circulation 123 : 1377–1383. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Hattori S, Naoi M, Nishino H. 1994. Striatal dopamine turnover during treadmill running in the rat: Relation to the speed of running . Brain Res Bull 35 : 41–49. [ PubMed ] [ Google Scholar ]
- Holloszy JO. 2005. Exercise-induced increase in muscle insulin sensitivity . J Appl Physiol (1985) 99 : 338–343. [ PubMed ] [ Google Scholar ]
- Holloszy JO, Booth FW. 1976. Biochemical adaptations to endurance exercise in muscle . Annu Rev Physiol 38 : 273–291. [ PubMed ] [ Google Scholar ]
- Holloszy JO, Narahara HT. 1965. Studies of tissue permeability. X: Changes in permeability to 3-methylglucose associated with contraction of isolated frog muscle . J Biol Chem 240 : 3493–3500. [ PubMed ] [ Google Scholar ]
- Joyner MJ, Coyle EF. 2008. Endurance exercise performance: The physiology of champions . J Physiol 586 : 35–44. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Joyner MJ, Green DJ. 2009. Exercise protects the cardiovascular system: Effects beyond traditional risk factors . J Physiol 587 : 5551–5558. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Keller P, Vollaard NB, Gustafsson T, Gallagher IJ, Sundberg CJ, Rankinen T, Britton SL, Bouchard C, Koch LG, Timmons JA. 2011. A transcriptional map of the impact of endurance exercise training on skeletal muscle phenotype . J Appl Physiol (1985) 110 : 46–59. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Knowler WC, Barrett-Connor E, Fowler SE, Hamman RF, Lachin JM, Walker EA, Nathan DM. 2002. Reduction in the incidence of type 2 diabetes with lifestyle intervention or metformin . N Engl J Med 346 : 393–403. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Kobilo T, Yuan C, van Praag H. 2011. Endurance factors improve hippocampal neurogenesis and spatial memory in mice . Learn Mem 18 : 103–107. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Kobilo T, Guerrieri D, Zhang Y, Collica SC, Becker KG, van Praag H. 2014. AMPK agonist AICAR improves cognition and motor coordination in young and aged mice . Learn Mem 21 : 119–126. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Koch LG, Kemi OJ, Qi N, Leng SX, Bijma P, Gilligan LJ, Wilkinson JE, Wisloff H, Hoydal MA, Rolim N, et al. 2011. Intrinsic aerobic capacity sets a divide for aging and longevity . Circ Res 109 : 1162–1172. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Kodama S, Saito K, Tanaka S, Maki M, Yachi Y, Asumi M, Sugawara A, Totsuka K, Shimano H, Ohashi Y, et al. 2009. Cardiorespiratory fitness as a quantitative predictor of all-cause mortality and cardiovascular events in healthy men and women: A meta-analysis . JAMA 301 : 2024–2035. [ PubMed ] [ Google Scholar ]
- Kokkinos P, Myers J, Faselis C, Panagiotakos DB, Doumas M, Pittaras A, Manolis A, Kokkinos JP, Karasik P, Greenberg M, et al. 2010. Exercise capacity and mortality in older men: A 20-year follow-up study . Circulation 122 : 790–797. [ PubMed ] [ Google Scholar ]
- Kratz AL, Ehde DM, Bombardier CH. 2014. Affective mediators of a physical activity intervention for depression in multiple sclerosis . Rehabil Psychol 59 : 57–67. [ PubMed ] [ Google Scholar ]
- Kressler D, Schreiber SN, Knutti D, Kralli A. 2002. The PGC-1-related protein PERC is a selective coactivator of estrogen receptor α . J Biol Chem 277 : 13918–13925. [ PubMed ] [ Google Scholar ]
- Kwak SH, Park KS. 2016. Recent progress in genetic and epigenetic research on type 2 diabetes . Exp Mol Med 48 : e220. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Larson EB, Carroll ME. 2005. Wheel running as a predictor of cocaine self-administration and reinstatement in female rats . Pharmacol Biochem Behav 82 : 590–600. [ PubMed ] [ Google Scholar ]
- Leick L, Wojtaszewski JF, Johansen ST, Kiilerich K, Comes G, Hellsten Y, Hidalgo J, Pilegaard H. 2008. PGC-1α is not mandatory for exercise- and training-induced adaptive gene responses in mouse skeletal muscle . Am J Physiol Endocrinol Metab 294 : E463–E474. [ PubMed ] [ Google Scholar ]
- Liang X, Liu L, Fu T, Zhou Q, Zhou D, Xiao L, Liu J, Kong Y, Xie H, Yi F, et al. 2016. Exercise inducible lactate dehydrogenase B regulates mitochondrial function in skeletal muscle . J Biol Chem 291 : 25306–25318. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Lin J, Puigserver P, Donovan J, Tarr P, Spiegelman BM. 2002. Peroxisome proliferator-activated receptor γ coactivator 1 β (PGC-1β ), a novel PGC-1-related transcription coactivator associated with host cell factor . J Biol Chem 277 : 1645–1648. [ PubMed ] [ Google Scholar ]
- Lindholm ME, Giacomello S, Werne Solnestam B, Fischer H, Huss M, Kjellqvist S, Sundberg CJ. 2016. The impact of endurance training on human skeletal muscle memory, global isoform expression and novel transcripts . PLoS Genet 12 : e1006294. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Lira VA, Benton CR, Yan Z, Bonen A. 2010. PGC-1α regulation by exercise training and its influences on muscle function and insulin sensitivity . Am J Physiol Endocrinol Metab 299 : E145–E161. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Lynch WJ, Peterson AB, Sanchez V, Abel J, Smith MA. 2013. Exercise as a novel treatment for drug addiction: A neurobiological and stage-dependent hypothesis . Neurosci Biobehav Rev 37 : 1622–1644. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Maarbjerg SJ, Sylow L, Richter EA. 2011. Current understanding of increased insulin sensitivity after exercise—Emerging candidates . Acta Physiol (Oxf) 202 : 323–335. [ PubMed ] [ Google Scholar ]
- Mansueto G, Armani A, Viscomi C, D’Orsi L, De Cegli R, Polishchuk EV, Lamperti C, Di Meo I, Romanello V, Marchet S, et al. 2017. Transcription factor EB controls metabolic flexibility during exercise . Cell Metab 25 : 182–196. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Mattson MP. 2014. Interventions that improve body and brain bioenergetics for Parkinson’s disease risk reduction and therapy . J Parkinsons Dis 4 : 1–13. [ PubMed ] [ Google Scholar ]
- McKercher C, Sanderson K, Schmidt MD, Otahal P, Patton GC, Dwyer T, Venn AJ. 2014. Physical activity patterns and risk of depression in young adulthood: A 20-year cohort study since childhood . Soc Psychiatry Psychiatr Epidemiol 49 : 1823–1834. [ PubMed ] [ Google Scholar ]
- Meigs JB, Cupples LA, Wilson PW. 2000. Parental transmission of type 2 diabetes: The Framingham Offspring Study . Diabetes 49 : 2201–2207. [ PubMed ] [ Google Scholar ]
- Mokdad AH, Marks JS, Stroup DF, Gerberding JL. 2004. Actual causes of death in the United States, 2000 . JAMA 291 : 1238–1245. [ PubMed ] [ Google Scholar ]
- Mora S, Cook N, Buring JE, Ridker PM, Lee IM. 2007. Physical activity and reduced risk of cardiovascular events: Potential mediating mechanisms . Circulation 116 : 2110–2118. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Morris JN, Heady JA, Raffle PA, Roberts CG, Parks JW. 1953. Coronary heart-disease and physical activity of work . Lancet 265 : 1053–1057. [ PubMed ] [ Google Scholar ]
- Mura G, Moro MF, Patten SB, Carta MG. 2014. Exercise as an add-on strategy for the treatment of major depressive disorder: A systematic review . CNS Spectr 19 : 496–508. [ PubMed ] [ Google Scholar ]
- Myers J, Prakash M, Froelicher V, Do D, Partington S, Atwood JE. 2002. Exercise capacity and mortality among men referred for exercise testing . N Engl J Med 346 : 793–801. [ PubMed ] [ Google Scholar ]
- Narkar VA, Downes M, Yu RT, Embler E, Wang YX, Banayo E, Mihaylova MM, Nelson MC, Zou Y, Juguilon H, et al. 2008. AMPK and PPARδ agonists are exercise mimetics . Cell 134 : 405–415. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Neeper SA, Gomez-Pinilla F, Choi J, Cotman C. 1995. Exercise and brain neurotrophins . Nature 373 : 109. [ PubMed ] [ Google Scholar ]
- Nishijima T, Llorens-Martin M, Tejeda GS, Inoue K, Yamamura Y, Soya H, Trejo JL, Torres-Aleman I. 2013. Cessation of voluntary wheel running increases anxiety-like behavior and impairs adult hippocampal neurogenesis in mice . Behav Brain Res 245 : 34–41. [ PubMed ] [ Google Scholar ]
- Osler ME, Fritz T, Caidahl K, Krook A, Zierath JR, Wallberg-Henriksson H. 2015. Changes in gene expression in responders and nonresponders to a low-intensity walking intervention . Diabetes Care 38 : 1154–1160. [ PubMed ] [ Google Scholar ]
- Pan XR, Li GW, Hu YH, Wang JX, Yang WY, An ZX, Hu ZX, Lin J, Xiao JZ, Cao HB, et al. 1997. Effects of diet and exercise in preventing NIDDM in people with impaired glucose tolerance. The Da Qing IGT and Diabetes Study . Diabetes Care 20 : 537–544. [ PubMed ] [ Google Scholar ]
- Park H, Poo MM. 2013. Neurotrophin regulation of neural circuit development and function . Nat Rev Neurosci 14 : 7–23. [ PubMed ] [ Google Scholar ]
- Pedersen BK, Akerstrom TC, Nielsen AR, Fischer CP. 2007. Role of myokines in exercise and metabolism . J Appl Physiol (1985) 103 : 1093–1098. [ PubMed ] [ Google Scholar ]
- Pereira AC, Huddleston DE, Brickman AM, Sosunov AA, Hen R, McKhann GM, Sloan R, Gage FH, Brown TR, Small SA. 2007. An in vivo correlate of exercise-induced neurogenesis in the adult dentate gyrus . Proc Natl Acad Sci 104 : 5638–5643. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Peterson AB, Hivick DP, Lynch WJ. 2014. Dose-dependent effectiveness of wheel running to attenuate cocaine-seeking: Impact of sex and estrous cycle in rats . Psychopharmacology (Berl) 231 : 2661–2670. [ PubMed ] [ Google Scholar ]
- Reis FC, Haro AS, Bacurau AV, Hirabara SM, Wasinski F, Ormanji MS, Moreira JB, Kiyomoto BH, Bertoncini CR, Brum PC, et al. 2015. Deletion of kinin B2 receptor alters muscle metabolism and exercise performance . PLoS ONE 10 : e0134844. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Rockl KS, Witczak CA, Goodyear LJ. 2008. Signaling mechanisms in skeletal muscle: Acute responses and chronic adaptations to exercise . IUBMB Life 60 : 145–153. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Ross R, de Lannoy L, Stotz PJ. 2015. Separate effects of intensity and amount of exercise on interindividual cardiorespiratory fitness response . Mayo Clin Proc 90 : 1506–1514. [ PubMed ] [ Google Scholar ]
- Rowe GC, El-Khoury R, Patten IS, Rustin P, Arany Z. 2012. PGC-1α is dispensable for exercise-induced mitochondrial biogenesis in skeletal muscle . PLoS ONE 7 : e41817. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Ruas JL, White JP, Rao RR, Kleiner S, Brannan KT, Harrison BC, Greene NP, Wu J, Estall JL, Irving BA, et al. 2012. A PGC-1α isoform induced by resistance training regulates skeletal muscle hypertrophy . Cell 151 : 1319–1331. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Ruegsegger GN, Toedebusch RG, Braselton JF, Childs TE, Booth FW. 2017. Left ventricle transcriptomic analysis reveals connective tissue accumulation associates with initial age-dependent decline in VO 2peak from its lifetime apex . Physiol Genomics 49 : 53–66. [ PubMed ] [ Google Scholar ]
- Sarzynski MA, Ghosh S, Bouchard C. 2016. Genomic and transcriptomic predictors of response levels to endurance exercise training . J Physiol 10.1113/JP272559. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Schneider J. 2013. Age dependency of oxygen uptake and related parameters in exercise testing: An expert opinion on reference values suitable for adults . Lung 191 : 449–458. [ PubMed ] [ Google Scholar ]
- Schnyder S, Handschin C. 2015. Skeletal muscle as an endocrine organ: PGC-1α, myokines and exercise . Bone 80 : 115–125. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Schoenfeld TJ, Rada P, Pieruzzini PR, Hsueh B, Gould E. 2013. Physical exercise prevents stress-induced activation of granule neurons and enhances local inhibitory mechanisms in the dentate gyrus . J Neurosci 33 : 7770–7777. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Schuch FB, Vancampfort D, Sui X, Rosenbaum S, Firth J, Richards J, Ward PB, Stubbs B. 2016. Are lower levels of cardiorespiratory fitness associated with incident depression? A systematic review of prospective cohort studies . Prev Med 93 : 159–165. [ PubMed ] [ Google Scholar ]
- Scott LJ, Erdos MR, Huyghe JR, Welch RP, Beck AT, Wolford BN, Chines PS, Didion JP, Narisu N, Stringham HM, et al. 2016. The genetic regulatory signature of type 2 diabetes in human skeletal muscle . Nat Commun 7 : 11764. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Short KR, Vittone JL, Bigelow ML, Proctor DN, Rizza RA, Coenen-Schimke JM, Nair KS. 2003. Impact of aerobic exercise training on age-related changes in insulin sensitivity and muscle oxidative capacity . Diabetes 52 : 1888–1896. [ PubMed ] [ Google Scholar ]
- Slentz CA, Aiken LB, Houmard JA, Bales CW, Johnson JL, Tanner CJ, Duscha BD, Kraus WE. 2005. Inactivity, exercise, and visceral fat. STRRIDE: A randomized, controlled study of exercise intensity and amount . J Appl Physiol (1985) 99 : 1613–1618. [ PubMed ] [ Google Scholar ]
- Slentz CA, Houmard JA, Kraus WE. 2007. Modest exercise prevents the progressive disease associated with physical inactivity . Exerc Sport Sci Rev 35 : 18–23. [ PubMed ] [ Google Scholar ]
- Stanford KI, Goodyear LJ. 2014. Exercise and type 2 diabetes: Molecular mechanisms regulating glucose uptake in skeletal muscle . Adv Physiol Educ 38 : 308–314. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Stephenson EJ, Smiles W, Hawley JA. 2014. The relationship between exercise, nutrition and type 2 diabetes . Med Sport Sci 60 : 1–10. [ PubMed ] [ Google Scholar ]
- Subbotina E, Sierra A, Zhu Z, Gao Z, Koganti SR, Reyes S, Stepniak E, Walsh SA, Acevedo MR, Perez-Terzic CM, et al. 2015. Musclin is an activity-stimulated myokine that enhances physical endurance . Proc Natl Acad Sci 112 : 16042–16047. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Tian Q, Erickson KI, Simonsick EM, Aizenstein HJ, Glynn NW, Boudreau RM, Newman AB, Kritchevsky SB, Yaffe K, Harris TB, et al. 2014. Physical activity predicts microstructural integrity in memory-related networks in very old adults . J Gerontol A Biol Sci Med Sci 69 : 1284–1290. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Timmons JA, Knudsen S, Rankinen T, Koch LG, Sarzynski M, Jensen T, Keller P, Scheele C, Vollaard NB, Nielsen S, et al. 2010. Using molecular classification to predict gains in maximal aerobic capacity following endurance exercise training in humans . J Appl Physiol (1985) 108 : 1487–1496. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Toedebusch RG, Ruegsegger GN, Braselton JF, Heese AJ, Hofheins JC, Childs TE, Thyfault JP, Booth FW. 2016. AMPK agonist AICAR delays the initial decline in lifetime-apex VO 2peak , while voluntary wheel running fails to delay its initial decline in female rats . Physiol Genomics 48 : 101–115. [ PubMed ] [ Google Scholar ]
- Trejo JL, Carro E, Torres-Aleman I. 2001. Circulating insulin-like growth factor I mediates exercise-induced increases in the number of new neurons in the adult hippocampus . J Neurosci 21 : 1628–1634. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Troiano RP, Berrigan D, Dodd KW, Masse LC, Tilert T, McDowell M. 2008. Physical activity in the United States measured by accelerometer . Med Sci Sports Exerc 40 : 181–188. [ PubMed ] [ Google Scholar ]
- Tuomilehto J, Lindstrom J, Eriksson JG, Valle TT, Hamalainen H, Ilanne-Parikka P, Keinanen-Kiukaanniemi S, Laakso M, Louheranta A, Rastas M, et al. 2001. Prevention of type 2 diabetes mellitus by changes in lifestyle among subjects with impaired glucose tolerance . N Engl J Med 344 : 1343–1350. [ PubMed ] [ Google Scholar ]
- Ullum H, Haahr PM, Diamant M, Palmo J, Halkjaer-Kristensen J, Pedersen BK. 1994. Bicycle exercise enhances plasma IL-6 but does not change IL-1α, IL-1β, IL-6, or TNF-α pre-mRNA in BMNC . J Appl Physiol (1985) 77 : 93–97. [ PubMed ] [ Google Scholar ]
- van Praag H, Kempermann G, Gage FH. 1999. Running increases cell proliferation and neurogenesis in the adult mouse dentate gyrus . Nat Neurosci 2 : 266–270. [ PubMed ] [ Google Scholar ]
- Vaughan RA, Gannon NP, Barberena MA, Garcia-Smith R, Bisoffi M, Mermier CM, Conn CA, Trujillo KA. 2014. Characterization of the metabolic effects of irisin on skeletal muscle in vitro . Diabetes Obes Metab 16 : 711–718. [ PubMed ] [ Google Scholar ]
- Warburton DE, Nicol CW, Bredin SS. 2006. Health benefits of physical activity: The evidence . CMAJ 174 : 801–809. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Wasserman DH. 2009. Four grams of glucose . Am J Physiol Endocrinol Metab 296 : E11–E21. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Widenfalk J, Olson L, Thoren P. 1999. Deprived of habitual running, rats downregulate BDNF and TrkB messages in the brain . Neurosci Res 34 : 125–132. [ PubMed ] [ Google Scholar ]
- Wong KE, Mikus CR, Slentz DH, Seiler SE, DeBalsi KL, Ilkayeva OR, Crain KI, Kinter MT, Kien CL, Stevens RD, et al. 2015. Muscle-specific overexpression of PGC-1α does not augment metabolic improvements in response to exercise and caloric restriction . Diabetes 64 : 1532–1543. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Wrann CD, White JP, Salogiannnis J, Laznik-Bogoslavski D, Wu J, Ma D, Lin JD, Greenberg ME, Spiegelman BM. 2013. Exercise induces hippocampal BDNF through a PGC-1α/FNDC5 pathway . Cell Metab 18 : 649–659. [ PMC free article ] [ PubMed ] [ Google Scholar ]
- Zierath JR, Krook A, Wallberg-Henriksson H. 2000. Insulin action and insulin resistance in human skeletal muscle . Diabetologia 43 : 821–835. [ PubMed ] [ Google Scholar ]
- Zlebnik NE, Anker JJ, Carroll ME. 2012. Exercise to reduce the escalation of cocaine self-administration in adolescent and adult rats . Psychopharmacology 224 : 387–400. [ PMC free article ] [ PubMed ] [ Google Scholar ]
Healthy Lifestyle and Eating Essay
- To find inspiration for your paper and overcome writer’s block
- As a source of information (ensure proper referencing)
- As a template for you assignment
Healthy eating is the process of keeping the body clean, strong, and healthy at all times (Allen, 1926). Healthy living, on the other hand, means that one should be able to eat the right food, get enough exercise, and maintain cleanliness (James, 1907). Unfortunately, many people do not keep track of these requirements. Thus, they end up with serious health problems, which can be difficult to treat. Prevention of these problems can be accomplished through maintaining a healthy lifestyle. Such a lifestyle is achievable by eating the right food and adhering to all the requirements of healthy living.
The human body needs a balanced diet, which includes enough minerals, fats, vitamins, fiber, and carbohydrates (Albrecht, 1932). These substances are required by the body to facilitate the growth and functioning of body tissues. Low energy foods such as vegetables and fruits have small amounts of calories per unit volume of food. Therefore, it is advisable to eat this combination of foods in large volumes as it contains fewer calories, but has nutrients that are essential for optimal body functionality. Incidentally, one should take food that is free from unhealthy fats, but should ensure that whole grains and proteins go alongside fruits and vegetables.
Apart from choosing the best foods for the body, it is also advisable that people should maintain moderate quantities of food intake. For instance, it is prudent to eat less of unhealthy foods such as refined sugar and saturated fats and more of healthy foods such as vegetables and fruits. This pattern of eating has massive health benefits to its adherents. As such, people should strive to develop good eating habits that can sustain them throughout their lives.
Further, it is recommended that one should eat a heavy breakfast an hour after waking up. The breakfast needs to consist of carbohydrates, healthy fats, and proteins in balanced proportions. It should then be followed by light meals throughout the day. This requirement is important since breakfast helps to initiate the body’s metabolism. The light and healthy meals thereafter help maintain a high body energy level that keeps one active throughout the day (Allen, 1926). People should avoid eating late at night. Early dinners are advisable followed by an average of 15 hours of no food until breakfast time the next morning. Past studies show that this pattern helps regulate body weight (James, 1907).
People who are diagnosed with lifestyle diseases such as anemia, high blood pressure, and diabetes among others are advised to follow diets that are rich in fruits and vegetable content (Allen, 1926). Depending on the stage of illness, such people should strictly watch what they eat. For example, high blood pressure patients should cut down on sodium, which is mainly found in salt. They should also avoid foods that have high cholesterol and saturated fats since diets of this sort prompt a high risk of artery clogging. Consequently, it increases the risk of heart attacks and blood vessel diseases (Albrecht, 1932). Further, they need to control the amount of carbohydrates they take.
Carbohydrates should only account for 50% of their daily calories (Allen, 1926). Finally, they are discouraged from foods with a high phosphorous content since they may lead to bone diseases (Allen, 1926). Overweight people constitute another special needs group. They should reduce weight to be healthy. Consequently, they need at least 30 minutes of rigorous physical exercise everyday and a lean diet.
In conclusion, all these groups of people should increase their water intake. Water is essential in the human body since it facilitates the regulation of all body functions. As such, it enhances body health. In this regard, people should strive to take at least eight glasses per day. Apparently, healthy living calls for discipline and commitment. If people foster these two values in the lifestyles, the world will be full of healthy people.
Albrecht, Arthur E. (1932). About foods and markets : A teachers’ handbook and consumers’ guide . New York City, NY: Columbia University. Web.
Allen, Ida C. (1926). Your foods and you or the role of diet . Garden City, NY: Doubleday Page & Company. Web.
James F. (1907). How we are fed: A geographical reader . New York, NY: Macmillan. Web.
- Analyzing Personal Diet and Intake Pattern
- The Concept of Carbohydrates
- Analysis of Breakfast for School Children in USA, UK, Finland and Singapore
- Diet and Nutrition: European Diabetes
- Obesity: the Public Health Challenge of Our Time
- Spoilage Device: Forget Expiration Dates
- "Salt, Sugar and Fat" a Book by Michael Moss
- Iron Deficiency Effects and Management
- Chicago (A-D)
- Chicago (N-B)
IvyPanda. (2020, May 22). Healthy Lifestyle and Eating. https://ivypanda.com/essays/healthy-lifestyle-and-eating/
"Healthy Lifestyle and Eating." IvyPanda , 22 May 2020, ivypanda.com/essays/healthy-lifestyle-and-eating/.
IvyPanda . (2020) 'Healthy Lifestyle and Eating'. 22 May.
IvyPanda . 2020. "Healthy Lifestyle and Eating." May 22, 2020. https://ivypanda.com/essays/healthy-lifestyle-and-eating/.
1. IvyPanda . "Healthy Lifestyle and Eating." May 22, 2020. https://ivypanda.com/essays/healthy-lifestyle-and-eating/.
Bibliography
IvyPanda . "Healthy Lifestyle and Eating." May 22, 2020. https://ivypanda.com/essays/healthy-lifestyle-and-eating/.
What Really Happens to Your Body When You Exercise and Eat Healthy

What Really Happens to Your Body When examines the head-to-toe effects of common behaviors, actions and habits in your everyday life.
You probably don't need anyone to tell you that diet and exercise are good for you. It's pretty much the same advice that's been given since the days of ancient Greece.
Advertisement
The benefits of how a nutritious diet and exercise can benefit all of you — body and mind — get lost in diet culture, where the focus is far too often is simply on weight. Here's what happens to your body when you start pairing good nutrition with exercise (hint: it's all good!).
Video of the Day
Your Heart Health Will Improve
One of the first signs that your heart may be in danger is developing high blood pressure — and that's something you want to stop in its tracks when you see it creeping up. Why? The strain from high blood pressure can lead to atherosclerosis, which can cause a heart attack, per the American Heart Association (AHA).
The AHA calls high blood pressure the "silent killer" because it often goes undetected for long periods of time before it's caught. Normal blood pressure is under 120/80mm Hg for adults, so get yours checked to see where your numbers are.
So, how do diet and exercise help? Some folks with high blood pressure have a genetic predisposition to it, but that doesn't mean you can't do anything about it. Diet plays an important role in preventing and treating high blood pressure. A diet high in processed foods is often high in sodium and that excess sodium may be partly responsible for raising your blood pressure.
You can do a couple of things to get rid of this risk factor. The first: Change your diet. The DASH (Dietary Approaches to Stop Hypertension) diet is a specialized eating plan that cuts your sodium back to no more than 2,300 milligrams per day, according to the National Institutes of Health . It focuses on fruits, vegetables, lean proteins, whole grains, and low-fat dairy. This large amount of fruits and vegetables isn't just about getting you to eat your broccoli, it actually has a clinical significance.
You see, most fruits and vegetables are sources of potassium. Potassium helps your body release sodium and can help ease the tension in your blood vessels, according to the AHA. This naturally helps lower your blood pressure .
Exercise also helps to take that blood pressure down by naturally releasing nitric oxide. Nitric oxide is known as a vasodilator, which means it opens up your blood vessels, helping blood to flow more freely and this helps lower your blood pressure, according to Harvard Health Publishing.
Your Blood Sugar Might Drop
If you have high blood sugar, or pre-diabetes, you have probably been told that exercise is good for blood sugar control. That's absolutely true. The American Diabetes Association states that exercise can help lower your blood sugar for 24 hours or more after exercise by making your body more sensitive to insulin.
So, how does this work exactly? When you exercise, whether you have high blood sugar or not, you have transporter proteins in your body called GLUT4. These glucose transporters help move glucose out of the blood and into the cells to be used for energy. Increasing GLUT4 in the body can help improve, and in some cases even reverse, type 2 diabetes, per a May 2022 StatPearls report.
Let's not forget about the role of diet in keeping blood sugar under control. A diet rich in fruits, vegetables, lean proteins, dairy and whole grains can give you enough fiber and protein to help keep blood sugar spikes at bay. The Academy of Nutrition and Dietetics recommends getting 14 grams of fiber per every 1,000 calories you eat per day.
Foods high in fiber and/or protein are digested and absorbed slower, which helps to regulate blood sugar levels, according to the Academy of Nutrition and Dietetics.
You Might Lose Weight
Obviously, one reason to get out there and hit the pavement and eat nutritiously is to maintain a healthy weight and prevent or overcome obesity. According to the Centers for Disease Control and Prevention (CDC), some of the health consequences of obesity include:
- High blood pressure
- Heart disease
- Type 2 diabetes
- Osteoarthritis
- Gallbladder disease
- Sleep apnea
- Low quality of life
Losing weight won't solve all of your problems, but it might keep you from developing one or more of these conditions if you have overweight or obesity. The key to preventing many of these conditions is diet and exercise.
You may hear that one or the other — diet or exercise— will independently help you lose weight. In some cases, this may work, but the results are even more pronounced and accelerated when done together.
Your Gut Health Will Improve
You are the host to a vast array of microorganisms in your gut working hard to keep you healthy. That world inside your gut is known as the microbiome, and what you eat has a lot to do with the health of your gut.
The Western diet — which is characterized by a diet high in added sugars, saturated fats and sodium — is disruptive of the healthy balance of bacteria in the gut, which can leave you susceptible to illness, according to a study published in the journal Nutrients in August of 2019.
Changing the way you eat — and focusing on the amount of fiber you eat in a day — could help restore the balance in your gut.
Now, what's really interesting is that exercise seems to do the same thing for the gut. Exercise helps reduce inflammation in the gut and promotes greater bacteria diversity, both of which promote a healthy microbiome, according to March 2017 research in Oxidative Medicine and Cellular Longevity .
You'll Have More Energy
Feeling sluggish all the time can be the first indicator that something is wrong with your diet. In fact, there are certain elements in your diet that can steal your energy and others that can put the pep back in your step.
Not having enough water in your diet is sure to give you a little fatigue. Water is essential to keep your energy high and a huge part of a nutritious diet, per Harvard Health Publishing . In addition, crash dieting or fad diets that exclude entire food groups may be robbing you of much-needed nutrients, which can zap your energy. Keeping variety in your diet with food from all food groups ensures that you meet nutrient requirements, especially for iron and B vitamins.
Now, when you pair the improvements in your diet with a little daily exercise, you might feel like you can conquer the world (or just get through the workday without feeling tired). Harvard Health Publishing suggests exercise for fatigue because it boosts dopamine, serotonin and norepinephrine in your brain, which all give you energy.
Also, as your body gets stronger from exercise, it becomes more efficient and takes less energy to do smaller tasks, so you won't tire out as easily. That saves energy for that after-dinner stroll.
Your Mental Health Might Look Up
Your mental health is just as important as your physical health, and diet and exercise play more of a role than you might think.
According to a September 2018 study in The Lancet Psychiatry , those who exercised had fewer days of poor mental health than those who did not exercise. The researchers found this association with exercising just three to five times per week with team sports, cycling and going to the gym.
Some of the issues related to poor mental health include inflammation and poor gut health, according to April 2019 review study in Psychosomatic Medicine . Some of the nutrients mentioned in the study with the potential to benefit those pathways in the body include:
- Omega-3 fatty acids : found in fatty fish, walnuts, flaxseeds
- B vitamins : found in whole grains, fruits, vegetables
- Magnesium : found in almonds, seeds, spinach
- Fiber : found in fruits, vegetables, whole grains
- Probiotics : found in yogurt, sauerkraut, kimchi
How to Get Started
So you're ready to start eating more nutritiously and exercising — the health benefits speak for themselves.
Before you start an exercise program, you should always check with your doctor to make sure you can start your preferred exercise program. Then, seek out a personal trainer or certified strength and conditioning specialist to help guide you until you're comfortable enough to take the reins on your own.
If diet is where you need help, ask for a referral for a registered dietitian (RD) who can help evaluate the way you eat and see where you need to make changes. An RD can help you create a meal plan that delivers all the nutrients you need to help you reach your goals.

What Really Happens to Your Body When You Eat Processed Foods

What Really Happens to Your Body When You Start Exercising

What Really Happens to Your Body When You Walk Every Day
- American Heart Association: "How High Blood Pressure Can Lead to a Heart Attack"
- Harvard Medical School: "Exercise and Your Arteries"
- American Diabetes Association: "Blood Glucose and Exercise"
- NCBI: "Physiology, Glucose Transporter Type 4 (GLUT4)"
- Academy of Nutrition and Dietetics: "What is Glycemic Index?"
- Harvard Medical School: "Eating to Boost Energy"
- The Lancet Psychiatry: "Association between Physical Exercise and Mental Health in 1·2 Million Individuals in the USA Between 2011 and 2015: A Cross-Sectional Study"
- Harvard Medical School: "Refueling Your Energy Levels"
- Academy of Nutrition and Dietetics: "Fiber"
- Oxidative Medicine and Cellular Longevity: "Exercise Modifies the Gut Microbiota with Positive Health Effects"
- National Institutes of Health: "DASH Eating Plan"
- Psychosomatic Medicine: "The Effects of Dietary Improvement on Symptoms of Depression and Anxiety: A Meta-Analysis of Randomized Controlled Trials"
- Nutrients: "Diet and Immune Function"
An official website of the United States government
Here’s how you know
Official websites use .gov A .gov website belongs to an official government organization in the United States.
Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you’ve safely connected to the .gov website. Share sensitive information only on official, secure websites.
- Entire Site
- Research & Funding
- Health Information
- About NIDDK
- Weight Management
- Healthy Eating & Physical Activity for Life
- Español
Healthy Eating & Physical Activity for Life
Consuming healthy foods and beverages, along with getting regular physical exercise, may help you reach and maintain a weight that suits you. Maintaining that weight, getting adequate sleep, and managing stress may also help prevent some health problems.
This series offers tips for developing and maintaining healthy habits at various life stages, including adulthood, pregnancy, parenthood, and later in life.
Start taking steps now to move more and eat better—for yourself and your loved ones!

Health Tips for Adults
A balanced eating plan, regular physical activity, and stress relief may help you reach and maintain a weight that suits you. Calculate your body mass index (BMI), a measure of healthy body weight. Learn the key daily decisions that may help both men and women improve health.
Helping Your Child: Tips for Parents
Share a few tips with your children on how to eat and drink enough to fuel their bodies and get them moving. Work together as a family to form healthy habits—such as getting adequate sleep and limiting screen time. Learn how to tell if your child is overweight.
Health Tips for Pregnant Women
Whether you’re ready to try for a baby or are already pregnant, you may be inspired to get healthy. Learn what to eat, how to stay active, and how much weight to gain during pregnancy. Good habits now may help you have a healthy pregnancy and a healthy baby.
Health Tips for Older Adults
As you grow older, good nutrition and staying active are as important as ever, but both men and women may need to make a few changes. Plan nutrient-rich meals on a budget. Learn how to stay healthy and engaged as you mature.
Related Topics
- Changing Your Habits for Better Health
- Understanding Adult Overweight & Obesity
- Preventing Type 2 Diabetes
- Some Myths about Nutrition & Physical Activity
Healthy Eating & Physical Activity Resources
- Just Enough for You: About Food Portions
- Choosing a Safe & Successful Weight-loss Program
- Tips to Help You Get Active
- Staying Active at Any Size
Clinical Trials for Diet, Physical Activity, & Weight Management
Learn about clinical research into how diet and physical activity may help manage body weight at different ages. See which studies are open now.
This content is provided as a service of the National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK), part of the National Institutes of Health. NIDDK translates and disseminates research findings to increase knowledge and understanding about health and disease among patients, health professionals, and the public. Content produced by NIDDK is carefully reviewed by NIDDK scientists and other experts.

Essay on Nutrition And Exercise
Students are often asked to write an essay on Nutrition And Exercise in their schools and colleges. And if you’re also looking for the same, we have created 100-word, 250-word, and 500-word essays on the topic.
Let’s take a look…
100 Words Essay on Nutrition And Exercise
Importance of nutrition.
Eating healthy foods gives your body the energy it needs to work well. Imagine your body like a car. Without the right fuel, a car won’t run smoothly. For us, good food is our fuel. Fruits, vegetables, grains, protein, and dairy give us vitamins and energy. Eating a mix of these helps us grow and stay strong.
Benefits of Exercise
Moving and being active is just as important as eating well. When we exercise, our hearts pump faster, which is good for heart health. Playing sports, running, dancing, or even walking helps our muscles and bones get stronger and keeps our bodies fit.
Combining Nutrition and Exercise
Nutrition and exercise work together like a team. When we eat healthy and move enough, our bodies can work their best. This means we can run faster, think clearer, and feel happier. It’s important to balance good food with fun activities to stay healthy.
250 Words Essay on Nutrition And Exercise
Why eating right and moving more are important.
Eating well and staying active are like two peas in a pod; they work best together. When we eat good foods, they give us the energy to run, play, and even think better. Exercise, or moving our bodies, keeps our muscles and bones strong. It’s like when you play a game, you need both a charged controller and a working console to have fun.
The Power of Good Food
Exercise keeps us healthy.
Moving around is not just for athletes; it’s for everyone. Exercise can be anything that gets you moving: walking, dancing, biking, or playing sports. When we move, our hearts beat faster, pumping more blood to our body. This keeps our heart healthy and can make us feel happier because it releases special chemicals in our brain that make us feel good.
Balance is Key
Balancing what we eat with how much we move is like walking a tightrope. Too much food and not enough exercise can lead to weight gain, while too much exercise and not enough food can make us tired and sick. It’s important to find a middle ground where we eat enough to have energy but also move enough to use that energy.
Remember, eating well and exercising are not just about looking a certain way; they’re about feeling great and being able to do all the things you love to do.
500 Words Essay on Nutrition And Exercise
When we talk about staying healthy, two key things come to mind: eating right and exercising. Just like a car needs the correct fuel to run well, our bodies need good food to work and play. Exercise is like the engine that keeps the car moving. Together, they keep our body-machine running smoothly.
Good Food for a Strong Body
Eating right means choosing foods that are good for you. Imagine your plate is a rainbow. Fruits and vegetables of different colors, like red apples and green spinach, give you a mix of vitamins. These help fight off sickness and keep your body strong. Protein from foods like chicken, beans, or nuts helps build muscles. Carbohydrates from bread and rice give you energy to run and play. Lastly, your body needs a bit of fat from foods like avocados or cheese for energy and to help your brain work well.
Exercise for Health and Happiness
Balance is when you have just the right amount of something. Eating too much or too little can be bad for you. The same goes for exercise. Eating a lot of candy and not enough vegetables can make you feel tired and sick. Not moving enough can make your muscles weak. But too much exercise without enough rest can also be bad. It’s like playing with a toy non-stop until it breaks. Your body needs rest to fix itself and get stronger.
Teamwork: Nutrition and Exercise
Nutrition and exercise work together like a team. Good food gives you the energy to move and play. Exercise helps use that energy and makes you hungry for healthy foods. If you eat well but don’t move much, you might not feel your best. If you exercise a lot but eat only junk food, you might not have the energy to play. It’s like trying to ride a bike with flat tires; it just doesn’t work well.
Starting Good Habits Early
Eating right and exercising are like best friends that help you stay healthy and strong. By making smart choices about food and moving your body every day, you can play, learn, and grow better. Remember, your body is a unique machine that needs care, and you’re the driver. You have the power to keep it running smoothly with good nutrition and exercise.
That’s it! I hope the essay helped you.
Happy studying!
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *

Advertisement
The Health Benefits of Exercise and Physical Activity
- Gastroenterology, Critical Care, and Lifestyle Medicine (SA McClave, Section Editor)
- Published: 14 July 2016
- Volume 5 , pages 204–212, ( 2016 )
Cite this article

- Keith R. Miller 1 ,
- Stephen A. McClave 2 ,
- Melina B. Jampolis 3 ,
- Ryan T. Hurt 4 ,
- Kristine Krueger 2 ,
- Sarah Landes 2 &
- Bryan Collier 5
27k Accesses
51 Altmetric
Explore all metrics
Physical inactivity is a modifiable risk factor (similar to dyslipidemia and hypertension) for a variety of chronic diseases, including cancer and cardiovascular disease. Exercise provides a clear health benefit, which serves in the primary and secondary prevention of these disease processes (the most important being a reduction in cardiovascular disease and premature death). The physiologic mechanisms for such a benefit occur at both a cellular and multisystem level. Prolonged periods of occupational or leisure-time sitting have adverse health effects independent of exercise performed before or after. Almost any form of physical activity (PA) is beneficial, whether part of a regular exercise program or as a series of intermittent, incidental, non-purposeful, lifestyle-embedded activity (causing non-exercise activity thermogenesis or NEAT). The health benefits of exercise appear to be dose-dependent. Physicians should recommend near daily exercise which includes at various times strength training, stretching, and aerobic activity in addition to emphasizing adjustments that allow for reduced sitting and increased activity during daily routines. Patients should understand that for optimal health, exercise is no longer optional.
Similar content being viewed by others
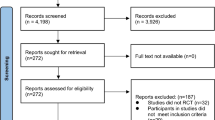
The Best Exercise Modality and Dose to Reduce Glycosylated Hemoglobin in Patients with Type 2 Diabetes: A Systematic Review with Pairwise, Network, and Dose–Response Meta-Analyses
Minimal-Dose Resistance Training for Improving Muscle Mass, Strength, and Function: A Narrative Review of Current Evidence and Practical Considerations
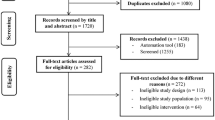
Effects of HIIT Interventions on Cardiorespiratory Fitness and Glycemic Parameters in Adults with Type 1 Diabetes: A Systematic Review and Meta-Analysis
Avoid common mistakes on your manuscript.
Introduction
Physical inactivity is a modifiable risk factor for cardiovascular disease, obesity, depression, cancer, diabetes mellitus, hypertension, and osteoporosis. Physical exercise reduces the risk of premature death and prolongs longevity, and is an important treatment modality in the primary and secondary prevention of the above disorders [ 1 ]. For most states in this country, less than half of the population meets CDC exercise recommendations [ 2 •]. The decline in physical activity (PA) occurs both at work and in leisure time, and may have at least partially contributed to the increase in obesity over the past 30 years. Low recreational physical activities have been associated with a threefold increase for major weight gain in men and a fourfold increase in women [ 3 ]. Surveys of PA across the lifecycle show that physical exercise peaks in the middle high-school age range and begins declining through high school and into adult life. A vicious cycle of decline occurs between inactivity and loss of skeletal muscle mass which accelerates with age. With avoidance of activity requiring effort, there is increased loss of exercise capacity. This loss causes the perception of effort associated with even sub-maximal work to worsen, as the anaerobic threshold decreases. The vicious cycle contributes to further inactivity and deterioration of physical function. The only treatment that can break the cycle is exercise.
Impact of Exercise on Aging
Exercise provides powerful health benefits for quality of life, physical function, and independent living throughout the life cycle. Exercise impedes the aging process and promotes longevity. Observational studies have shown that even in the presence of disease processes such as hypertension (HTN), chronic obstructive pulmonary disease (COPD), diabetes, smoking, high body mass index (BMI), and hypercholesterolemia, increasing PA has a dose-dependent effect in decreasing relative risk of death [ 4 ]. In a study of subjects over a 13-year time period, both baseline fitness, and improvement in physical fitness through exercise and PA was associated with significant increases in longevity [ 4 ]. Functional independence with advanced age relates to the overall level of physical fitness. Physical fitness is most affected by the status of the cardiorespiratory and vascular systems, as well as muscle function [ 5 •].
Garatachea et al. provide an excellent review of the effect of exercise on the physiologic changes associated with aging [ 5 •]. Exercise exerts its positive influence on both a cellular level and at the level of organ systems. At the cellular level, exercise helps reduce genomic instability, epigenetic alteration, loss of proteostasis, dysregulated nutrient sensing, cellular senescence, and altered intracellular communication that leads to inflammation. These effects alter the way the body performs transcellular signaling in the skeletal muscle, the turning on and off of genes through epigenetics, and the manner in which the system manages reactive oxygen species [ 5 •]. On a multisystem level, the benefits of exercise include improvement in brain, cardiovascular, lung, and muscle function, favorable alterations in body composition, and advantageous changes in metabolic responses. The report concludes by suggesting that in the future, pharmaceuticals should be designed which mimic the effects of exercise on the aging process [ 5 •].
Effect of Exercise on Treatment of Disease
Robert Butler from the National Institute on Aging has said that “If exercise could be put in a bottle, it would be the strongest medicine money could buy” [ 6 ]. Exercise helps prevent common chronic diseases (primary prevention), and often plays an important role in the treatment of these disease processes (secondary prevention). Specific benefits from exercise have been seen with cardiovascular disease, stroke, diabetes mellitus, depression, cancer, obesity, and osteoporosis [ 7 , 8 ]
Cardiovascular Disease
Increased levels of PA and physical fitness have a graded effect in reducing the risk of death from cardiovascular disease. The relative risk from all cause and cardiovascular disease mortality is reduced 20–35 % by exercise and PA [ 9 ]. In an observational study, subjects in the lowest quintile of exercise had a relative risk of 3.4 in men and 4.7 in women for death compared to those in the highest quintile [ 10 ]. An increase in activity-related energy expenditure by as little as 1000 kcal or 1 metabolic equivalent (MET)-hour of exercise per week has a mortality benefit of 20 % [ 11 ]. Physically inactive women have a 52 % increase in death, a cardiovascular disease-related death that is doubled, and a cancer-related death rate that is increased by 29 % [ 11 ]. These risks on mortality from inactivity are similar to other modifiable risk factors such as HTN, hypercholesterolemia, and obesity. In randomized controlled trials (RCT)s, exercise and PA are valuable for the secondary prevention of cardiovascular disease. Whereas in the past, traditional recommendations for patients with a heart attack included rest and physical inactivity. Newer information demonstrates that exercise actually attenuates or reverses risk of cardiovascular disease [ 12 ]. The benefit of exercise is seen in cardiac rehabilitation, where increasing PA reduces the risk of premature death following a myocardial infarction [ 12 ]. Added energy expenditure of 1600 kcal/week from exercise may halt the progression of heart disease and energy expenditure of >2200 kcal/week can lead to plaque reduction [ 13 ]. The minimum training recommendation for patients following myocardial infarction is to reach 45 % of their heart rate reserve through cardiac rehabilitation [ 12 , 13 ].
Multiple mechanisms have been identified whereby exercise reduces the risk of premature death [ 4 ]. Exercise affects body composition by decreasing abdominal adiposity and improving weight control. Exercise enhances lipid profiles by reducing serum triglyceride levels, raising HDL, and reducing the LDL/HDL ratio. In addition, a recent meta-analysis showed beneficial changes in lipoprotein subclasses associated with regular exercise including a reduction in small LDL-p and an increase in large LDL-p [ 14 ]. Exercise enhances hemodynamics by decreasing blood pressure, increasing cardiac function, and improving coronary blood flow. Autonomic tone is enhanced and shear stress-mediated endothelial function is improved. Exercise reduces systemic inflammation, as evidenced by reduced C-reactive protein (CRP) levels. Improved psychological well-being in response to exercise is associated with reduced stress, anxiety, and depression [ 4 ].
PA is inversely correlated with risk of incident stroke as shown in a large nurses’ health study [ 15 ]. Habitual exercise reduces risk of stroke by 40–50 % at the highest level of PA. Change in PA is protective against stroke as evidenced by the fact that an increase of 3.5 h of exercise or PA per week is associated with a 29 % reduction in ischemic stroke [ 15 ].
Diabetes Mellitus
Exercise is valuable in both the primary and secondary prevention of diabetes mellitus. Aerobic and resistant-type exercise reduces the likelihood of developing type-2 diabetes mellitus. For each 500 kcal of energy expended per week, there is an associated 6 % reduction in the likelihood of type-2 diabetes (which may be even greater with increasing BMI) [ 16 ]. In patients already diagnosed to have diabetes mellitus, walking 2 h per week is associated with a 39–54 % reduction in all-cause mortality from diabetes mellitus, and a 34–53 % reduction in mortality related to cardiovascular disease [ 17 ]. The benefit of exercise on glycemic control appears to be greater with resistance training than aerobic exercise. A meta-analysis of exercise and PA in diabetes showed that exercise reduces hemoglobin A1C by 0.66 %, an effect similar to intensive glucose-lowering pharmacologic therapy [ 18 ]. The mechanisms by which exercise benefits diabetes relate to the fact that exercise increases glycogen synthetase and hexokinase activity [ 4 ]. Exercise reduces GLUT-4 protein and messenger RNA expression and increases muscle capillary density, which helps improve glucose delivery to the muscle [ 4 ].
Increasing PA, either occupational or at leisure, has been shown to exert a primary preventative effect on two cancers—breast and colon cancer [ 19 ]. Moderate exercise of as little as 4–5 METs (equivalent to mowing the lawn or brisk walking), is required to achieve this effect [ 20 ]. Exercise is associated with a 20–30 % reduction in the incidence of breast cancer in women, and a 30–40 % reduction in the incidence of colon cancer in both men and women [ 20 ]. In those patients already diagnosed to have one of these cancers, exercise reduces the likelihood for cancer recurrence and reduces risk from cancer death by as much as 26–40 % [ 21 ]. PA improves quality of life and overall health status in cancer patients. The mechanisms by which exercise improves risk from cancer may relate to reduced fat stores, an increase in energy expenditure offsetting a high-fat diet, activity-related changes in sex hormone levels, improvement in immune function, and reduced generation of free oxygen radicals [ 4 ].
Osteoporosis
Exercise has a valuable effect in the primary prevention of osteoporosis. Routine PA minimizes age-related bone loss. Weight-bearing exercise (especially resistance exercise) increases bone density compared to low impact non-weight-bearing exercise. Exercise prevents 1 % of bone loss per year, an effect which is greater in post-menopausal than pre-menopausal women [ 22 ]. In RCTs, exercise reduces the risk and number of falls, as well as the risk of fracture [ 22 ]. Even in men, PA reduces the risk of fracture by 62 % over the age of 21 years [ 23 ]. Exercise is also valuable in the secondary prevention of osteoporosis. RCTs in the past have shown that exercise with resistance training increases bone density in older osteoporotic women by as much as 1.4 %, while agility training alone increases bone density by 0.5 % [ 24 ]. Stretching, which was used as sham control, was shown to have no effect on the expected decrease in bone density with age [ 24 ]. In a 12-year follow up of over 60,000 post-menopausal women, risk of hip fracture was lowered 6 % for each increase of three MET-hours per week of activity (the equivalent of walking three miles in 1 h) [ 25 ]. Active women with at least 24 met-hours of exercise per week had a 55 % lower risk of hip fracture than sedentary women with no other exercise. Walking at least 4 h per week was associated with a 41 % lower risk of hip fracture than walking less than one hour per week [ 25 ].
Exercise has a valuable therapeutic effect on the treatment on multiple types of depression, including dysthymic, seasonal, bipolar, post-natal, pre-menstrual, atypical, and major depression [ 26 ]. The value in treating depression comes from an innate anti-depressive effect from exercise. Combining exercise with psychotropic medications achieves better treatment results than the same medications alone [ 26 ]. Exercise is relatively inexpensive, safe, and has minimal side effects when done correctly. Exercise may help reduce the dose of anti-depressive medications required. Subjects are less likely to relapse with an active exercise program [ 26 ].
The patients with depression who are most likely to benefit from exercise include those with age <20 or >40 years, higher education, higher baseline physical status, females, untrained subjects, and those with mild to moderate depression [ 26 ]. There are a number of aspects of exercise that get the optimal results in treating depression including programs that are structured, individually tailored to the patient, low to moderate intensity, when it is used as an adjunct to medication therapy, and exercise that is a combination of aerobic or resistive training performed 3–4 times per week [ 26 ]. The mechanism of effect from exercise on depression occurs on a systemic level as well as a direct effect on central nervous system (CNS) function. Exercise appears to increase serotonin, ACTH, endorphins, and endocannabinoids within the CNS. On a systemic level, exercise increases norepinephrine and reduces cortisol, tumor necrosis factor (TNF), and interleukin-6 [ 26 ].
In a controversial article that appeared in Time magazine in 2009, the journalist John Cloud wrote about “The Myth of Exercise” and its effect on treating obesity [ 27 ]. The article suggested that exercise was not good for weight management in obesity. The author pointed out that exercise leads to increased appetite and intake of food and causes a decrease in non-exercise energy expenditure, and therefore that exercise was a poor strategy for weight loss [ 27 ]. A number of letters to the editor of Time magazine followed the publication of this article, including letters from the American Society for Sports Medicine, arguing that facts were misrepresented and that the article gave the wrong message about the health benefits of exercise.
A recent review by Swift clarified the role of exercise in managing or preventing obesity, and suggested that Cloud’s article was in fact an accurate portrayal of the facts [ 28 ]. The key issue of Swift’s review is that exercise without caloric restriction is unlikely to succeed in weight loss [ 28 ]. Increasing PA can prevent weight gain, but it requires 150–250 min per week of moderate to vigorous exercise or 1200–2000 kcal/week expended through exercise to accomplish this feat [ 29 ]. Aerobic exercise by itself is minimally helpful in promoting weight loss, successful in loss of only 0–2 kg total [ 29 ]. Extreme high-volume aerobic exercise can achieve significant weight loss, but this is usually unsustainable by most obese patients. Moderate intensity, surprisingly, is no different than vigorous intensity in achieving weight loss, unless subjects are matched for exercise duration. Resistance training by itself has no impact on weight loss, and aerobic training combined with resistant training has no greater effect than aerobic training alone. However, adding caloric restriction to aerobic training does result in successful weight loss of 9–13 kg, and higher intensity of exercise has the potential for even greater weight loss [ 29 ]. Some obese subjects do experience weight compensation in response to exercise, defined by the circumstances where less weight is lost than expected with the amount of exercise sustained, often a factor related to an increase in caloric intake [ 28 , 30 ]. This is more likely to occur in women performing 150 % of weekly recommendations (compared to women performing only 100 % or 50 % of weekly recommendations) [ 28 , 30 ]. Even if minimal or no weight loss occurs in response to exercise, obese subjects still benefit from the increase in PA due to increased cardiorespiratory fitness, glucose control, endothelial function, improvements in hyperlipidemia, quality of life, and a reduction in future weight gain [ 28 ].
Caloric restriction is better than exercise for significant weight loss initially, and the weight loss is not necessarily enhanced significantly by adding exercise [ 28 ], although exercise training plus caloric restriction does improve body composition by increasing fat loss and decreasing loss of lean body mass [ 31 ]. The greatest value of exercise in the management of obesity occurs not in the initial weight loss, but in the situation where obese patients have lost weight successfully and now require substantial PA to maintain that weight loss [ 28 ]. Interestingly, an “energy gap” has been identified as the difference in energy expenditure before and after weight loss [ 32 ]. The energy gap is estimated to be approximately 8 kcal per day per pound of weight lost. An energy gap, for example, of 40 lbs lost would be associated with 320 kcal of energy. Sustaining this weight loss successfully would require either a continued reduction in energy consumption by 320 kcal per day, or increasing activity-associated energy expenditure by the same amount [ 32 ]. Based on the Set Point theory, both biological and environmental pressures oppose the strategy of food restriction in keeping weight off, but the same effect does not occur with increased PA [ 32 ]. Therefore, while food restriction is the key to weight loss, PA is the key to successful maintenance of the weight lost [ 32 ]. The ACSM has identified that people who successfully maintain weight loss average at least 250 min of PA per week [ 29 ].

Low Back Pain
A 2016 systematic review and meta-analysis reviewed 23 randomized controlled trials evaluating the prevention of low back pain [ 33 ]. Over 30,000 patients were involved in these studies. Ultimately, the combination of exercise (varying regimens of abdominal strengthening, core stability, cardiovascular, and isometrics) plus education regarding prevention of low back pain was found to reduce the risk of low back pain as well as sick leave related to low back pain. Exercise alone was also found to have an impact but had a more short term effect (<12 months), thought to be due to cessation of exercise following the intervention. Other interventions, including back belts, insoles, and education alone were not found to have any impact [ 33 ].
Not All Exercise is Created Equal
Physical activity versus physical fitness.
The lay public tends to use the terms PA and physical fitness interchangeably, but subtle differences between the two exist. Physical fitness is a physiologic state of being with regard to daily living and/or sports performance [ 4 ]. Physical fitness is comprised of cardiovascular, musculoskeletal, body composition, and metabolic components [ 4 ]. Physical fitness is similar to PA, but is more predictive of health outcomes. For example, a high-fit versus a low-fit person is estimated to have a 50 % lower mortality [ 34 ]. Physical fitness, therefore, becomes a better measure of PA than self-reporting. From a public health standpoint, however, it is better and more productive to encourage the public to be physically active and not push the need to be physically fit. Eventually, increased activity should lead to physical fitness.
In the past, guidelines for optimal health seemed to have had a singular focus on aerobic fitness. But a new paradigm shift has occurred with the addition of the concept of musculoskeletal fitness [ 4 ]. In other words, health status can improve due to increased PA in the absence of changes in aerobic fitness. Regular PA can decrease risk factors from chronic disease and disability without changing cardiac output or oxidative potential, especially in the elderly [ 4 ]. The shift has been to focus on the health benefits of musculoskeletal fitness, which may be a critical factor in the functional threshold for dependence with the aging population. Loss of muscular fitness can result in loss of capacity for daily living, and a cycle of decline can ensue [ 4 ]. Improvement in musculoskeletal function can delay the onset of disability, dependence, and chronic disease [ 35 ]. Musculoskeletal fitness is associated with fewer functional limitations and a reduced incidence of cardiovascular disease, diabetes, degenerative joint disease, and coronary artery disease [ 35 ]. Therefore, resistance training that works all the major muscle groups (including legs, hips, back, abdomen, chest, shoulders, and arms) and flexibility exercise, which are necessary to achieve musculoskeletal fitness, are recommended to be done at least twice weekly, to complement aerobic fitness and optimize overall health status.
Adverse Health Risk from Sitting
In an effort to delineate those factors which contribute to the obesity epidemic, researchers are increasingly focused on the adverse health risk from prolonged sitting [ 36 •]. A newly recognized occupational hazard has evolved because of workers needing to sit at a computer screen throughout the workday. Each mean hour of sitting after a total mean of 7 h per day is associated with a 5 % increase in premature death [ 36 •]. More time sitting at work has been shown to correlate with more sitting in leisure time. Prolonged sitting while watching TV at home, for example, has adverse effects on mental health, well-being, and muscle strength. Long sedentary hours have been linked to a twofold increase in diabetes, a twofold increase in cardiovascular disease, a 13 % increase in the incidence of cancer, and a 17 % increase in mortality related to cancer [ 36 •]. It is estimated that the average worker in the USA and England spends 60–70 % of waking hours in a sedentary sitting position. The effect of sitting has been likened to the transmission of a car. Sitting for such a prolonged period is like putting a car in reverse, causing one’s overall health status to go in the wrong direction [ 36 •]. Approximately 20–30 % of the time is spent in light intensity activity, described as postural changes, standing and movement, or ambulation. For less than 5–10 % of waking hours, individuals spend in moderate to vigorous PA. The adverse effect of sitting on health status is independent of the exercise or PA done before or after [ 36 •]. In other words, no amount of PA later can overcome the negative health effects of prolonged sitting.
Changes in the workplace environment may be the key issue to minimizing the negative effects of prolonged sitting. Particularly, in the UK, recommendations and guidelines have been developed to avoid this health hazard [ 36 •]. Workers are encouraged to accumulate up to 2 h per day at work standing or performing light walking, with the goal to progress ultimately to 4 h per day. Workers should interrupt seat-based work with standing-based work. However, workers should avoid both prolonged periods of standing as well as prolonged periods of sitting. Adaptation of these guidelines may lead to musculoskeletal complaints and fatigue, which should be monitored by managers in the workplace. Such health promotion strategies should eventually extend from the workplace to the leisure time [ 36 •].
Non-Exercise Activity Thermogenesis
Non-exercise activity thermogenesis (NEAT) has been described as unstructured PA, energy expended unrelated to sleeping, eating, or sports exercise. NEAT is energy expended outside of purposeful exercise [ 37 ]. Surprisingly, this incidental, non-purposeful lifestyle-embedded PA can have tremendous health benefits. Three components of NEAT include body posture, ambulation, and all other movements (the most important of which may be fidgeting) [ 38 ]. Researchers involved in the study of obesity are finding that in some cases what delineates the lean subject from an obese one is a difference in NEAT, not exercise-associated activity thermogenesis [ 38 ]. Early experiments which helped identify NEAT came from studies where energy requirements were measured and all subjects were placed on a diet of 1000 cal over requirements [ 39 ]. Subjects were then videotaped, and in a blinded fashion designated as fidgeters or non-fidgeters. At the end of the trial, those patients who were designated as fidgeters failed to gain weight, while those identified to be non-fidgeters sustained significant weight gain. The increase in kilocalories of energy expenditure attributed to NEAT was inversely proportional to fat gain in pounds [ 39 ]. NEAT ranges from 15 % of total energy expenditure (TEE) in sedentary subjects to as much as 50 % of TEE in fidgeting physically active people [ 39 ]. Fidgeting has been shown in twin studies to be genetic, with an estimated >62 % heritability [ 40 ]. Simply standing or lightly ambulating can increase energy expenditure by an average of 350 kcal/day (range 269–477 kcal/day) [ 37 ]. NEAT tends to be greater in men than women, in obese subjects rather than lean, and in those with more education than those with less [ 38 , 39 ]. NEAT tends to be seasonal and overall, declines with age [ 39 ]. The concept of an energy gap is pertinent to NEAT. An average citizen in the USA has been shown to gain 1–2 lbs each year through their adult life. An energy gap of 100 kcal additional energy consumed each day would account for this weight gain [ 41 ]. NEAT can be an important contributor to TEE, such that increases in NEAT of as little as 100–150 kcal of activity per day could prevent such weight gain (by offsetting the energy gap) in the vast majority of people [ 41 ]. Recommendations now suggest that if you were not lucky enough to inherit fidgeting, you should “act like a fidgeter,” standing often, getting up from sitting, pacing, parking at the back of a parking lot, and taking stairs instead of elevators [ 40 ].
Continuous Versus Interval Exercise
Long bouts of continuous exercise as a strategy for weight loss or weight maintenance can be a contentious and challenging recommendation for the general public. Longer duration, continuous exercise may be difficult and not particularly enjoyable for patients and may not fit as well with work or home schedules. Research now has shown that interval exercise, which involves alternating short bouts of high-intensity exercise with lower-intensity exercise that allows for partial recovery, can match the health benefits of continuous exercise [ 42 ]. Studies in patients with class-1 obesity (BMI 30–34.9 kg/m 2 ), walking at a moderate level of intensity, randomized to two 15-min intervals of walking versus one 30-min interval, showed essentially the same improvements in overall health status [ 42 ]. Both intermittent and continuous exercise resulted in improvement of maximum oxygen consumption, body composition, and lipid profiles. In some categories, interval exercise even exceeded the benefit seen with continuous exercise (such as VLDL levels and percent fat lost) [ 42 ]. The value of these findings for intermittent exercise stems from three factors: there is less attrition with recommendations for interval exercise, time constraints, and short periods of interval exercising may allow for greater intensity of PA [ 42 ]. An additional study involving 28 sedentary overweight or obese men compared five 45- to 60-min sessions of continuous moderate intensity cycling per week for 6 weeks with three 20-min sessions of high-intensity interval exercise per week (for a total of 60 min) for 6 weeks. Similar improvements in cardio-metabolic risk factors including improved insulin sensitivity, cardiovascular fitness, and a reduction in blood lipids and body fat percentage were observed in the groups [ 43 ]. While cardiovascular fitness was improved to a greater extent in the continuous exercise group, this study, along with numerous other studies of interval exercise showing similar outcomes in different populations, are encouraging in that they show many of the same improvements in overall health with a substantially reduced time commitment [ 43 ]. This is especially relevant as lack of time is cited as the most common reason for not exercising by many. In addition, interval exercise can be easily adapted to an individual’s starting fitness level by adjusting either the duration or intensity (or both) of the high-intensity component of exercise. This may be especially beneficial for sedentary overweight or obese individuals who are new to exercise. In light of both the potential health and time saving benefits, interval exercise training appears to be an appealing and worthwhile exercise option in addition to, or instead of, continuous exercise. The good news for public health is that short walks on a subject’s lunch break or brief periods of activity before and after work all count, and the sum of their duration may have similar benefits to a single continuous interval of exercise of the same duration.
Success of Pedometers
The use of pedometers to increase PA was generated years ago in Japanese walking clubs. The rationalization for the pedometer was that the average stride was estimated to be 2.5 ft. Therefore, 2000 steps should approximately equal a mile, 10,000 equaling about 5 miles [ 44 ]. Based on this rationalization, PA can be classified as sedentary (<5000 steps per day), low active (5000 to 7500 steps), somewhat active (7500 to 10,000 steps), and active (>10,000 steps per day). Highly active physical exercise is associated with >12,500 steps per day [ 44 ]. This is an arbitrary categorization, however, and 10,000 steps per day may be too little for children or too much for the elderly. Weight loss using a pedometer without caloric restriction is associated with minimal to modest weight loss of <2 kg [ 44 ]. Health benefits associated with use of the pedometer may be limited to a reduction in blood pressure, with not much change in cholesterol, triglycerides, or fasting glucose [ 44 ].
Exercise in the Intensive Care Unit
Exercise is becoming increasingly important in one of the least expected circumstances, that of a critically ill patient in the intensive care unit (ICU). Researchers have found that exercising muscle increases the uptake of amino acid fuel and promotes greater protein synthesis [ 45 , 46 ]. Patients in the ICU on a ventilator in some centers are gotten out of bed and encouraged to walk with assistance in the hallway. Other centers have used a pedaling device, some of which can even be adapted for passive activity in a patient who is otherwise sedated and minimally responsive. Exercise in the critical care setting helps maintain muscular strength, reduces the risk for long-term neuromuscular weakness, shortens rehabilitation, and is more likely to result in the patient being discharged to their home [ 45 , 46 ].
Recommendations for Public Health
Similar to the Food Guide Pyramid designed by the USDA, an activity pyramid has been created to guide the public in strategies to increase flexibility, muscular strength, and aerobic capacity ( www.wellspan.org/media/3648/activitypyramid-2009.pdf ). Every day, subjects are encouraged to increase activity in leisure and at work. Three to five times per week, aerobic activity should occur, accumulating 150 min each week ( www.wellspan.org/media/3648/activitypyramid-2009.pdf ). Two to three times per week, muscular activity focusing on flexibility and strength training should be scheduled. Sitting more than 30 min at a time, watching TV, or staring at a computer screen should be minimized or reduced as much as possible ( www.wellspan.org/media/3648/activitypyramid-2009.pdf ).
Guidelines differentiate between moderate and vigorous intensity of PA. Moderate intensity is defined by a 3–5 MET level of effort, and includes activities that cause some increase in breathing and heart rate (such as walking 3–4 miles per hour, bicycling on level ground, light swimming, gardening, or mowing a lawn) [ 4 ]. Vigorous intensity is defined by ≥6 METs, and is exemplified by activities causing large increases in breathing, heart rate, and sweating. Such activities of vigorous intensity would include jogging or running at faster than a 10 min mile, aerobic dancing, competitive sports, heavy yard or construction work, brisk swimming, or fast bicycling [ 4 ].
The amount of PA needed to optimize health is not clear. The particular dose of exercise required to achieve benefits with regard to a particular disease process is difficult to ascertain. For cardiovascular disease, the intensity of PA is inversely and linearly associated with increased mortality, with the biggest effect seen as a reduction of premature death [ 47 ]. PA of >2000 kcal per week extends life by 1–2 years by age 80 [ 47 ]. An average energy expenditure of 1000 kcal per week is associated with a 20–30 % decrease in all-cause mortality. Beginning at a minimum of 1000 kcal per week, increasing benefits are seen with increasing energy expenditure, suggesting a dose-response gradient to the effect of exercise on cardiovascular health [ 47 ]. For diabetes mellitus, there is decreased risk from this disease process with PA of >5.5 METs for at least 40 min per week [ 48 ]. Walking 2 h per week decreases the risk of premature death from diabetes [ 48 ]. Moderate exercise defined by a >4.5 METs for 30–60 min per day reduces both the risk of colon cancer and breast cancer [ 19 ]. For women in particular, >7 h per week of moderate exercise has been shown to be successful in reducing risk of breast cancer (TI01). For osteoporosis, the dose-response gradient is less clear, with recommendations simply emphasizing that osteogenic adaptation is load-dependent and site-specific [ 4 ]. The Center for Disease Control (CDC), the American College of Sports Medicine, and the Healthy People 2010 recommendations provide guidelines for aerobic activity for public health purposes [ 49 ]. Adults should engage in PA of moderate intensity for at least 150 min per week or engage in PA of vigorous intensity for at least 75 min per week. Bouts of exercise may be broken up into smaller increments lasting at least 10 min [ 49 ].
Should Anyone Not be Exercising?
Jim Fixx was a celebrity journalist who helped contribute to the running craze seen in the 1980s in the USA. His sudden death from cardiovascular disease, while jogging, raised questions as to the need for medical evaluation prior to engaging in a program of increasing PA. Moderately strenuous PA may trigger ischemic events, particularly among sedentary people. There is an increased incidence of primary heart attack in high-intensity exercise. In competitive athletes, 80 % of deaths are caused by coronary artery disease. Some subjects do need to have their health risks assessed prior to engaging in an aggressive program.
The degree to which a person is evaluated prior to exercise depends on the presence or absence of cardiovascular disease risk factors and whether the exercise will be moderate or vigorous in intensity [ 50 ]. Subjects at low risk would be those who are young in age (<45 years for male, <55 years for female), are asymptomatic, and have ≤1 cardiovascular risk disease factors. These patients do not need a medical evaluation or stress test for moderate or even vigorous exercise. Subjects at moderate risk are older (men >45 years, women >55 years), or have ≥2 risk factors for cardiovascular disease. For moderate exercise, no medical evaluation may be needed, but these subjects should undergo a stress test. If exercise of vigorous intensity is planned, both a medical evaluation and a stress test should be performed. For those patients at high risk, however, defined by ≥1 sign or symptom of cardiovascular, pulmonary, or metabolic disease, both a full medical evaluation and stress test should be performed before any program is undertaken [ 50 ].
Specifically, those subjects who should not be exercising are those experiencing an acute myocardial infarction, subjects with unstable angina, systolic blood pressure >180, diastolic pressure >110 ml/Hg, uncontrolled diabetes mellitus, poorly controlled congestive heart failure, or thrombophlebitis [ 50 ].
While formal studies have shown that physician counseling is time-intensive and only minimally effective in changing behavior, physicians should no longer avoid the subject of recommendations for exercise as part of the healthcare they deliver to their patients. Physicians can begin by suggesting lifestyle changes such as climbing stairs at work, parking further away from the door on errands, walking regularly, and doing chores at home and in the yard. Clinicians should write on a prescription pad for the patient, specifying the type of exercise, duration, frequency, and intensity. The physician upon discharge from an office visit should determine plans for support and follow up to encourage success, manage obstacles, and prevent relapses. Clinicians should encourage their outpatients to involve community services such as physical therapy, mall-walking programs, school tracks, safe neighborhoods, the YMCA, and walk-a-thon’s.
Physicians should counsel that exercise is not an option. The exercise does not have to be continuous to be effective, and any physical activity counts. Patients should sit less, stand more, and plan their exercise activity at the beginning of each week. Subjects should be encouraged to find activities which they enjoy and involve others to maintain compliance. As Edward Stanley, the Earl of Derby in 1873 said, “Those who think they have not time for bodily exercise will sooner or later have to find time for illness” [ 51 ].
Papers of particular interest, published recently, have been highlighted as: • Of importance
Rezende LF, Rey Lopez JP, Matsudo VK, Luiz OD. Sedentary behavior and health outcomes among older adults: a systematic review. BMC Public Health. 2014;14(1):333.
Article PubMed PubMed Central Google Scholar
www.cdc.gov/nchs/fastats/exercise.htm . Accessed June 12, 2016. Center for Disease Control and Prevention statistics regarding current levels of PA in the United States and trends in physican recommendations to patients relevant to exercise.
Lee IM, Djoussé L, Sesso HD, Wang L, Buring JE. Physical activity and weight gain prevention. JAMA. 2010;303(12):1173–9.
Article CAS PubMed PubMed Central Google Scholar
Warburton DE, Nicol CW, Bredin SS. Health benefits of physical activity: the evidence. CMAJ. 2006;174(6):801–9.
Garatachea N, Pareja-Galeano H, Sanchis-Gomar F, Santos-Lozano A, Fiuza-Luces C, Morán M, et al. Exercise attenuates the major hallmarks of aging. Rejuvenation Res. 2015;18(1):57–89. Discussion regarding the exercise mediated attenuation of physical fitness and functional decline in aging.
"Working With Special Populations Sport Essay." UKessays.com. 11 2013. All Answers Ltd. 06 2016 < https://www.ukessays.com/essays/sports/working-with-special-populations-sport-essay.php?cref=1 >
Blumenthal JA, Babyak MA, Moore KA, Craighead WE, Herman S, Khatri P, et al. Effects of exercise training on older patients with major depression. Arch Intern Med. 1999;159(19):2349–56.
Article CAS PubMed Google Scholar
Byrne A, Byrne DG. The effect of exercise on depression, anxiety and other mood states: a review. J Psychosom Res. 1993;37(6):565–74.
Macera CA, Hootman JM, Sniezek JE. Major public health benefits of physical activity. Arthritis Rheum. 2003;49(1):122–8.
Article PubMed Google Scholar
Blair SN, Kohl 3rd HW, Paffenbarger Jr RS, Clark DG, Cooper KH, Gibbons LW. Physical fitness and all-cause mortality. A prospective study of healthy men and women. JAMA. 1989;262(17):2395–401.
Hu FB, Willett WC, Li T, Stampfer MJ, Colditz GA, Manson JE. Adiposity as compared with physical activity in predicting mortality among women. N Engl J Med. 2004;351(26):2694–703.
Taylor RS, Brown A, Ebrahim S, Jolliffe J, Noorani H, Rees K, et al. Exercise-based rehabilitation for patients with coronary heart disease: systematic review and meta-analysis of randomized controlled trials. Am J Med. 2004;116(10):682–92.
Hambrecht R, Niebauer J, Marburger C, Grunze M, Kälberer B, Hauer K, et al. Various intensities of leisure time physical activity in patients with coronary artery disease: effects on cardiorespiratory fitness and progression of coronary atherosclerotic lesions. J Am Coll Cardiol. 1993;22(2):468–77.
Sarzynski MA1, Burton J2, Rankinen T2, Blair SN3, Church TS2, Després JP4, et al. The effects of exercise on the lipoprotein subclass profile: a meta-analysis of 10 interventions. Atherosclerosis. 2015;243(2):364–72.
Hu FB, Stampfer MJ, Colditz GA, Ascherio A, Rexrode KM, Willett WC, et al. Physical activity and risk of stroke in women. JAMA. 2000;283(22):2961–7.
Helmrich SP, Ragland DR, Leung RW, Paffenbarger Jr RS. Physical activity and reduced occurrence of non-insulin-dependent diabetes mellitus. N Engl J Med. 1991;325(3):147–52.
Gregg EW, Gerzoff RB, Caspersen CJ, Williamson DF, Narayan KM. Relationship of walking to mortality among US adults with diabetes. Arch Intern Med. 2003;163(12):1440–7.
Boulé NG, Haddad E, Kenny GP, Wells GA, Sigal RJ. Effects of exercise on glycemic control and body mass in type 2 diabetes mellitus: a meta-analysis of controlled clinical trials. JAMA. 2001;286(10):1218–27.
Thune I, Furberg AS. Physical activity and cancer risk: dose-response and cancer, all sites and site-specific. Med Sci Sports Exerc. 2001;33(6 Suppl):S530–50. discussion S609-10.
Lee IM. Physical activity and cancer prevention—data from epidemiologic studies. Med Sci Sports Exerc. 2003;35(11):1823–7.
Holmes MD, Chen WY, Feskanich D, Kroenke CH, Colditz GA. Physical activity and survival after breast cancer diagnosis. JAMA. 2005;293(20):2479–86.
Wolff I, van Croonenborg JJ, Kemper HC, Kostense PJ, Twisk JW. The effect of exercise training programs on bone mass: a meta-analysis of published controlled trials in pre- and postmenopausal women. Osteoporos Int. 1999;9(1):1–12.
Kujala UM, Kaprio J, Kannus P, Sarna S, Koskenvuo M. Physical activity and osteoporotic hip fracture risk in men. Arch Intern Med. 2000;160(5):705–8.
Liu-Ambrose TY, Khan KM, Eng JJ, Heinonen A, McKay HA. Both resistance and agility training increase cortical bone density in 75- to 85-year-old women with low bone mass: a 6-month randomized controlled trial. J Clin Densitom. 2004;7(4):390–8.
Feskanich D, Willett W, Colditz G. Walking and leisure-time activity and risk of hip fracture in postmenopausal women. JAMA. 2002;288(18):2300–6.
Ranjbar E, Memari AH, Hafizi S, Shayestehfar M, Mirfazeli FS. Eshghi MA. J Sports Med. 2015;6(2):e24055.
Google Scholar
Cloud J. Why exercise won’t make you thin. Time. 2009;174(6):49–51.
Swift DL, Johannsen NM, Lavie CJ, Earnest CP, Church TS. The role of exercise and physical activity in weight loss and maintenance. Prog Cardiovasc Dis. 2014;56(4):441–7.
Donnelly JE, Blair SN, Jakicic JM, Manore MM, Rankin JW, Smith BK. American College of Sports Medicine. American College of Sports Medicine Position Stand. Appropriate physical activity intervention strategies for weight loss and prevention of weight regain for adults. Med Sci Sports Exerc. 2009;41(2):459–71.
Church TS, Martin CK, Thompson AM, Earnest CP, Mikus CR, Blair SN. Changes in weight, waist circumference and compensatory responses with different doses of exercise among sedentary, overweight postmenopausal women. PLoS One. 2009;4(2):e4515.
Miller CT, Fraser SF, Levinger I, Straznicky NE, Dixon JB, Reynolds J, et al. The effects of exercise training in addition to energy restriction on functional capacities and body composition in obese adults during weight loss: a systematic review. PLoS One. 2013;8(11):e81692.
Hill JO, Thompson H, Wyatt H. Weight maintenance: what’s missing? J Am Diet Assoc. 2005;105(5 Suppl 1):S63–6.
Steffens D, Maher CG, Pereira LS, Stevens ML, Oliveira VC, Chapple M, et al. Prevention of low back pain: a systematic review and meta-analysis. JAMA Intern Med. 2016;176(2):199–208.
Myers J, Kaykha A, George S, Abella J, Zaheer N, Lear S, et al. Fitness versus physical activity patterns in predicting mortality in men. Am J Med. 2004;117(12):912–8.
Warburton DE, Gledhill N, Quinney A. Musculoskeletal fitness and health. Can J Appl Physiol. 2001;26(2):217–37.
Buckley JP, Hedge A, Yates T, Copeland RJ, Loosemore M, Hamer M, et al. The sedentary office: an expert statement on the growing case for change towards better health and productivity. Br J Sports Med. 2015;49(21):1357–62. Expert consensus on techniques to combat increased periods of sitting and inactivity in the modern workplace.
Tremblay MS, Esliger DW, Tremblay A, Colley R. Incidental movement, lifestyle-embedded activity and sleep: new frontiers in physical activity assessment. Can J Public Health. 2007;98 Suppl 2:S208–17.
PubMed Google Scholar
McManus AM. Physical activity—a neat solution to an impending crisis. J Sports Sci Med. 2007;6(3):368–73.
PubMed PubMed Central Google Scholar
Levine JA. Non-exercise activity thermogenesis (NEAT). Nutr Rev. 2004;62(7 Pt 2):S82–97.
Bouchard C, Tremblay A. Genetic influences on the response of body fat and fat distribution to positive and negative energy balances in human identical twins. J Nutr. 1997;127(5 Suppl):943S–7S.
CAS PubMed Google Scholar
Hill JO, Wyatt HR, Reed GW, Peters JC. Obesity and the environment: where do we go from here? Science. 2003;299(5608):853–5.
Campbell L, Wallman K, Green D. The effects of intermittent exercise on physiological outcomes in an obese population: continuous versus interval walking. J Sports Sci Med. 2010;9(1):24–30.
Fisher G, Brown AW, Bohan Brown MM, Alcorn A, Noles C, Winwood L, et al. High intensity interval- vs moderate intensity-training for improving cardiometabolic health in overweight or obese males: a randomized controlled trial. PLoS One. 2015;10(10):e0138853.
Tudor-Locke C, Bassett Jr DR. How many steps/day are enough? Preliminary pedometer indices for public health. Sports Med. 2004;34(1):1–8.
Morris PE, Goad A, Thompson C, Taylor K, Harry B, Passmore L, et al. Early intensive care unit mobility therapy in the treatment of acute respiratory failure. Crit Care Med. 2008;36(8):2238–43.
Schweickert WD, Pohlman MC, Pohlman AS, Nigos C, Pawlik AJ, Esbrook CL, et al. Early physical and occupational therapy in mechanically ventilated, critically ill patients: a randomised controlled trial. Lancet. 2009;373(9678):1874–82.
Paffenbarger Jr RS, Hyde RT, Wing AL, Hsieh CC. Physical activity, all-cause mortality, and longevity of college alumni. N Engl J Med. 1986;314(10):605–13.
Lynch J, Helmrich SP, Lakka TA, Kaplan GA, Cohen RD, Salonen R, et al. Moderately intense physical activities and high levels of cardiorespiratory fitness reduce the risk of non-insulin-dependent diabetes mellitus in middle-aged men. Arch Intern Med. 1996;156(12):1307–14.
U.S. Department of Health and Human Services. Healthy People 2010: Understanding and improving health. 2nd ed. Washington DC: US Government Printing Office; 2000.
Balady GJ, Weiner DA. Exercise testing for sports and the exercise prescription. Cardiol Clin. 1987;5(2):183–96.
http://www.britannica.com/biography/Edward-Stanley-3rd-earl-of-Derby/article-supplemental-information.htm Accessed June 2016
Download references
Author information
Authors and affiliations.
Department of Surgery, University of Louisville School of Medicine, Louisville, KY, 40202, USA
Keith R. Miller
Department of Medicine, University of Louisville School of Medicine, Louisville, KY, USA
Stephen A. McClave, Kristine Krueger & Sarah Landes
National Board of Physician Nutrition Specialists, Valley Village, CA, 91607, USA
Melina B. Jampolis
Department of Medicine, Mayo Clinic, Rochester, MN, USA
Ryan T. Hurt
Department of Surgery, East Virginia University, Roanoke, VA, USA
Bryan Collier
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Keith R. Miller .
Ethics declarations
Conflict of interest.
Keith R. Miller has received compensation from Nestlé for serving as faculty in its fellowship program, from Abbott for serving on a surgical advisory board, and from Metagenics for serving on an advisory board.
Stephen A. McClave declares that he has no conflict of interest.
Melina B. Jampolis declares that she has no conflict of interest.
Ryan T. Hurt has received compensation from Nestlé Nutrition for service as a consultant.
Kristine Krueger declares that she has no conflict of interest.
Sarah Landes declares that she has no conflict of interest.
Bryan Collier declares that he has no conflict of interest.
Human and Animal Rights and Informed Consent
This article does not contain any studies with human or animal subjects performed by any of the authors.
Additional information
This article is part of the Topical Collection on Gastroenterology, Critical Care, and Lifestyle Medicine
Rights and permissions
Reprints and permissions
About this article
Miller, K.R., McClave, S.A., Jampolis, M.B. et al. The Health Benefits of Exercise and Physical Activity. Curr Nutr Rep 5 , 204–212 (2016). https://doi.org/10.1007/s13668-016-0175-5
Download citation
Published : 14 July 2016
Issue Date : September 2016
DOI : https://doi.org/10.1007/s13668-016-0175-5
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Physical activity
- Energy expenditure
- Non-exercise activity thermogenesis
- Find a journal
- Publish with us
- Track your research

We know what to eat to stay healthy. So why is it so hard to make the right choices?
Associate Professor and Associate Director, Mitchell Institute, Victoria University
Disclosure statement
Nina Van Dyke receives funding from the Victorian Department of Health to conduct a policy evidence brief on healthy eating.
Victoria University provides funding as a member of The Conversation AU.
View all partners
A healthy diet protects us against a number of chronic diseases, including heart disease, diabetes and cancer.
From early childhood, we receive an abundance of information about how we should eat to be healthy and reduce our risk of disease. And most people have a broad understanding of what healthy eating looks like.
But this knowledge doesn’t always result in healthier eating.
In our new research, we set out to learn more about why people eat the way they do – and what prevents them from eating better. Lack of time was a major barrier to cooking and eating healthier foods.
How do you decide what to eat?
We spoke with 17 adults in a regional centre of Victoria. We chose a regional location because less research has been done with people living outside of metropolitan areas and because rates of obesity and other diet-related health issues are higher in such areas in Australia.
Participants included a mix of people, including some who said they were over their “most healthy weight” and some who had previously dieted to lose weight. But all participants were either:
- young women aged 18–24 with no children
- women aged 35–45 with primary school aged children
- men aged 35–50 living with a partner and with pre- or primary-school aged children.
We selected these groups to target ages and life-stages in which shifts in eating behaviours may occur. Previous research has found younger women tend to be particularly concerned about appearance rather than healthy eating, while women with children often shift their focus to providing for their family. Men tend to be less interested in what they eat.
We asked participants about how they decided what food to eat, when, and how much, and what prevented them from making healthier choices.
It’s not just about taste and healthiness
We found that, although such decisions were determined in part by taste preferences and health considerations, they were heavily influenced by a host of other factors, many of which are outside the person’s control. These included other household members’ food preferences, family activities, workplace and time constraints, convenience and price.
Healthy eating means consuming a balanced diet rich in nutrients, including a variety of fruits, vegetables, whole grains, lean proteins and healthy fats, while limiting processed foods, added sugars and excessive salt. Healthy eating also includes how we eat and how we think about food and eating, such as having a positive relationship with food.
One 35- to 45-year-old woman, for example, said that time constraints and family preferences made it difficult to prepare healthier food:
I love the chance when I can actually get a recipe and get all of the ingredients and make it properly, but that doesn’t happen very often. It’s usually what’s there and what’s quick. And what everyone will eat.
One of the 35- to 50-year-old men also noted the extent to which family activities and children’s food preferences dictated meal choices:
Well, we have our set days where, like Wednesday nights, we have to have mackie cheese and nuggets, because that’s what the boys want after their swimming lesson.
Research shows that children are often more receptive to new foods than their parents think. However, introducing new dishes takes additional time and planning.

An 18- to 24-year-old woman discussed the role of time constraints, her partner’s activities, and price in influencing what and when she eats:
My partner plays pool on a Monday and Wednesday night, so we always have tea a lot earlier then and cook the simple things that don’t take as long, so he can have dinner before he goes rather than buying pub meals which cost more money.
Despite popular perceptions, healthy diets are not more expensive than unhealthy diets. A study comparing current (unhealthy) diets with what the Australian Dietary Guidelines recommend people should eat found that the healthy diet was 12–15% cheaper than unhealthy diets for a family of two adults and two children.
However, learning and planning to prepare new types of meals takes effort and time .
Simply educating people about what they should eat won’t necessarily result in healthier eating. People want to eat healthier, or at least know they should eat healthier, but other things get in the way .
A key to improving people’s eating behaviours is to make it easy to eat more healthily.
Policy changes to make healthy eating easier could include subsidising healthier foods such as fresh produce, providing incentives for retailers to offer healthy options, and ensuring access to nutritious meals in schools and workplaces.
So how can you make healthier food choices easier?
Here are five tips for making healthy choices easier in your household:
If certain days of the week are particularly busy, with little time to prepare fresh food, plan to cook in bulk on days when you have more time. Store the extra food in the fridge or freezer for quick preparation.
If you’re often pressed for time during the day and just grab whatever food is handy, have healthy snacks readily available and accessible. This could mean a fruit bowl in the middle of the kitchen counter, or wholegrain crackers and unsalted nuts within easy reach.
Discuss food preferences with your family and come up with some healthy meals everyone likes. For younger children, try serving only a small amount of the new food, and serve new foods alongside foods they already like eating and are familiar with.
If you rely a lot on take-away meals or meal delivery services, try making a list ahead of time of restaurants and meals you like that are also healthier. You might consider choosing lean meat, chicken, or fish that has been grilled, baked or poached (rather than fried), and looking for meals with plenty of vegetables or salad.
Remember, fruit and vegetables taste better and are often cheaper when they are in season. Frozen or canned vegetables are a healthy and quick alternative .
Read more: Cost of living: if you can't afford as much fresh produce, are canned veggies or frozen fruit just as good?
- Consumer health

Management Information Systems & Analytics – Limited Term Contract

Publications Manager

Audience Insight Officer

Academic Programs Officer, Scheduling

Director, Student Administration
- Type 2 Diabetes
- Heart Disease
- Digestive Health
- Multiple Sclerosis
- Diet & Nutrition
- Supplements
- Health Insurance
- Public Health
- Patient Rights
- Caregivers & Loved Ones
- End of Life Concerns
- Health News
- Thyroid Test Analyzer
- Doctor Discussion Guides
- Hemoglobin A1c Test Analyzer
- Lipid Test Analyzer
- Complete Blood Count (CBC) Analyzer
- What to Buy
- Editorial Process
- Meet Our Medical Expert Board
14 Benefits of Strength Training, Backed by Science
What is strength training.
- Tips to Get Started
Strength training is one of the best types of exercise for improving your overall health. In addition to building strength, it can help improve flexibility, boost metabolism , and improve the health of your organs. Strength training can also help decrease your risk of falls or injury, boost your mood, and improve your overall quality of life.
This article discusses strength training, including types of exercises, equipment, health benefits, and how to get started.
Eleganza / Getty Images
14 Benefits of Strength Training
There are many benefits of strength training. In addition to getting stronger, you can lose fat, gain muscle mass, boost your mood, and more.
1. Helps You Become Stronger
The most apparent benefit of strength training is stronger muscles. When you first start this type of training, you may notice that your strength improves quickly.
However, even though you are lifting more weight, your muscles are not getting bigger in this phase. Instead, your nervous system becomes more efficient at communicating with your muscles to recruit more muscle fibers during specific movements.
2. Promotes Greater Mobility and Flexibility
Strength training can help improve mobility and flexibility , particularly if you perform functional movements. Strength training exercises, such as squats and overhead presses, translate to daily tasks, such as squatting down to pick up an object from the floor or reaching overhead to place an item on a high shelf.
3. Burns Calories Efficiently
Strength training burns calories while you're exercising, but your body continues to burn extra calories while you're recovering. This physiological process is called postexercise oxygen consumption (EPOC).
4. Decreases Abdominal Fat
Strength training helps burn fat in the abdomen and throughout the body. Abdominal fat is a sign that fat is accumulating around your internal organs. This type of fat—visceral fat—increases your risk for serious health conditions such as heart disease, type 2 diabetes, and certain cancers.
5. Helps You Appear Leaner
Strength training can help you appear leaner by increasing your muscle mass and speeding up your metabolism, helping you burn more fat at rest. However, your diet also plays a significant role in your appearance. To build muscle mass, you must eat more calories than you burn—focused on foods high in protein and carbs.
Other factors, such as age, sex, and genetics, also affect your muscle mass.
Building muscle mass is a slow process. With consistent training and a strict diet, you can expect to gain approximately 0.5–2 pounds of muscle per month.
6. Decreases Risk of Falls
Muscle weakness can lead to balance issues, which increases your risk of falls—especially as you get older. Regularly performing strength training exercises can help reduce this risk.
7. Lowers Risk of Injury
Research has shown that athletes who perform strength exercises as a regular part of their training routine have a lower risk of injury.
8. Creates Stronger Bones
Strength training causes bones to generate more growth cells, making them stronger. This process is called osteogenesis and is specific to the body part exercised; for example, squats increase the strength of bones in the legs.
9. Improves Heart Health
Strength training can improve your heart function. It can also reduce several risk factors for heart disease, such as:
- High cholesterol
- Hyperglycemia (high blood sugar)
- Hypertension (high blood pressure)
- Having obesity
10. Improves Brain Health
Researchers have observed improved brain function immediately after a strength training workout and after regularly performing a strength training program for many weeks. This benefit applies across a lifespan, from youth to later adulthood.
Strength training can improve the brain's executive functions, such as attention span, memory, and problem-solving.
11. Helps Balance Blood Sugar Levels
Strength training helps the body maintain healthy blood sugar levels and increases insulin sensitivity. Insulin is the hormone that helps the body convert glucose (sugar) into energy. Chronically high blood sugar levels can lead to type 2 diabetes , which can lead to permanent nerve damage and other health complications.
12. Boosts Your Mood
Strength training can boost your mood. During high-effort exercises, the brain releases "feel good" chemicals called endorphins. Researchers have found that strength training can decrease depressive symptoms in people who have been diagnosed with anxiety or depression.
13. Boosts Self-Esteem
Researchers have shown that strength training can positively affect self-esteem and body image. One study of the impact of resistance training on self-esteem among youth found positive associations between resistance training and overall self-worth, physical self-worth, and perceived physical strength. However, the study authors call for more rigorous research before drawing any definitive conclusions.
14. Promotes a Better Quality of Life
Strength training has been shown to improve overall quality of life, though its impact varies across populations and among those with certain health conditions. One systematic review found that resistance training contributes to improved mental health and pain reduction, improving quality of life.
Many types of training fall under the umbrella of strength training. Examples include:
- Muscular hypertrophy : Training to build muscle mass
- Muscular endurance : Training to exercise your muscles for longer periods
- Circuit training : Performing a variety of exercises in a specific pattern (called a circuit) typically to target muscles throughout the body in a single workout
- Maximum muscular strength : Training to increase the maximum amount of weight you can lift for one repetition of a specific exercise
- Explosive power : Training to produce a large amount of muscle force quickly
- Agile strength : Training your muscles in an environment in which you have to start and stop quickly and perform movements in multiple directions
- Speed strength : Training your muscles to perform movements at a faster pace
People use various types of equipment for strength training:
- Free weights
- Body weight (using the weight of your body as resistance, for example, while doing push-ups)
- Body-weight suspension systems
- Cable machines
- Kettlebells
- Resistance bands
Tips to Get Started With a Strength Training Routine
When starting a strength training routine, it's important to do it correctly to reduce injury risk.
Start With the Basics
Start simple with strength training exercises. Pick a few exercises to begin with, and take some time to get into a routine before adding more. Explore online videos to help you get started at home.
Choose an Appropriate Load and Volume
When beginning a new strength training routine, use light weights, such as small dumbbells. Or, try bodyweight resistance exercises that don't require equipment, such as sit-ups, push-ups, squats, and lunges.
Avoid Overdoing It
When you start strength training, do less than you think you can. You might feel fine during your workout, but that doesn't mean you won't be sore. Muscle soreness can develop 12 to 72 hours after you've exercised—a concept called delayed onset muscle soreness (DOMS).
How Often Should You Strength Train?
The Centers for Disease Control and Prevention (CDC) recommends that adults perform strength training exercises twice weekly. However, you may benefit from strength training more frequently, especially if you exercise different muscle groups on different days. Make sure to have at least one day of rest between workouts for the same body parts.
Is Strength Training Safe for Everyone?
As with any new exercise program, you should check with a healthcare provider before you start strength training—especially if you have any injuries or medical conditions.
For example, strength training could cause serious injury for someone diagnosed with osteoporosis —a condition that causes weakening of the bones.
If you have an injury or medical condition, a healthcare provider might recommend that you begin strength training under the supervision of a physical therapist who can determine which exercises are safe for you.
If you are healthy but want more direction with your strength training, consider working with a certified personal trainer .
Strength training offers many benefits, both for the body and the mind. In addition to stronger muscles, it strengthens your bones and heart, helps balance blood sugar levels, and decreases your risk of falls or injuries. It can also boost mood and improve overall quality of life. Check with a healthcare provider before starting a new exercise routine to ensure strength training is safe for you.
American Council on Exercise. How muscle grows .
American Council on Exercise. 7 things to know about excess post-exercise oxygen consumption (EPOC) .
Harvard Health Publishing. Abdominal fat and what to do about it .
Hopewell S, Adedire O, Copsey BJ, Boniface GJ, Sherrington C, Clemson L, Close JC, Lamb SE. Multifactorial and multiple component interventions for preventing falls in older people living in the community . Cochrane Database Syst Rev. 2018 Jul 23;7(7):CD012221. doi: 10.1002/14651858.CD012221.pub2
Stephenson SD, Kocan JW, Vinod AV, Kluczynski MA, Bisson LJ. A comprehensive summary of systematic reviews on sports injury prevention strategies . Orthop J Sports Med . 2021 Oct 28;9(10):23259671211035776. doi: 10.1177/23259671211035776
Benedetti MG, Furlini G, Zati A, Letizia Mauro G. The effectiveness of physical exercise on bone density in osteoporotic patients . Biomed Res Int . 2018;2018:4840531. doi:10.1155/2018/4840531
Jafarikhah R, Damirchi A, Rahmani Nia F, Razavi-Toosi SMT, Shafaghi A, Asadian M. Effect of functional resistance training on the structure and function of the heart and liver in patients with non-alcoholic fatty liver . Sci Rep . 2023;13(1):15475. doi:10.1038/s41598-023-42687-w
Herold F, Törpel A, Schega L, Müller NG. Functional and/or structural brain changes in response to resistance exercises and resistance training lead to cognitive improvements - a systematic review . Eur Rev Aging Phys Act . 2019;16:10. doi:10.1186/s11556-019-0217-2
American Diabetes Association. Anaerobic exercise and diabetes .
Mahindru A, Patil P, Agrawal V. Role of physical activity on mental health and well-being: a review . Cureus . 2023;15(1):e33475. doi:10.7759/cureus.33475
Gordon BR, McDowell CP, Hallgren M, Meyer JD, Lyons M, Herring MP. Association of efficacy of resistance exercise training with depressive symptoms: meta-analysis and meta-regression analysis of randomized clinical trials . JAMA Psychiatry . 2018 Jun 1;75(6):566-576. doi: 10.1001/jamapsychiatry.2018.0572
Collins H, Booth JN, Duncan A, Fawkner S, Niven A. The effect of resistance training interventions on 'the self' in youth: a systematic review and meta-analysis . Sports Med Open . 2019;5(1):29. doi:10.1186/s40798-019-0205-0.
Marquez DX, Aguiñaga S, Vásquez PM, et al. A systematic review of physical activity and quality of life and well-being . Transl Behav Med . 2020;10(5):1098-1109. doi:10.1093/tbm/ibz198
Hart PD, Buck DJ. The effect of resistance training on health-related quality of life in older adults: systematic review and meta-analysis . Health Promot Perspect . 2019;9(1):1-12. doi:10.15171/hpp.2019.01.
The National Strength and Conditioning Association. Basics of strength and conditioning manual .
American Council on Exercise. 7 different types of strength and their benefits .
Kaiser Permanente. Simple ways to get started with strength training .
American College of Sports Medicine. Delayed onset muscle soreness (DOMS) .
Centers for Disease Control and Prevention. Physical activity for adults: an overview .
National Institutes of Health. Osteoporosis .
By Aubrey Bailey, PT, DPT, CHT Dr, Bailey is a Virginia-based physical therapist and professor of anatomy and physiology with over a decade of experience.
Healthy Food Essay for Students and Children
500+ words essay on healthy food.
Healthy food refers to food that contains the right amount of nutrients to keep our body fit. We need healthy food to keep ourselves fit.
Furthermore, healthy food is also very delicious as opposed to popular thinking. Nowadays, kids need to eat healthy food more than ever. We must encourage good eating habits so that our future generations will be healthy and fit.
Most importantly, the harmful effects of junk food and the positive impact of healthy food must be stressed upon. People should teach kids from an early age about the same.

Benefits of Healthy Food
Healthy food does not have merely one but numerous benefits. It helps us in various spheres of life. Healthy food does not only impact our physical health but mental health too.
When we intake healthy fruits and vegetables that are full of nutrients, we reduce the chances of diseases. For instance, green vegetables help us to maintain strength and vigor. In addition, certain healthy food items keep away long-term illnesses like diabetes and blood pressure.
Similarly, obesity is the biggest problems our country is facing now. People are falling prey to obesity faster than expected. However, this can still be controlled. Obese people usually indulge in a lot of junk food. The junk food contains sugar, salt fats and more which contribute to obesity. Healthy food can help you get rid of all this as it does not contain harmful things.
In addition, healthy food also helps you save money. It is much cheaper in comparison to junk food. Plus all that goes into the preparation of healthy food is also of low cost. Thus, you will be saving a great amount when you only consume healthy food.
Get the huge list of more than 500 Essay Topics and Ideas
Junk food vs Healthy Food
If we look at the scenario today, we see how the fast-food market is increasing at a rapid rate. With the onset of food delivery apps and more, people now like having junk food more. In addition, junk food is also tastier and easier to prepare.
However, just to satisfy our taste buds we are risking our health. You may feel more satisfied after having junk food but that is just the feeling of fullness and nothing else. Consumption of junk food leads to poor concentration. Moreover, you may also get digestive problems as junk food does not have fiber which helps indigestion.
Similarly, irregularity of blood sugar levels happens because of junk food. It is so because it contains fewer carbohydrates and protein . Also, junk food increases levels of cholesterol and triglyceride.
On the other hand, healthy food contains a plethora of nutrients. It not only keeps your body healthy but also your mind and soul. It increases our brain’s functionality. Plus, it enhances our immunity system . Intake of whole foods with minimum or no processing is the finest for one’s health.
In short, we must recognize that though junk food may seem more tempting and appealing, it comes with a great cost. A cost which is very hard to pay. Therefore, we all must have healthy foods and strive for a longer and healthier life.
FAQs on Healthy Food
Q.1 How does healthy food benefit us?
A.1 Healthy Benefit has a lot of benefits. It keeps us healthy and fit. Moreover, it keeps away diseases like diabetes, blood pressure, cholesterol and many more. Healthy food also helps in fighting obesity and heart diseases.
Q.2 Why is junk food harmful?
A.2 Junk food is very harmful to our bodies. It contains high amounts of sugar, salt, fats, oils and more which makes us unhealthy. It also causes a lot of problems like obesity and high blood pressure. Therefore, we must not have junk food more and encourage healthy eating habits.
Customize your course in 30 seconds
Which class are you in.

- Travelling Essay
- Picnic Essay
- Our Country Essay
- My Parents Essay
- Essay on Favourite Personality
- Essay on Memorable Day of My Life
- Essay on Knowledge is Power
- Essay on Gurpurab
- Essay on My Favourite Season
- Essay on Types of Sports
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Download the App


Student Health and Wellbeing
The importance of exercise
Recently, I went to watch a few of my friends complete the 10K Barossa Marathon that they had been practising and preparing for over the past few months. Watching them cross the finish line was incredibly satisfying and inspiring.
As a child, I always despised running. I blamed my lack of speed and endurance on my non-existent calves and iron deficiency. After high school, with no one forcing me to run, I simply stopped. Every gym session was purely weight training with no cardio whatsoever. I declined every invitation to go on a run by simply saying, “I’m not built for it.”
Several months ago, a few of my friends decided they were entering their "running era," whatever that meant. Every morning, they would wake up at ungodly hours to go for a run before class. By the time I was awake, they would be back home, faces red with exhaustion and completely puffed out. I remember looking at them and thinking to myself, “Why would you do that to yourself?” But despite the exhaustion and pain, they always had an accomplished grin on their faces as they discussed how much their pace had improved from the previous run.
Curiosity got the best of me, and I started to wonder if there was more to this running thing than I had thought. Studies have shown that people who regularly exercise have better mental health and emotional wellbeing. Exercise not only boosts our mood, concentration, and alertness but also improves our cardiovascular and overall physical health.
Inspired by my friends, I decided to give running a try. I started slow, with short distances and a comfortable pace. At first, it was tough. My legs ached, my lungs burned, and I felt like giving up. But I kept at it, motivated by the visible improvements my friends had achieved and their constant encouragement.
As the weeks went by, something amazing happened. I started to notice changes—not just in my physical health, but in my mental wellbeing as well. The more I ran, the better I felt. My stress levels dropped, my mood lifted, and I found myself more focused and alert during classes. I even started to sleep better, waking up feeling more refreshed and ready to tackle the day.
Running also became a social activity. Joining my friends on their morning runs created a sense of camaraderie and support. We celebrated each other's progress, shared tips, and motivated one another to keep going. It turned what once felt like a solitary, gruelling activity into a fun and rewarding experience.
So, if you’re feeling overwhelmed, stressed, or just looking for a way to improve your mental and physical health, I encourage you to give exercise a try. You don't have to start with a marathon—just find an activity you enjoy and stick with it. Your mind and body will thank you.
- Previous page
Home — Essay Samples — Nursing & Health — Eating Habits — Nutrition and Diet: Importance of Healthy Eating Habits
Nutrition and Diet: Importance of Healthy Eating Habits
- Categories: Eating Habits Healthy Food
About this sample

Words: 992 |
Published: Feb 12, 2019
Words: 992 | Pages: 2 | 5 min read

Cite this Essay
Let us write you an essay from scratch
- 450+ experts on 30 subjects ready to help
- Custom essay delivered in as few as 3 hours
Get high-quality help

Prof. Kifaru
Verified writer
- Expert in: Nursing & Health

+ 120 experts online
By clicking “Check Writers’ Offers”, you agree to our terms of service and privacy policy . We’ll occasionally send you promo and account related email
No need to pay just yet!
Related Essays
2 pages / 989 words
2 pages / 1019 words
2 pages / 1017 words
1 pages / 2391 words
Remember! This is just a sample.
You can get your custom paper by one of our expert writers.
121 writers online

Still can’t find what you need?
Browse our vast selection of original essay samples, each expertly formatted and styled
Related Essays on Eating Habits
Campbell, B., Kreider, R. B., Ziegenfuss, T., La Bounty, P., Roberts, M., Burke, D., ... & Antonio, J. (2007). International Society of Sports Nutrition position stand: protein and exercise. Journal of the International Society [...]
Fung, Jason, and Jimmy Moore. 'The Complete Guide to Fasting.' Victory Belt Publishing, 2016.Fung, Jason. 'The Obesity Code: Unlocking the Secrets of Weight Loss.' Greystone Books, 2016.Mattson, Mark P., Rafael de Cabo, and [...]
Healthy carob bars have gained attention as a potential substitute for traditional chocolate products. As a college student studying marketing, it is important to recognize the potential of healthy carob bars and develop a [...]
Eating habits are an integral part of human life, as they directly impact our physical health, emotional well-being, and overall quality of life. As an individual, my eating habits have evolved over the years due to various [...]
In Radley Balko’s essay “What You Eat Is Your Business,” he argues that what we put into our bodies is our business, and it is our responsibility to make healthy choices. The widespread epidemic of obesity can only be solved if [...]
Food insecurity is a complex and multifaceted issue that requires urgent attention and action. By understanding the causes and consequences of food insecurity, we can develop effective strategies and solutions to address this [...]
Related Topics
By clicking “Send”, you agree to our Terms of service and Privacy statement . We will occasionally send you account related emails.
Where do you want us to send this sample?
By clicking “Continue”, you agree to our terms of service and privacy policy.
Be careful. This essay is not unique
This essay was donated by a student and is likely to have been used and submitted before
Download this Sample
Free samples may contain mistakes and not unique parts
Sorry, we could not paraphrase this essay. Our professional writers can rewrite it and get you a unique paper.
Please check your inbox.
We can write you a custom essay that will follow your exact instructions and meet the deadlines. Let's fix your grades together!
Get Your Personalized Essay in 3 Hours or Less!
We use cookies to personalyze your web-site experience. By continuing we’ll assume you board with our cookie policy .
- Instructions Followed To The Letter
- Deadlines Met At Every Stage
- Unique And Plagiarism Free

IMAGES
VIDEO
COMMENTS
4 Pages. Open Document. Exercise and eating healthy are two of the most important things you need to do to take care of your body properly. Both exercise, and eating healthy, have many advantages and benefits. They help with multiple things needed throughout your life. These things include growing physically, mentally, and if you are religious ...
Answer 1: Exercise helps people lose weight and lower the risk of some diseases. When you exercise daily, you lower the risk of developing some diseases like obesity, type 2 diabetes, high blood pressure and more. It also helps to keep your body at a healthy weight.
See here the importance of a healthy diet during times of Covid-19. Eating a healthy balanced diet accompanied by regular exercise is essential in maintaining physical and mental health and well-being. Not only are these effective in preventing excess weight gain or in maintaining weight loss, but healthier lifestyles are also associated with improved sleep and mood.
Healthy Eating and Cognitive Function. Healthy eating habits are also crucial for cognitive function. Nutrients like Omega-3 fatty acids, antioxidants, and B vitamins, which are found in foods like fish, nuts, fruits, and vegetables, are essential for brain health. They enhance memory, improve mood, and protect against cognitive decline.
The benefits of exercise are vast and well-documented. Regular physical activity has been shown to improve physical health, reduce the risk of chronic diseases, and enhance mental well-being. While barriers to exercise such as lack of time and motivation exist, it is important to recognize that even small amounts of physical activity can have ...
Overwhelming evidence exists that lifelong exercise is associated with a longer health span, delaying the onset of 40 chronic conditions/diseases. What is beginning to be learned is the molecular mechanisms by which exercise sustains and improves quality of life. The current review begins with two short considerations.
Here are some other benefits you may get with regular physical activity: Helps you quit smoking and stay tobacco-free. Boosts your energy level so you can get more done. Helps you manage stress and tension. Promotes a positive attitude and outlook. Helps you fall asleep faster and sleep more soundly.
Healthy Lifestyle and Eating Essay. Healthy eating is the process of keeping the body clean, strong, and healthy at all times (Allen, 1926). Healthy living, on the other hand, means that one should be able to eat the right food, get enough exercise, and maintain cleanliness (James, 1907). Unfortunately, many people do not keep track of these ...
essay based on the theme of "living well." Coming from a hard childhood, I have always turned to exercise to release any negativity I felt, which is what inspired me to write about this topic. ... "The Importance of Healthy Eating and Exercise" 3 John Kearney, Michael Gibney, and J. Alfredo Martinez, unveils that 73.6% of the tested
Potassium helps your body release sodium and can help ease the tension in your blood vessels, according to the AHA. This naturally helps lower your blood pressure. Exercise also helps to take that blood pressure down by naturally releasing nitric oxide. Nitric oxide is known as a vasodilator, which means it opens up your blood vessels, helping ...
Healthy food habit prevents various diseases. Reducing the amount of fat in the diet prevents cholesterol and heart diseases. Get the huge list of more than 500 Essay Topics and Ideas. Impact of Exercise on our Health. Routine exercise helps improve our muscle power. Exercise helps in good oxygen supply and blood flow throughout the body.
In conclusion, eating a balanced diet and exercising regularly are both super important for keeping your body healthy and happy. Just like a superhero needs the right gadgets, your body needs the right foods and exercise to be at its best. Remember to eat a variety of foods and to play and move around every day.
This essay has explored the various ways in which individuals can be persuaded to eat healthy, as well as the potential consequences of neglecting this crucial aspect of our lives. By taking proactive steps to improve our diet, we can lead healthier and happier lives. In today's fast-paced world, the importance of eating healthy has never been ...
Proper nutrition and physical activity are crucial for maintaining a healthy lifestyle and reducing the risk of chronic diseases. Unhealthy eating habits and a lack of exercise can lead to serious health conditions such as diabetes, obesity, stroke, heart disease, and osteoporosis.A study conducted in 1990 found that 14% of all deaths in the U.S. were attributed to poor eating habits and ...
Healthy Eating & Physical Activity for Life. Consuming healthy foods and beverages, along with getting regular physical exercise, may help you reach and maintain a weight that suits you. Maintaining that weight, getting adequate sleep, and managing stress may also help prevent some health problems. This series offers tips for developing and ...
100 Words Essay on Nutrition And Exercise Importance of Nutrition. Eating healthy foods gives your body the energy it needs to work well. Imagine your body like a car. Without the right fuel, a car won't run smoothly. For us, good food is our fuel. Fruits, vegetables, grains, protein, and dairy give us vitamins and energy.
Physical inactivity is a modifiable risk factor (similar to dyslipidemia and hypertension) for a variety of chronic diseases, including cancer and cardiovascular disease. Exercise provides a clear health benefit, which serves in the primary and secondary prevention of these disease processes (the most important being a reduction in cardiovascular disease and premature death). The physiologic ...
Healthy eating also includes how we eat and how we think about food and eating, such as having a positive relationship with food. One 35- to 45-year-old woman, for example, said that time ...
The Role of Fruits, Vegetables, and Proteins. A healthy diet should also include an adequate intake of fruits and vegetables. These foods provide essential micronutrients, such as vitamins, that are necessary for optimal health. Fruits and vegetables are particularly important in preventing ischaemic heart disease, gastrointestinal cancer ...
In Conclusion, Eating healthy and exercise is important when having a healthy lifestyle. Exercise can also help with many other things such as helping with relaxation, sleep quality and it increases your energy level. As a result, exercise and eating healthy is a way to reduce the risk of disease, create a healthy lifestyle, and avoid obesity.
Not only nutrition is important for physical well being it is important to work out and exercise. A healthy diet is a balanced diet which includes food from all the major food groups in the right proportions, and in quantities which maintain healthy body weight. ... Autoethnography of Eating Habits Essay. Eating habits are an integral part of ...
13. Boosts Self-Esteem . Researchers have shown that strength training can positively affect self-esteem and body image. One study of the impact of resistance training on self-esteem among youth found positive associations between resistance training and overall self-worth, physical self-worth, and perceived physical strength.
500+ Words Essay on Healthy Food. Healthy food refers to food that contains the right amount of nutrients to keep our body fit. We need healthy food to keep ourselves fit. Furthermore, healthy food is also very delicious as opposed to popular thinking. Nowadays, kids need to eat healthy food more than ever. We must encourage good eating habits ...
Curiosity got the best of me, and I started to wonder if there was more to this running thing than I had thought. Studies have shown that people who regularly exercise have better mental health and emotional wellbeing. Exercise not only boosts our mood, concentration, and alertness but also improves our cardiovascular and overall physical health.
It also nourishes and nourishes the skin. So always be careful when using oil. The last healthy eating habit is to prepare food for a nutrition list. It is better to eat a homemade meal whenever conceivable and avoid snacks. Thus, every meal of the day can be adjusted based on nutrition.