sample application letter for provident loan

WTO / Applications / 20 Best Loan Application Letter Samples (Guide and Format)

20 Best Loan Application Letter Samples (Guide and Format)

An application letter for a loan is a formal letter written to a financial institution by a borrower requesting a loan, payable in a specified amount of time.

The letter helps lenders get acquainted with the borrowers better to determine if they qualify for the loan based on the information provided or not. Writing it is important because it helps convince lending institutions to lend you a specific amount of money. It is their first impression of you, which is why it should be written with great care. In this article, we will guide you on how to write it, the type of information you should provide, and some pointers that will help you highlight your strengths in the letter.

Brief Overview- What to Include

There are no strict rules for writing an application for a loan. It depends on the borrower to decide what information to include, but the following items are typically included in it:

• Contact information
• Explanation of why money is needed
•  Amount of money being requested
• Purpose of the money
• Details about employment history
• Personal references
• Company information
•  A list of supporting documents

When to Write?

Two main situations warrant this letter. The first instance is when you are seeking a loan from a conventional bank lender. Conventional bank lenders are financial institutions that do not offer loans but make them available to the general public. Conventional banks usually require applicants to submit this application to prove their creditworthiness.

The second situation that warrants its use is when applying for an SBA-guaranteed loan. An SBA-guaranteed loan involves the federal government; applicants must undergo additional screening before they are approved for funding. Applicants can improve their chances of getting an SBA guarantee by submitting a personalized, formal loan application with supporting documentation.

There are situations when you do not necessarily need to write this letter, such as when you are borrowing from friends and family, from an alternative lender who may only require your bank statements or pay slips, when seeking equipment financing, and lastly when you are requesting a business line of credit.

Free Templates

Pre-writing Considerations

Applying for a loan involves being prepared for anything, so it is important to have the things you need before writing. Do some research on your lender, and write down notes about why they are suitable for you and what you would like them to know about your project. Write those questions that may arise during the process of applying for your loan. Check your credit score and know your rights as a borrower when you apply for a loan.

After you have done all of the above, review everything and ensure that what you’ve written is easy to understand by someone who has not read your notes or audited your finances. When applying for a loan in a major financial institution or applying for an SBA loan, you will almost always be required to write an application letter for a loan. It is important to note that unless it is supported by a sound credit situation or proper financial planning, it may not be enough to help you secure the loan. 

Fortunately, there are two things that you can do to increase your loan limit and increase your chances of getting a loan. You can first check your business and personal credit scores from accredited credit reporting bureaus such as TransUnion, Equifax, and Experian and take the necessary steps to improve them.

The second thing that you can do is to prepare your business financial statements, i.e., your profit and loss statement, cash-flow statement, balance statement, etc., for the past six months and attach them to your letter. These documents are essential when applying for a loan as they help the financial institution assess your creditworthiness and increase your chances of securing a loan.

How to Write a Loan Application?

Writing it can seem daunting, but it can be a simple process if you follow the proper format and include all the required information.

The following is a summary of the information you must provide in your letter:

The header is an integral part of the standard business letter format. It should include:

• Your name and contact information : Make sure to include your full name, address, and contact information. This should include a mailing address with a zip code, a business email address, and your cell phone number where you can be reached.
• The date : Include the month, day, and year of the letter. You must ensure that you write the date on which the letter was created.
• The name of the recipient : This will be a bank representative in many cases, but it can also be an SBA representative or another financial institution to whom the borrower is addressing the letter.

Subject line

When writing it, make sure to include a clear subject line that will help the recipient understand the purpose of the letter. Make sure to include whether the loan is for personal or professional use in the subject line.

“Loan Request Application Letter.”

Address your letter correctly. If you do not know who will be reading it, write “ To Whom It May Concern .” If you are trying to get a business loan, address it to the company’s representative issuing the loan. If you are applying for a personal loan, address it to the bank or whoever provides it.

Introduction

It should begin with a brief statement of the goal and amount you are requesting. It should also state your qualifications for the loan and any other pertinent information that can be used for your evaluation as a borrower such as your financial status, your work history, the length of time you have been in business, etc.

The body is the main part of the letter, and it should contain all the information the recipient will need to decide whether to grant the loan or deny the request.

Some of the information that must be covered in the body includes:

• Basic business information : If you are writing it, the first item to include in the body of the letter is details about your business. This information will help the lender understand who you are and will serve as the foundation for your loan application. Some of the information that you should cover in this section includes your business’s registered name, business type (i.e., partnership , sole proprietorship, LLC , etc.), nature of your business (i.e., what you do), main services and products, your business model, the number of employees that you have, and your annual generated revenue.
• The purpose of the loan : You must explain why you need the loan and the purpose for which it is being requested. This can be to purchase or expand a business, for a personal reason, or to pay some debt.
• Present yourself as being trustworthy : To get a loan, you need to establish trust with the lender. This can be achieved by explaining what you do for a living, providing some identity documents, and demonstrating why you deserve to be trusted.
• Explain how you intend to pay back : Explain briefly how you plan on repaying the loan. This should include a timeline for repayment and be supported by evidence such as a business plan, personal financial statement, or credit report .
• Proof of financial solvency : In some cases, you will be asked to provide evidence that the funds requested are not your only source of income. Documents like bank statements or tax returns can help you prove that you have other sources of funding, which will increase the likelihood that your request will be granted.

In the conclusion, you must thank the lender for considering your request. Briefly mention all the attached financial documents. Remember that each lender has their own set of loan application requirements and may request different information or documentation from borrowers, so make sure to double-check the specific instructions provided by the lender.

Once you have finished writing the letter, be sure to sign it at the bottom. You may include phrases such as:

“Respectfully yours” or “Sincerely yours”.

Place your name and contact information directly above the signature line.

SBA Loan Application Letter Template

[Your Name]

[Your Address]

[City, State ZIP Code]

[Your Phone Number]

[Your Email Address]

[Loan Officer’s Name]

[Bank Name]

[Bank Address]

Dear [Loan Officer’s Name],

I am writing to apply for a Small Business Administration (SBA) loan to help fund my [business name]. I am excited to have the opportunity to present my business plan to you and explain why I believe my business is a great candidate for an SBA loan.

[Provide an introduction to your business, including its history, products or services offered, and unique selling proposition. Explain why you started the business and what sets it apart from competitors. This should be no more than two paragraphs.]

I am seeking an SBA loan in the amount of [$ amount], which will be used to [briefly explain how the funds will be used]. My business has experienced steady growth in recent years, but we need additional capital to take advantage of new opportunities and expand our reach.

[Provide a detailed explanation of how you plan to use the funds, including any expected return on investment. Be specific about the amount of money you need, how long you will need it for, and how it will be used.]

As part of my loan application, I have included the following documents for your review:

• Business plan
• Financial statements for the past three years
• Tax returns for the past three years
• Cash flow projections
• Articles of incorporation
• Personal financial statements for all owners

A list of collateral that will be used to secure the loan, if applicable

[Provide a comprehensive list of all the documents you have included with your application. Make sure you have included everything the bank has asked for, and any additional documents that may be relevant.]

I am confident in the future success of my business and believe that an SBA loan is the right choice for us. I understand that the loan application process can be lengthy, and I am committed to providing any additional information or documentation that may be required to support my application.

Thank you for considering my loan application. I look forward to hearing from you soon.

Loan Application Letter Sample

Make your small business loan application more polished with our simple sample letters. They’re crafted to help you convey your needs professionally and improve the impact of your request. 

Sample letter 1

Dear Sir/Madam,

I am writing to apply for a Small Business Administration loan to support my growing business, GreenTech Innovations. Established in 2018, we specialize in eco-friendly technology solutions. Our recent market analysis indicates significant growth potential in sustainable energy products.

To capitalize on this opportunity, we require additional funding for research and development, marketing, and expanding our team. An SBA loan would enable us to invest in these critical areas, fostering innovation and job creation. Our business plan, attached to this application, outlines our strategy for a sustainable and profitable future.

GreenTech Innovations has a strong financial track record, with consistent revenue growth over the past three years. We have maintained a healthy cash flow and have a solid plan for loan repayment, as detailed in our financial projections. Our commitment to financial responsibility and strategic growth makes us an ideal candidate for an SBA loan.

Thank you for considering our application. We are committed to contributing positively to the economy and the environment. Your support would be instrumental in helping us achieve our goals.

Jordan Smith

Owner, GreenTech Innovations

Sample letter 2

Dear Business Loan Officer,

I am reaching out to request a business loan for my company, Bella’s Boutique, a unique clothing and accessories store located in downtown Springfield. Since our opening in 2019, we have become a beloved part of the local community, known for our exclusive designs and personalized customer service.

This loan is sought to enhance our inventory, upgrade our in-store technology, and expand our online presence. These improvements are essential for keeping pace with the evolving retail landscape and meeting the growing demands of our customers. Our detailed business plan is attached for your review.

Financially, Bella’s Boutique has demonstrated resilience and growth, even amid challenging economic times. Our sales figures have shown a steady increase, and we have a clear plan for managing the loan and ensuring its repayment. We believe these factors make us a strong candidate for a loan.

Your consideration of our loan application is greatly appreciated. This funding will not only help Bella’s Boutique thrive but will also support the local economy by providing more employment opportunities and enhanced retail experiences.

Thank you for your time and consideration.

Warm regards,

Isabella Martinez

Founder, Bella’s Boutique

The effectiveness of these sample letters as a guide for someone seeking to write a loan application lies in several key aspects. Firstly, they demonstrate the importance of a clear and concise introduction, where the purpose of the letter is immediately stated, ensuring the reader understands the intent from the outset. This is crucial in any formal business communication. Both samples skillfully describe the nature and background of the respective businesses, providing just enough detail to give the reader a sense of the company’s identity and market position without overwhelming them with unnecessary information. This balance is vital in maintaining the reader’s interest and establishing the context of the request.

Moreover, the letters excel in explicitly stating the purpose of the loan, which is a critical component of any loan application. They outline how the funds will be utilized to grow and improve the business, demonstrating not only a clear vision but also a strategic approach to business development. This helps in building a sense of trust and reliability with the lender. Furthermore, the inclusion of financial health indicators, such as past revenue growth, cash flow management, and a repayment plan, adds to this trust by showing financial responsibility and foresight.

The writers also incorporate attachments like business plans and financial projections, which provide additional depth and substantiation to their claims. This shows thorough preparation and professionalism, which are highly regarded in the business world. Finally, the tone of the letters is appropriately formal yet approachable, and they conclude with a note of gratitude, reflecting good business etiquette. This combination of clarity, conciseness, relevance, and professionalism makes these letters exemplary guides for anyone looking to draft an effective and persuasive business loan application.

Tips for Writing

Following are some tips for writing this letter:

Be specific

Be sure to include specific details in it to keep the reader’s attention. Ensure that you include information about the purpose of the loan, how much money you need, and the reason why you are a good candidate for a loan.

Brevity is essential when writing this letter. Stick to the essential points and avoid extraneous details. This will help to ensure that your letter is easy to read and that the reader is not distracted by irrelevant information.

Address the appropriate person

Ensure that you address your letter to the most relevant party for your particular situation.

Consider contacting the bank to find out to whom it should be addressed. This is how you can be sure that it will get to the right person.

Use a proper format and layout

As with all letters, you should use clear, concise paragraphs and avoid unnecessary jargon. Make sure to use the appropriate format for formal letter writing and use a professional, polished layout.

Include business financial statements

The financial statements for your company must be attached to your letter if you are a business owner. In this way, the reader will better understand your overall financial situation and help demonstrate that you are a good candidate for a loan.

The following are some of the purposes for which you may request a small business administration loan: to start a new business, to buy new equipment or inventory for your company, to upgrade or expand an existing business, to cover unanticipated expenditures, to pay off high-interest debt, to fund marketing campaigns, to move your office to a new location, to buy insurance for your business, to purchase stock, to buy out shareholders, and for any other lawful reason authorized by the lender.

Key Takeaways

Here are the key takeaways from this article:

• When writing an application for a loan, be sure to provide specific details about the purpose of the loan, how much money you need, and why you are a good candidate for a loan.
• Use the standard business letter format and use clear, concise paragraphs.
• Brevity is vital when writing such a document, so mention only the essential points and avoid extraneous details.
• Address your letter to the most relevant party for your situation, and be sure to include your company’s financial statements.

About This Article

Was this helpful?

Great! Tell us more about your experience

Not up to par help us fix it, keep reading.

Applications , Forms

40 free credit application forms and samples.

Free Volunteer Application Forms (Templates) – Word, PDF

Applications , Employment

20+ blank leave application forms (free templates).

55 Blank Rental Application Forms – Templates – Editable

Thank you for your feedback.

Your Voice, Our Progress. Your feedback matters a lot to us.

Applications , Request Letters

Loan Request Letter (Format & Sample Applications)

A Loan Request Letter is a letter written by a loan applicant and addressed to a lending institution, generally sent as a part of the loan application process. A loan request letter introduces you to the bank or other lending institution, clearly describes your planned use for the loan funds, and describes how you will pay back the loan. It is the part cover letter and part resume because you demonstrate the qualities that make you a good candidate for a loan by outlining your qualifications.

Anyone who applies for personal or business loan should write a loan request letter and enclose it with their loan application. This letter is often the lending institution’s first impression of you as a borrower. Therefore, it should be professional, clear, and concise, easily fitting into one page.

Important: Write using a professional format and in a professional tone. Banks and other lending organizations are concerned about your ability to repay the loan. Pointing out your financial problems works against you – instead, point out your qualifications as a borrower. Remember, this letter is your first contact with the lender and uses it to showcase your company as a reliable borrower.

What a Lender Needs to Know

In order to consider your loan request, a lender needs some information about you or your company. Although this information is included in detail in your loan application, your letter should formally introduce your request. Here is what you should include in your loan request letter:

• Your name and/or your company name, including any DBA
• Your contact information
• Your business entity structure
• Brief description of your business
• Your number of employees
• How long you have been in operation
• Annual revenue and profits if your company is profitable
• Amount of loan requested
• How the funds will be spent
• Your financial security
• A list of enclosures

The bank or lending institution is primarily concerned with how the money they are lending will be spent and repaid. Be sure to include information on these two critical points in your letter.

In addition to the loan application, you should enclose applicable financial documents, such as tax returns. Send your business plan, cash flow statement, and profit and loss (P&L) statement.

Loan Request Letter (Format)

{your name}

{your company’s name}

{your address}

{lender name}

{lender title}

{lender institution name}

{lender address}

RE: {(Small business) or (Personal)} loan request for {amount}

Dear {lender name}:

The purpose of this letter is to request a {(small business) or (personal)} loan in the amount of {amount} for the purpose of {purpose}. {Use this space to discuss your small business. Include name, business structure, and industry.}

{Business name} began operation on {date}, with {number} employees. As a {business structure type}, {business name} has consistently grown and now employs {number} individuals. {Use this space to discuss your marketing presence.}

{Use this area to briefly discuss your most recent year’s revenue and profit, if profitable. Discuss revenue and profit consistently over time when possible.}

{Use this area to describe the reason for the loan request.} {Use this area to explain that the opportunity is immediately available, but you lack sufficient immediate funds.}

Attached, please find our business plan, our annual profit and loss statement, and our most recent cash flow statement for your review. These financial documents and our strong credit score of {number} combine to make us a safe credit risk for {lending institution name}.

I would greatly appreciate the opportunity to speak with you about a {(small business) or (personal)} loan. I can be reached at {phone number} or by email at {email address}.

Thank you for your time and your consideration of my request.

{your signature}

Sample Loan Application Letter

Matthew Dobney

Entirely Electronics

3048 West First Street

Spavinah, OK 89776

EntirelyElectronics.com

June 22, 2048

Mr. James Burrows

SBA Loan Administrator

Bank of American Businesses

New York, NY 65782

RE: Small business loan request for $20,000

Dear Mr. Burrows:

The purpose of this letter is to request a small business loan in the amount of $20,000 for the purpose of enlarging our warehouse.

Entirely Electronics began operation on June 1, 2020, with two employees. As a partnership, Entirely, Electronics has consistently grown and now has 20 full-time employees. Entirely Electronics has been quite successful in obtaining a proportionate share of the online electronic retail community. Our online presence has grown from our website alone to Facebook, Instagram, and Yelp. Our marketing techniques consistently drive new customers to Entirely Electronics, and we boast a high customer retention rate.

Last year, Entirely, Electronics saw a growth of 25% in revenue over the previous year. Our profit margin remained stable at 18% throughout the year.

Our growth has created a significant shortage of available warehouse space, and market research shows we will continue to grow. As we look to the future, we understand we must create more warehouse space to continue growing. Although our revenue is consistent, we do not have the immediate large amount needed to complete the necessary expansions to our warehouse.

Attached, please find our business plan, our annual profit and loss statement, and our most recent cash flow statement for your review. These financial documents and our strong credit score of 790 combine to make us a safe credit risk for Bank of American Businesses.

I would greatly appreciate the opportunity to speak with you about a small business loan. I can be reached at 983-744-6597 or by email at [email protected] .

Loan Request Letter Template

Writing a loan request letter takes a bit of time and research, but does not have to be difficult. Using the above format, you can easily request a loan for your small business or a personal need. The sample letter demonstrates how to make a great first impression on a lending institution.

How did our templates helped you today?

Opps what went wrong, related posts.

Boyfriend Application Forms

Rental Application Forms & Templates

Rental Application Denial Letter: Template and Example

Leave Application Cancellation Letter

Cancellation Letter for House Purchase – Sample & Template

Sample Application Cancellation Letter (Tips & Template)

How to Write a Maternity Leave Letter

Leave of Absence Letter for Personal Reasons

Thank you for your feedback.

Written Samples

15 sample letters of approval of loan.

Securing a loan, whether for personal or business purposes, can be a life-changing moment.

It begins a new chapter, filled with opportunities and possibilities. However, the path to loan approval is not always straightforward.

Lenders must carefully evaluate each application, assessing the borrower’s creditworthiness, financial stability, and loan repayment ability.

Sample Letters of Approval of Loan

When the stars align, and the loan is approved, the lender sends a letter of approval, officially confirming the good news.

In this article, we will explore 15 sample letters of loan approval, showcasing different scenarios and loan types. From mortgages to business loans, these letters will provide insight into the language and structure lenders use to convey their decisions.

Subject: Approval of Personal Loan – Application #12345

Dear Mr. Johnson,

We are pleased to inform you that your application for a personal loan has been approved. After careful consideration of your financial situation and creditworthiness, we have determined that you meet our lending criteria.

Loan Details: Loan Amount: $10,000 Interest Rate: 6.99% (Fixed) Loan Term: 36 months Monthly Payment: $305.00

To proceed with the loan, please review and sign the enclosed loan agreement. Once we receive the signed agreement, along with any additional required documentation, we will disburse the funds to your designated bank account within 3-5 business days.

If you have any questions or require further assistance, please don’t hesitate to contact our loan department at (123) 456-7890 or [email protected] .

Congratulations on your loan approval, and thank you for choosing ABC Bank for your financial needs.

Sarah Thompson

Loan Officer ABC Bank

Subject: Approval of Business Loan – Application #67890

Dear Ms. Patel,

We are delighted to inform you that your application for a business loan has been approved. After conducting a thorough evaluation of your business plan, financial statements, and creditworthiness, we are confident in your ability to repay the loan and achieve your business goals.

Loan Details: Loan Amount: $50,000 Interest Rate: 7.99% (Variable) Loan Term: 60 months Monthly Payment: $1,010.00

To move forward with the loan, please review and sign the enclosed loan agreement. Additionally, we require a copy of your business registration and any necessary collateral documentation. Once we receive these items, we will schedule a meeting with you to finalize the loan and discuss the disbursement of funds.

If you have any questions or need further clarification, please don’t hesitate to reach out to our business lending team at (123) 456-7890 or [email protected] .

Congratulations on this exciting milestone for your business. We look forward to working with you and supporting your success.

Best regards,

Michael Chen

Business Loan Officer XYZ Bank

Subject: Approval of Mortgage Loan – Application #24680

Dear Mr. and Mrs. Davis,

Congratulations! We are thrilled to inform you that your mortgage loan application has been approved. After carefully reviewing your financial information, employment history, and property details, we are pleased to offer you the following loan terms:

Loan Details: Loan Amount: $300,000 Interest Rate: 3.75% (Fixed) Loan Term: 30 years Monthly Payment: $1,389.00 (Principal and Interest)

To proceed with the loan, please review and sign the enclosed loan documents. We will also require proof of homeowners insurance and a copy of the property appraisal. Once we receive these items, we will schedule a closing date to finalize the loan and transfer the funds.

If you have any questions or need assistance throughout this process, our mortgage team is here to help. You can reach us at (123) 456-7890 or [email protected] .

We are excited to help you achieve your dream of homeownership and look forward to working with you.

Emily Nguyen

Mortgage Loan Officer ABC Bank

Subject: Approval of Auto Loan – Application #13579

Dear Ms. Rodriguez,

We are pleased to inform you that your application for an auto loan has been approved. Based on your credit history, income, and the vehicle information provided, we are happy to offer you the following loan terms:

Loan Details: Loan Amount: $25,000 Interest Rate: 4.99% (Fixed) Loan Term: 60 months Monthly Payment: $471.00

To accept this loan offer, please review and sign the enclosed loan agreement. Once we receive the signed agreement, along with proof of vehicle insurance and the dealership’s purchase order, we will disburse the funds directly to the dealership.

If you have any questions or need further assistance, our auto lending team is available at (123) 456-7890 or [email protected] .

Congratulations on your new vehicle purchase, and thank you for choosing XYZ Bank for your auto financing needs.

Auto Loan Officer XYZ Bank

Subject: Approval of Home Equity Loan – Application #97531

Dear Mr. Brown,

We are delighted to inform you that your application for a home equity loan has been approved. After evaluating your home’s equity, credit history, and financial situation, we are pleased to offer you the following loan terms:

Loan Details: Loan Amount: $50,000 Interest Rate: 5.99% (Fixed) Loan Term: 120 months Monthly Payment: $555.00

To proceed with the loan, please review and sign the enclosed loan documents. We will also require a copy of your home insurance policy and a recent property tax statement. Once we receive these items, we will schedule a closing date to finalize the loan and disburse the funds.

If you have any questions or need further clarification, our home equity lending team is here to help. You can reach us at (123) 456-7890 or [email protected] .

Congratulations on leveraging your home’s equity to achieve your financial goals. We look forward to working with you.

Jessica Patel

Home Equity Loan Officer ABC Bank

Subject: Approval of Student Loan – Application #86420

Dear Ms. Taylor,

We are pleased to inform you that your application for a student loan has been approved. After reviewing your enrollment status, academic records, and financial information, we are happy to offer you the following loan terms:

Loan Details: Loan Amount: $20,000 Interest Rate: 4.5% (Fixed) Loan Term: 120 months Grace Period: 6 months after graduation Monthly Payment: $207.00 (after the grace period)

To accept this loan offer, please review and sign the enclosed loan agreement and promissory note. Additionally, we require confirmation of your enrollment and a copy of your financial aid award letter. Once we receive these items, we will disburse the funds directly to your educational institution.

If you have any questions or need assistance throughout this process, our student lending team is available at (123) 456-7890 or [email protected] .

Congratulations on your academic pursuits, and thank you for choosing XYZ Bank to support your educational journey.

Student Loan Officer XYZ Bank

Subject: Approval of Small Business Loan – Application #24681

Dear Ms. Johnson,

We are delighted to inform you that your application for a small business loan has been approved. After conducting a thorough evaluation of your business plan, financial projections, and creditworthiness, we are confident in your ability to repay the loan and grow your business.

Loan Details: Loan Amount: $75,000 Interest Rate: 6.99% (Fixed) Loan Term: 84 months Monthly Payment: $1,092.00

To move forward with the loan, please review and sign the enclosed loan agreement. Additionally, we require a copy of your business license, articles of incorporation, and any necessary collateral documentation. Once we receive these items, we will schedule a meeting with you to finalize the loan and discuss the disbursement of funds.

If you have any questions or need further clarification, please don’t hesitate to reach out to our small business lending team at (123) 456-7890 or [email protected] .

Congratulations on this exciting milestone for your small business. We look forward to working with you and supporting your success.

Olivia Nguyen

Small Business Loan Officer ABC Bank

Subject: Approval of Debt Consolidation Loan – Application #13579

Dear Mr. Davis,

We are pleased to inform you that your application for a debt consolidation loan has been approved. After carefully reviewing your credit history, income, and existing debt obligations, we are happy to offer you the following loan terms:

Loan Details: Loan Amount: $30,000 Interest Rate: 7.99% (Fixed) Loan Term: 60 months Monthly Payment: $606.00

By consolidating your debts into a single loan with a lower interest rate, you can simplify your finances and potentially save money on interest charges over time.

To proceed with the loan, please review and sign the enclosed loan agreement. Once we receive the signed agreement, we will disburse the funds directly to your creditors as specified in the loan application.

If you have any questions or need further assistance, our loan consolidation team is available at (123) 456-7890 or [email protected] .

Congratulations on taking this important step towards financial freedom, and thank you for choosing XYZ Bank for your debt consolidation needs.

William Chen

Loan Consolidation Officer XYZ Bank

Subject: Approval of Personal Line of Credit – Application #86420

We are delighted to inform you that your application for a personal line of credit has been approved. After evaluating your credit history, income, and financial stability, we are pleased to offer you the following terms:

Line of Credit Details: Credit Limit: $15,000 Interest Rate: 9.99% (Variable) Annual Fee: None Minimum Payment: 2% of outstanding balance

A personal line of credit provides you with the flexibility to borrow funds as needed, up to your approved credit limit. You will only pay interest on the amount you borrow, and you can repay the funds at your own pace, subject to the minimum payment requirement.

To accept this offer, please review and sign the enclosed line of credit agreement. Once we receive the signed agreement, we will activate your account and provide you with access to the funds.

If you have any questions or need further clarification, our banking team is here to help. You can reach us at (123) 456-7890 or [email protected] .

Congratulations on your approved personal line of credit. We look forward to serving your financial needs and providing you with the flexibility you require.

Sophia Patel

Personal Banking Officer ABC Bank

Subject: Approval of Equipment Financing – Application #24681

We are pleased to inform you that your application for equipment financing has been approved. After carefully reviewing your business’s financial statements, credit history, and the equipment quotes provided, we are happy to offer you the following financing terms:

Financing Details: Equipment Cost: $100,000 Down Payment: $20,000 Financed Amount: $80,000 Interest Rate: 5.99% (Fixed) Loan Term: 60 months Monthly Payment: $1,509.00

By financing your equipment purchase, you can preserve your working capital and acquire the necessary tools to grow your business.

To proceed with the financing, please review and sign the enclosed financing agreement. Additionally, we require a copy of the equipment invoice and proof of insurance. Once we receive these items, we will disburse the funds directly to the equipment vendor.

If you have any questions or need further assistance, our equipment financing team is available at (123) 456-7890 or [email protected] .

Congratulations on this exciting investment in your business, and thank you for choosing XYZ Bank for your equipment financing needs.

Equipment Financing Officer XYZ Bank

Subject: Approval of Construction Loan – Application #13579

We are delighted to inform you that your application for a construction loan has been approved. After conducting a thorough evaluation of your building plans, cost estimates, and creditworthiness, we are confident in your ability to complete the construction project successfully.

Loan Details: Loan Amount: $500,000 Interest Rate: 4.99% (Fixed) Loan Term: 12 months (construction phase) + 30 years (permanent financing) Monthly Payment: $2,661.00 (during permanent financing)

To move forward with the loan, please review and sign the enclosed loan agreement. Additionally, we require a copy of the building permits, contractor agreements, and proof of insurance. Once we receive these items, we will schedule a meeting with you to finalize the loan and discuss the disbursement of funds.

If you have any questions or need further clarification, please don’t hesitate to reach out to our construction lending team at (123) 456-7890 or [email protected] .

Congratulations on this exciting milestone in your construction project. We look forward to working with you and seeing your vision come to life.

Construction Loan Officer ABC Bank

Subject: Approval of Accounts Receivable Financing – Application #86420

We are pleased to inform you that your application for accounts receivable financing has been approved. After carefully reviewing your business’s financial statements, accounts receivable aging report, and creditworthiness, we are happy to offer you the following financing terms:

Financing Details: Maximum Financing Amount: $200,000 Advance Rate: 80% of eligible accounts receivable Discount Fee: 2% per 30 days Reserve Amount: 20% of financed receivables

By leveraging your accounts receivable, you can improve your cash flow and access the working capital needed to grow your business.

To proceed with the financing, please review and sign the enclosed financing agreement. Additionally, we require a copy of your most recent accounts receivable aging report and a list of your customers. Once we receive these items, we will set up your account and begin funding your eligible invoices.

If you have any questions or need further assistance, our accounts receivable financing team is available at (123) 456-7890 or [email protected] .

Congratulations on this exciting opportunity to improve your business’s cash flow, and thank you for choosing XYZ Bank for your financing needs.

Liam Nguyen

Accounts Receivable Financing Officer XYZ Bank

Subject: Approval of Inventory Financing – Application #24681

Dear Ms. Davis,

We are delighted to inform you that your application for inventory financing has been approved. After conducting a thorough evaluation of your business’s financial statements, inventory turnover, and creditworthiness, we are confident in your ability to manage and sell the financed inventory effectively.

Financing Details: Maximum Financing Amount: $150,000 Advance Rate: 70% of eligible inventory Interest Rate: 6.99% (Fixed) Loan Term: 12 months Monthly Payment: $13,138.00

By financing your inventory purchases, you can free up working capital and ensure a steady supply of goods to meet customer demand.

To move forward with the financing, please review and sign the enclosed financing agreement. Additionally, we require a copy of your most recent inventory report and a list of your suppliers. Once we receive these items, we will schedule a meeting with you to finalize the financing and discuss the disbursement of funds.

If you have any questions or need further clarification, please don’t hesitate to reach out to our inventory financing team at (123) 456-7890 or [email protected] .

Congratulations on this exciting milestone for your business. We look forward to working with you and supporting your inventory management needs.

Inventory Financing Officer ABC Bank

Subject: Approval of Commercial Real Estate Loan – Application #13579

We are pleased to inform you that your application for a commercial real estate loan has been approved. After carefully reviewing the property details, income projections, and your creditworthiness, we are happy to offer you the following loan terms:

Loan Details: Loan Amount: $1,000,000 Interest Rate: 5.5% (Fixed) Loan Term: 25 years Monthly Payment: $6,135.00 Loan-to-Value Ratio: 70%

By investing in commercial real estate, you can build equity, generate rental income, and benefit from potential property appreciation.

To proceed with the loan, please review and sign the enclosed loan agreement. Additionally, we require a copy of the property appraisal, title report, and proof of insurance. Once we receive these items, we will schedule a closing date to finalize the loan and disburse the funds.

If you have any questions or need further assistance, our commercial real estate lending team is available at (123) 456-7890 or [email protected] .

Congratulations on this significant investment in your business’s future, and thank you for choosing XYZ Bank for your commercial real estate financing needs.

Commercial Real Estate Loan Officer XYZ Bank

Subject: Approval of SBA Loan – Application #86420

We are delighted to inform you that your application for a Small Business Administration (SBA) loan has been approved. After conducting a thorough evaluation of your business plan, financial projections, and creditworthiness, we are confident in your ability to repay the loan and achieve your business goals.

Loan Details: Loan Amount: $250,000 Interest Rate: 6.75% (Fixed) Loan Term: 10 years Monthly Payment: $2,853.00 SBA Guarantee: 75%

The SBA loan program provides favorable terms and conditions to help small businesses access the capital they need to grow and succeed.

To move forward with the loan, please review and sign the enclosed loan agreement. Additionally, we require a copy of your business license, articles of incorporation, and personal guarantees from all owners with a 20% or greater stake in the business. Once we receive these items, we will schedule a meeting with you to finalize the loan and discuss the disbursement of funds.

If you have any questions or need further clarification, please don’t hesitate to reach out to our SBA lending team at (123) 456-7890 or [email protected] .

SBA Loan Officer ABC Bank

Receiving a loan approval letter is a moment of celebration for borrowers. It signifies the lender’s confidence in their ability to repay the loan and marks the beginning of a new chapter in their financial journey.

For lenders, crafting effective loan approval letters is an essential part of the lending process, as these letters set the tone for the borrower-lender relationship and provide crucial information about the loan terms and conditions.

By exploring these 15 sample letters of loan approval, we have gained insight into the key elements that make a loan approval letter informative, professional, and impactful.

From clearly outlining the loan details to providing instructions for moving forward, these letters serve as a roadmap for borrowers as they embark on their financing journey.

Whether you are a borrower eagerly awaiting news of your loan application or a lender looking to refine your approval process, these sample letters offer valuable guidance and inspiration.

By tailoring these templates to your specific needs and borrower profiles, you can create loan approval letters that not only convey the necessary information but also foster a positive and productive relationship with your borrowers.

Remember, a well-crafted loan approval letter is more than just a formality; it is an opportunity to build trust, set expectations, and pave the way for a successful lending experience.

So, take the time to carefully consider the language, structure, and tone of your approval letters, and use these samples as a starting point to create your own effective and impactful communications.

All Formats

22+ Sample Loan Application Letters – PDF, DOC

There are times when we need financial aid to push through with our education, business ideas, or other personal projects or goals which require a huge amount of money for its realization. It is for this reason that lending companies have been existing ever since the days of old. Today, the primary step to being taken by someone who wants to borrow money from another individual or institution is to write a loan application letter .

Loan Application Letter

• Google Docs
• Apple Pages

Application for Loan Sample PDF

Simple Loan Application Letter

Application for Loan

Loan Letter Sample

Loan Request Letter

Letter for Loan Request

Formal Loan Purpose Application Letter to Senior Manager

Formal Event Management Small Business Letter

Sample Vehicle Application Letter Example

Agricultural Office Vehicle Application Letter Template

Sample Foreclosure Disbursement Application Form Letter

Example Work Travel Agency Letter

Application Letter to Canadian Bank for Loan

Sales Department Employee Application Letter Example

The Loan Application Process

• Before the loan contract , the borrower would send a loan application cover letter to the prospective lender to express his or her intent to ask for a loan.
• Afterward, when the lender has decided to consider the application for a loan made by the borrower, the borrower, and the lender would convene to negotiate the terms of the loan.
• The payment method, whether personal, through a check, online banking, etc.
• The number of times the payment is going to be made. There are various options. For example, the loan can be paid at one time, or it can be done in yearly or monthly installments.
• The amount of interest to be added on top of the loaned amount. The interest is the amount of money that is charged by the lender to the borrower on top of the amount which he/she has loaned. You may also see job reference letters .
• The assets (land, buildings, vehicles, or other properties) of the borrower would serve as collateral damage in case the borrower fails to make his/her payment on the time it is due.

Basic Senior Typist Home Loan Application Letter Template

Mortgage Loan Application Letter with Boss Recommendation

Professional Medical Loan Facility for Cancer Treatment

Professional Education Application Letter Template

Request Urgent / Emergency Loan Letter for Borrowing Money

Free Commercial Vehicle Application Letter Template

Loan Application Letter for Wedding/Marriage Template

Sample Staff Loan Request Application Letter for Covid-19

Things To Remember in Writing a Loan Application Letter

• Observe the proper rules for writing formal letters.
• State your intent to borrow a specific amount of money.
• Explain in detail the reason for borrowing money. You must be offering a clear, honest, and transparent explanation as to how you intend to utilize the money you intend to borrow. You may also see free application rejection letters .
• Enumerate your assets and liabilities.
• State the time, date, manner, and method which you prefer to make your payment.

More in Letters

Sample Loan Application Letter Template

Simple loan application letter template, loan application letter to employer template, personal loan application letter template, loan application letter for school fees template, loan application letter to bank manager template, loan application letter for house rent template, loan application letter from employee template, loan application request letter to boss template, office loan application letter template.

• FREE 26+ Covid-19 Letter Templates in PDF | MS Word | Google Docs
• Thank You Letter for Appreciation – 19+ Free Word, Excel, PDF Format Download!
• 69+ Resignation Letter Templates – Word, PDF, IPages
• 12+ Letter of Introduction Templates – PDF, DOC
• 14+ Nurse Resignation Letter Templates – Word, PDF
• 16+ Sample Adoption Reference Letter Templates
• 10+ Sample Work Reference Letters
• 28+ Invitation Letter Templates
• 19+ Rental Termination Letter Templates – Free Sample, Example Format Download!
• 23+ Retirement Letter Templates – Word, PDF
• 12+ Thank You Letters for Your Service – PDF, DOC
• 12+ Job Appointment Letter Templates – Google DOC, PDF, Apple Pages
• 21+ Professional Resignation Letter Templates – PDF, DOC
• 14+ Training Acknowledgement Letter Templates
• 49+ Job Application Form Templates

File Formats

Word templates, google docs templates, excel templates, powerpoint templates, google sheets templates, google slides templates, pdf templates, publisher templates, psd templates, indesign templates, illustrator templates, pages templates, keynote templates, numbers templates, outlook templates.

• Add New post Add New reply

Login Or Register

Revised d.a. in uttarakhand from 1st april-2023

Revised da april 2023.pdf

Interest Tags

Trending tags, request for loan from provident fund account.

Reason for vote

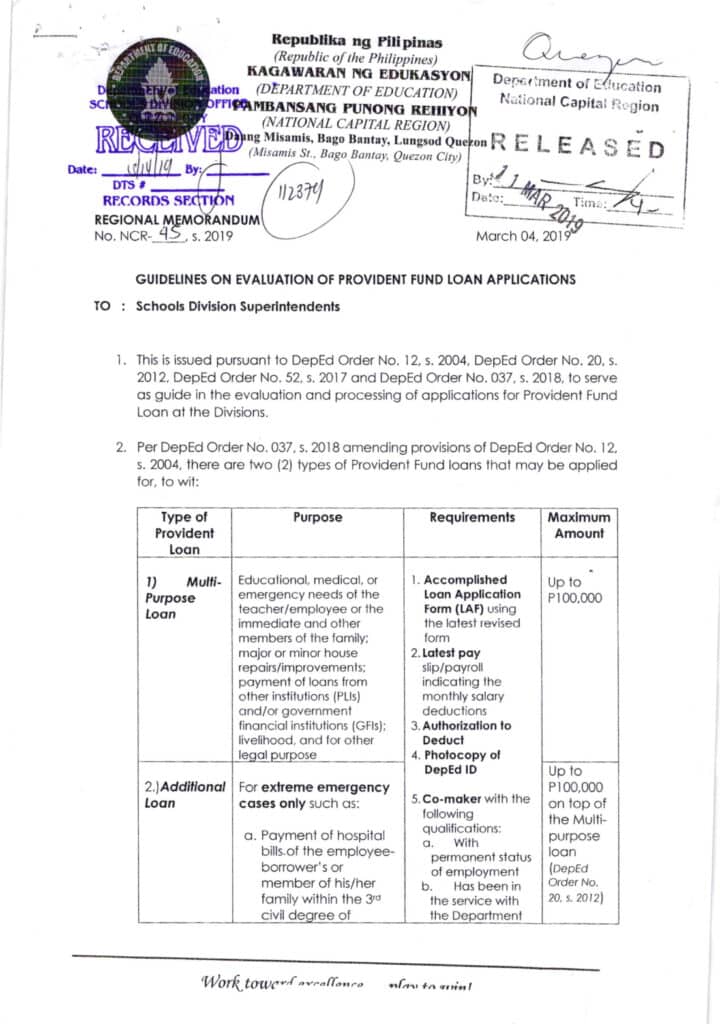
2019 DepEd Guidelines on Evaluation of Provident Fund Loan Applications

Pursuant to DepEd Order No. 12, s. 2004, DepEd Order No. 20, s. 2012, DepEd Order No. 52, s. 2017 and DepEd Order No. 037, s. 2018, enclosed is Regional Memorandum No. NCR-45. S. 2019, from Dr. Wilfredo E. Cabral, Officer In-Charge, Office of the Regional Director, DepEd-NCR, dated March 4, 2019, relative to the “Guidelines On Evaluation Of Provident Fund Loan Applications” , which is self-explanatory, for the information and guidance of all concerned.

Attention is invited to item nos. 1 to 8 of the said Memorandum.

Table of Contents

Guidelines on Evaluation of Provident Fund Loan Applications

This is issued pursuant to DepEd Order No. 12, s. 2004, DepEd Order No. 20, s. 2012, DepEd Order No. 52, s. 2017 and DepEd Order No. 037, s. 2018, to serve as guide in the evaluation and processing of applications for Provident Fund Loan at the Divisions.

Per DepEd Order No. 037, s. 2018 amending provisions of DepEd Order No. 12, s. 2004, there are two (2) types of Provident Fund loans that may be applied for, to wit:

Per Regional Board of Trustees Resolution No. 001, s. 2019, the approval of Multipurpose Loan is delegated to the Division Superintendent, subject to evaluation by the Division Secretariat whose members are designated in Regional Memorandum No. 26, s. 2019 dated February 4, 2019 as follows:

• Administrative Officer (Administrative Section)
• Legal Officer/Attorney III

As stated in par no. 1 of DepEd Order No. 037, s. 2018, applications for Additional Loan at the Regional and Schools Division Provident Fund Chapters shall be approved by the PF Regional Board of Trustees . However, the Division Secretariat. For this purpose, the School Division Superintendent shall serve as head of the Secretariat per Regional Memorandum No. 26, s. 2019, who shall recommend approval in the prescribed Form. The Division Secretariat shall evaluate the application if it falls under Additional Loan and recommend for approval of the Regional Board. If the purpose of the Additional Loan does not meet the conditions, the Division Secretariat shall immediately disapprove the loan request and notify the concerned teacher/employee-borrower .

All Provident Fund loan applications in the Division shall evaluated by the Division Secretariat and accomplish the Revised Form accordingly. As to Additional Loan application , the head of the Division Secretariat shall recommend for approval to the Chairperson of the Regional Provident Fund Board.

The Division render monthly/quarterly reports to the Regional Board on the status of operations and financial condition of the Fund.

All applications shall be subject to the capacity to pay of the employee borrower and the prescribed net take home pay.

The interest rate for Provident Fund loan is 6% per annum , with no grace period on the start of payment of loan, computed using the diminishing/declining balance method.

Newly hired teachers are allowed to avail of Provident Fund loan equivalent to his/her one month basic salary, payable in 6 months, on the same rate of interest, diminishing balance method (par. 2 of DepEd Order No. 037, s. 2018).

Renewal of Provident Fund loan may be allowed provided that:

a) 30% of the existing loan has been paid;

b) there are no pending applications for new loans, and

c) the balance of the principal amount shall be deducted from the new loan.

For information and compliance.

DepEd NCR Regional Memorandum No. 45, s. 2019

Mark Anthony Llego

Mark Anthony Llego, hailing from the Philippines, has made a profound impact on the teaching profession by enabling thousands of teachers nationwide to access crucial information and engage in meaningful exchanges of ideas. His contributions have significantly enhanced their instructional and supervisory capabilities, elevating the quality of education in the Philippines. Beyond his domestic influence, Mark's insightful articles on teaching have garnered international recognition, being featured on highly respected educational websites in the United States. As an agent of change, he continues to empower teachers, both locally and internationally, to excel in their roles and make a lasting difference in the lives of their students, serving as a shining example of the transformative power of knowledge-sharing and collaboration within the teaching community.

Leave a Comment Cancel reply

Can't find what you're looking for.

We are here to help - please use the search box below.