Operations Research
191. The large negative opportunity cost value in an unused cell in a transportation table is chosen to improve the current solution because
- It represents per unit cost reduction
- It represents per unit cost improvement
- It ensure no rim requirement violation
- None of the above
Correct answer: (A) It represents per unit cost reduction
192. The method of finding an initial solution based upon opportunity costs is called __________.
- the northwest corner rule
- Vogel's approximation
- Johanson's theorem
- Flood's technique
- Hungarian method
Correct answer: (B) Vogel's approximation
193. The net cost of shipping one unit on a route not used in the current transportation problem solution is called the __________.
- change index
- Improvement index
Correct answer: (E) Improvement index
194. The objective function and constraints are functions of two types of variables, __________ variables and __________ variables.
- Positive and negative
- Controllable and uncontrollable
- Strong and weak
Correct answer: (B) Controllable and uncontrollable
195. The objective function for a minimization problem is given by z = 2 x1 - 5 x2 + 3 x3 The hyperplane for the objective function cuts a bounded feasible region in the space (x1,x2,x3). Find the direction vector d, where a finite optimal solution can be reached.
- d(-2,-5,-3)
Correct answer: (B) d(-2,5,-3)
196. The occurrence of degeneracy while solving a transportation problem means that
- Total supply equals total demand
- The solution so obtained is not feasible
- The few allocations become negative
Correct answer: (B) The solution so obtained is not feasible
197. The only restriction we place on the initial solution of a transportation problem is that: we must have nonzero quantities in a majority of the boxes.
- all constraints must be satisfied.
- demand must equal supply.
- we must have a number (equal to the number of rows plus the number of columns minus one) of boxes which contain nonzero quantities.
Correct answer: (A) all constraints must be satisfied.
198. The Operations research technique which helps in minimizing total waiting and service costs is
- Queuing Theory
- Decision Theory
- Both A and B
Correct answer: (A) Queuing Theory
199. The procedure used to solve assignment problems wherein one reduces the original assignment costs to a table of opportunity costs is called __________.
- stepping-stone method
- matrix reduction
- MODI method
- northwest reduction
- simplex reduction
Correct answer: (B) matrix reduction
200. The purpose of a dummy source or dummy destination in a transportation problem is to
- prevent the solution from becoming degenerate.
- obtain a balance between total supply and total demand.
- make certain that the total cost does not exceed some specified figure.
- provide a means of representing a dummy problem.
Correct answer: (B) obtain a balance between total supply and total demand.

Search MBA MCQ.com

How to Solve the Assignment Problem: A Complete Guide
Table of Contents
Assignment problem is a special type of linear programming problem that deals with assigning a number of resources to an equal number of tasks in the most efficient way. The goal is to minimize the total cost of assignments while ensuring that each task is assigned to only one resource and each resource is assigned to only one task. In this blog, we will discuss the solution of the assignment problem using the Hungarian method, which is a popular algorithm for solving the problem.
Understanding the Assignment Problem
Before we dive into the solution, it is important to understand the problem itself. In the assignment problem, we have a matrix of costs, where each row represents a resource and each column represents a task. The objective is to assign each resource to a task in such a way that the total cost of assignments is minimized. However, there are certain constraints that need to be satisfied – each resource can be assigned to only one task and each task can be assigned to only one resource.
Solving the Assignment Problem
There are various methods for solving the assignment problem, including the Hungarian method, the brute force method, and the auction algorithm. Here, we will focus on the steps involved in solving the assignment problem using the Hungarian method, which is the most commonly used and efficient method.
Step 1: Set up the cost matrix
The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.
Step 2: Subtract the smallest element from each row and column
To simplify the calculations, we need to reduce the size of the cost matrix by subtracting the smallest element from each row and column. This step is called matrix reduction.
Step 3: Cover all zeros with the minimum number of lines
The next step is to cover all zeros in the matrix with the minimum number of horizontal and vertical lines. This step is called matrix covering.
Step 4: Test for optimality and adjust the matrix
To test for optimality, we need to calculate the minimum number of lines required to cover all zeros in the matrix. If the number of lines equals the number of rows or columns, the solution is optimal. If not, we need to adjust the matrix and repeat steps 3 and 4 until we get an optimal solution.
Step 5: Assign the tasks to the agents
The final step is to assign the tasks to the agents based on the optimal solution obtained in step 4. This will give us the most cost-effective or profit-maximizing assignment.
Solution of the Assignment Problem using the Hungarian Method
The Hungarian method is an algorithm that uses a step-by-step approach to find the optimal assignment. The algorithm consists of the following steps:
- Subtract the smallest entry in each row from all the entries of the row.
- Subtract the smallest entry in each column from all the entries of the column.
- Draw the minimum number of lines to cover all zeros in the matrix. If the number of lines drawn is equal to the number of rows, we have an optimal solution. If not, go to step 4.
- Determine the smallest entry not covered by any line. Subtract it from all uncovered entries and add it to all entries covered by two lines. Go to step 3.
The above steps are repeated until an optimal solution is obtained. The optimal solution will have all zeros covered by the minimum number of lines. The assignments can be made by selecting the rows and columns with a single zero in the final matrix.
Applications of the Assignment Problem
The assignment problem has various applications in different fields, including computer science, economics, logistics, and management. In this section, we will provide some examples of how the assignment problem is used in real-life situations.
Applications in Computer Science
The assignment problem can be used in computer science to allocate resources to different tasks, such as allocating memory to processes or assigning threads to processors.
Applications in Economics
The assignment problem can be used in economics to allocate resources to different agents, such as allocating workers to jobs or assigning projects to contractors.
Applications in Logistics
The assignment problem can be used in logistics to allocate resources to different activities, such as allocating vehicles to routes or assigning warehouses to customers.
Applications in Management
The assignment problem can be used in management to allocate resources to different projects, such as allocating employees to tasks or assigning budgets to departments.
Let’s consider the following scenario: a manager needs to assign three employees to three different tasks. Each employee has different skills, and each task requires specific skills. The manager wants to minimize the total time it takes to complete all the tasks. The skills and the time required for each task are given in the table below:
| Task 1 | Task 2 | Task 3 | |
|---|---|---|---|
| Emp 1 | 5 | 7 | 6 |
| Emp 2 | 6 | 4 | 5 |
| Emp 3 | 8 | 5 | 3 |
The assignment problem is to determine which employee should be assigned to which task to minimize the total time required. To solve this problem, we can use the Hungarian method, which we discussed in the previous blog.
Using the Hungarian method, we first subtract the smallest entry in each row from all the entries of the row:
| Task 1 | Task 2 | Task 3 | |
|---|---|---|---|
| Emp 1 | 0 | 2 | 1 |
| Emp 2 | 2 | 0 | 1 |
| Emp 3 | 5 | 2 | 0 |
Next, we subtract the smallest entry in each column from all the entries of the column:
| Task 1 | Task 2 | Task 3 | |
|---|---|---|---|
| Emp 1 | 0 | 2 | 1 |
| Emp 2 | 2 | 0 | 1 |
| Emp 3 | 5 | 2 | 0 |
| 0 | 0 | 0 |
We draw the minimum number of lines to cover all the zeros in the matrix, which in this case is three:
Since the number of lines is equal to the number of rows, we have an optimal solution. The assignments can be made by selecting the rows and columns with a single zero in the final matrix. In this case, the optimal assignments are:
- Emp 1 to Task 3
- Emp 2 to Task 2
- Emp 3 to Task 1
This assignment results in a total time of 9 units.
I hope this example helps you better understand the assignment problem and how to solve it using the Hungarian method.
Solving the assignment problem may seem daunting, but with the right approach, it can be a straightforward process. By following the steps outlined in this guide, you can confidently tackle any assignment problem that comes your way.
How useful was this post?
Click on a star to rate it!
Average rating 0 / 5. Vote count: 0
No votes so far! Be the first to rate this post.
We are sorry that this post was not useful for you! 😔
Let us improve this post!
Tell us how we can improve this post?
Operations Research
1 Operations Research-An Overview
- History of O.R.
- Approach, Techniques and Tools
- Phases and Processes of O.R. Study
- Typical Applications of O.R
- Limitations of Operations Research
- Models in Operations Research
- O.R. in real world
2 Linear Programming: Formulation and Graphical Method
- General formulation of Linear Programming Problem
- Optimisation Models
- Basics of Graphic Method
- Important steps to draw graph
- Multiple, Unbounded Solution and Infeasible Problems
- Solving Linear Programming Graphically Using Computer
- Application of Linear Programming in Business and Industry
3 Linear Programming-Simplex Method
- Principle of Simplex Method
- Computational aspect of Simplex Method
- Simplex Method with several Decision Variables
- Two Phase and M-method
- Multiple Solution, Unbounded Solution and Infeasible Problem
- Sensitivity Analysis
- Dual Linear Programming Problem
4 Transportation Problem
- Basic Feasible Solution of a Transportation Problem
- Modified Distribution Method
- Stepping Stone Method
- Unbalanced Transportation Problem
- Degenerate Transportation Problem
- Transhipment Problem
- Maximisation in a Transportation Problem
5 Assignment Problem
- Solution of the Assignment Problem
- Unbalanced Assignment Problem
- Problem with some Infeasible Assignments
- Maximisation in an Assignment Problem
- Crew Assignment Problem
6 Application of Excel Solver to Solve LPP
- Building Excel model for solving LP: An Illustrative Example
7 Goal Programming
- Concepts of goal programming
- Goal programming model formulation
- Graphical method of goal programming
- The simplex method of goal programming
- Using Excel Solver to Solve Goal Programming Models
- Application areas of goal programming
8 Integer Programming
- Some Integer Programming Formulation Techniques
- Binary Representation of General Integer Variables
- Unimodularity
- Cutting Plane Method
- Branch and Bound Method
- Solver Solution
9 Dynamic Programming
- Dynamic Programming Methodology: An Example
- Definitions and Notations
- Dynamic Programming Applications
10 Non-Linear Programming
- Solution of a Non-linear Programming Problem
- Convex and Concave Functions
- Kuhn-Tucker Conditions for Constrained Optimisation
- Quadratic Programming
- Separable Programming
- NLP Models with Solver
11 Introduction to game theory and its Applications
- Important terms in Game Theory
- Saddle points
- Mixed strategies: Games without saddle points
- 2 x n games
- Exploiting an opponent’s mistakes
12 Monte Carlo Simulation
- Reasons for using simulation
- Monte Carlo simulation
- Limitations of simulation
- Steps in the simulation process
- Some practical applications of simulation
- Two typical examples of hand-computed simulation
- Computer simulation
13 Queueing Models
- Characteristics of a queueing model
- Notations and Symbols
- Statistical methods in queueing
- The M/M/I System
- The M/M/C System
- The M/Ek/I System
- Decision problems in queueing
- Mathematical Sciences
Ones assignment method for solving assignment problems
- January 2012

- Shahid Chamran University of Ahvaz
Discover the world's research
- 25+ million members
- 160+ million publication pages
- 2.3+ billion citations
- R. Murugesan
- S. Thamarai Selvi
- T. ESAKKIAMMAL

- Research Scholar

- Tanuja S Dhope
- J. Boopalan

- Hamdy A. Taha
- J OPER RES SOC

- John J. Jarvis
- Shayle R. Searle

- Tapadar Rudrajit
- Recruit researchers
- Join for free
- Login Email Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google Welcome back! Please log in. Email · Hint Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google No account? Sign up
Algorithms: The Assignment Problem
One of the interesting things about studying optimization is that the techniques show up in a lot of different areas. The “assignment problem” is one that can be solved using simple techniques, at least for small problem sizes, and is easy to see how it could be applied to the real world.
Assignment Problem
Pretend for a moment that you are writing software for a famous ride sharing application. In a crowded environment, you might have multiple prospective customers that are requesting service at the same time, and nearby you have multiple drivers that can take them where they need to go. You want to assign the drivers to the customers in a way that minimizes customer wait time (so you keep the customers happy) and driver empty time (so you keep the drivers happy).
The assignment problem is designed for exactly this purpose. We start with m agents and n tasks. We make the rule that every agent has to be assigned to a task. For each agent-task pair, we figure out a cost associated to have that agent perform that task. We then figure out which assignment of agents to tasks minimizes the total cost.
Of course, it may be true that m != n , but that’s OK. If there are too many tasks, we can make up a “dummy” agent that is more expensive than any of the others. This will ensure that the least desirable task will be left to the dummy agent, and we can remove that from the solution. Or, if there are too many agents, we can make up a “dummy” task that is free for any agent. This will ensure that the agent with the highest true cost will get the dummy task, and will be idle.
If that last paragraph was a little dense, don’t worry; there’s an example coming that will help show how it works.
There are special algorithms for solving assignment problems, but one thing that’s nice about them is that a general-purpose solver can handle them too. Below is an example, but first it will help to cover a few concepts that we’ll be using.
Optimization Problems
Up above, we talked about making “rules” and minimizing costs. The usual name for this is optimization. An optimization problem is one where we have an “objective function” (which tells us what our goals are) and one or more “constraint functions” (which tell us what the rules are). The classic example is a factory that can make both “widgets” and “gadgets”. Each “widget” and “gadget” earns a certain amount of profit, but it also uses up raw material and time on the factory’s machines. The optimization problem is to determine exactly how many “widgets” and how many “gadgets” to make to maximize profit (the objective) while fitting within the material and time available (the constraints).
If we were to write this simple optimization problem out, it might look like this:
In this case, we have two variables: g for the number of gadgets we make and w for the number of widgets we make. We also have three constraints that we have to meet. Note that they are inequalities; we might not use all the available material or time in our optimal solution.
Just to unpack this a little: in English, the above is saying that we make 45 dollars / euros / quatloos per gadget we make. However, to make a gadget needs 120 lbs of raw material 1, 80 lbs of raw material 2, and 3.8 hours of machine time. So there is a limit on how many gadgets we can make, and it might be a better use of resources to balance gadgets with widgets.
Of course, real optimization problems have many more than two variables and many constraint functions, making them much harder to solve. The easiest kind of optimization problem to solve is linear, and fortunately, the assignment problem is linear.
Linear Programming
A linear program is a kind of optimization problem where both the objective function and the constraint functions are linear. (OK, that definition was a little self-referential.) We can have as many variables as we want, and as many constraint functions as we want, but none of the variables can have exponents in any of the functions. This limitation allows us to apply very efficient mathematical approaches to solve the problem, even for very large problems.
We can state the assignment problem as a linear programming problem. First, we choose to make “i” represent each of our agents (drivers) and “j” to represent each of our tasks (customers). Now, to write a problem like this, we need variables. The best approach is to use “indicator” variables, where xij = 1 means “driver i picks up customer j” and xij = 0 means “driver i does not pick up customer j”.
We wind up with:
This is a compact mathematical way to describe the problem, so again let me put it in English.
First, we need to figure out the cost of having each driver pick up each customer. Then, we can calculate the total cost for any scenario by just adding up the costs for the assignments we pick. For any assignment we don’t pick, xij will equal zero, so that term will just drop out of the sum.
Of course, the way we set up the objective function, the cheapest solution is for no drivers to pick up any customers. That’s not a very good business model. So we need a constraint to show that we want to have a driver assigned to every customer. At the same time, we can’t have a driver assigned to mutiple customers. So we need a constraint for that too. That leads us to the two constraints in the problem. The first just says, if you add up all the assignments for a given driver, you want the total number of assignments for that driver to be exactly one. The second constraint says, if you add up all the assignments to a given customer, you want the total number of drivers assigned to the customer to be one. If you have both of these, then each driver is assigned to exactly one customer, and the customers and drivers are happy. If you do it in a way that minimizes costs, then the business is happy too.
Solving with Octave and GLPK
The GNU Linear Programming Kit is a library that solves exactly these kinds of problems. It’s easy to set up the objective and constraints using GNU Octave and pass these over to GLPK for a solution.
Given some made-up sample data, the program looks like this:
Start with the definition of “c”, the cost information. For this example, I chose to have four drivers and three customers. There are sixteen numbers there; the first four are the cost of each driver to get the first customer, the next four are for the second customer, and the next four are for the third customer. Because we have an extra driver, we add a “dummy” customer at the end that is zero cost. This represents one of the drivers being idle.
The next definition is “b”, the right-hand side of our constraints. There are eight constraints, one for each of the drivers, and one for each of the customers (including the dummy). For each constraint, the right-hand side is 1.
The big block in the middle defines our constraint matrix “a”. This is the most challenging part of taking the mathematical definition and putting it into a form that is usable by GLPK; we have to expand out each constraint. Fortunately, in these kinds of cases, we tend to get pretty patterns that help us know we’re on the right track.
The first line in “a” says that the first customer needs a driver. To see why, remember that in our cost information, the first four numbers are the cost for each driver to get the first customer. With this constraint, we are requiring that one of those four costs be included and therefore that a driver is “selected” for the first customer. The other lines in “a” work similarly; the last four ensure that each driver has an assignment.
Note that the number of rows in “a” matches the number of items in “b”, and the number of columns in “a” matches the number of items in “c”. This is important; GLPK won’t run if this is not true (and our problem isn’t stated right in any case).
Compared to the above, the last few lines are easy.
- “lb” gives the lower bound for each variable.
- “ub” gives the upper bound.
- “ctype” tells GLPK that each constraint is an equality (“strict” as opposed to providing a lower or upper bound).
- “vartype” tells GLPK that these variables are all integers (can’t have half a driver showing up).
- “s” tells GLPK that we want to minimize our costs, not maximize them.
We push all that through a function call to GLPK, and what comes back are two values (along with some other stuff I’ll exclude for clarity):
The first item tells us that our best solution takes 27 minutes, or dollars, or whatever unit we used for cost. The second item tells us the assignments we got. (Note for pedants: I transposed this output to save space.)
This output tells us that customer 1 gets driver 2, customer 2 gets driver 3, customer 3 gets driver 4, and driver 1 is idle. If you look back at the cost data, you can see this makes sense, because driver 1 had some of the most expensive times to the three customers. You can also see that it managed to pick the least expensive pairing for each customer. (Of course, if I had done a better job making up cost data, it might not have picked the least expensive pairing in all cases, because a suboptimal individual pairing might still lead to an overall optimal solution. But this is a toy example.)
Of course, for a real application, we would have to take into consideration many other factors, such as the passage of time. Rather than knowing all of our customers and drivers up front, we would have customers and drivers continually showing up and being assigned. But I hope this simple example has revealed some of the concepts behind optimization and linear programming and the kinds of real-world problems that can be solved.
Operations Research by P. Mariappan
Get full access to Operations Research and 60K+ other titles, with a free 10-day trial of O'Reilly.
There are also live events, courses curated by job role, and more.
Assignment Problem
5.1 introduction.
The assignment problem is one of the special type of transportation problem for which more efficient (less-time consuming) solution method has been devised by KUHN (1956) and FLOOD (1956). The justification of the steps leading to the solution is based on theorems proved by Hungarian mathematicians KONEIG (1950) and EGERVARY (1953), hence the method is named Hungarian.
5.2 GENERAL MODEL OF THE ASSIGNMENT PROBLEM
Consider n jobs and n persons. Assume that each job can be done only by one person and the time a person required for completing the i th job (i = 1,2,...n) by the j th person (j = 1,2,...n) is denoted by a real number C ij . On the whole this model deals with the assignment of n candidates to n jobs ...
Get Operations Research now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
Don’t leave empty-handed
Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.
It’s yours, free.

Check it out now on O’Reilly
Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

Assignment Problem: Meaning, Methods and Variations | Operations Research
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.
Meaning of Assignment Problem:
An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.
The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.
Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.
Definition of Assignment Problem:
ADVERTISEMENTS:
Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.
The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:
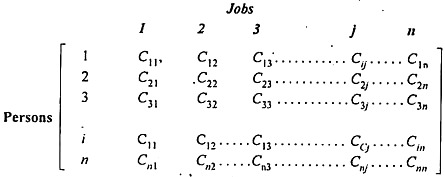

Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)
- For each row of the matrix, find the smallest element and subtract it from every element in its row.
- Do the same (as step 1) for all columns.
- Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
- Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
- Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.
Try it before moving to see the solution
Explanation for above simple example:
An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.
Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).
Space complexity : O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.
In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY
Please Login to comment...
Similar reads.
- Mathematical
Improve your Coding Skills with Practice
What kind of Experience do you want to share?

- Google OR-Tools
- Español – América Latina
- Português – Brasil
- Tiếng Việt
Solving an Assignment Problem
This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.
In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview .
The costs of assigning workers to tasks are shown in the following table.
| Worker | Task 0 | Task 1 | Task 2 | Task 3 |
|---|---|---|---|---|
| 90 | 80 | 75 | 70 | |
| 35 | 85 | 55 | 65 | |
| 125 | 95 | 90 | 95 | |
| 45 | 110 | 95 | 115 | |
| 50 | 100 | 90 | 100 |
The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task.
MIP solution
The following sections describe how to solve the problem using the MPSolver wrapper .
Import the libraries
The following code imports the required libraries.
Create the data
The following code creates the data for the problem.
The costs array corresponds to the table of costs for assigning workers to tasks, shown above.
Declare the MIP solver
The following code declares the MIP solver.
Create the variables
The following code creates binary integer variables for the problem.
Create the constraints
Create the objective function.
The following code creates the objective function for the problem.
The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.
Invoke the solver
The following code invokes the solver.
Print the solution
The following code prints the solution to the problem.
Here is the output of the program.
Complete programs
Here are the complete programs for the MIP solution.
CP SAT solution
The following sections describe how to solve the problem using the CP-SAT solver.
Declare the model
The following code declares the CP-SAT model.
The following code sets up the data for the problem.
The following code creates the constraints for the problem.
Here are the complete programs for the CP-SAT solution.
Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.
Last updated 2023-01-02 UTC.
- High School
the procedure used to solve assignment problems wherein one reduces the original assignment costs to a table of opportunity costs is called
Jorgepickens7130 is waiting for your help., ai-generated answer.
- 10K answers
- 2.3M people helped
The Hungarian method is used to solve assignment problems by transforming assignment costs into opportunity costs, facilitating the search for cost-effective solutions. Opportunity costs represent the value of the next best alternative given up when making a choice, and it is integral in economic decision-making, including the law of increasing opportunity costs.
The procedure used to solve assignment problems by reducing the original assignment costs to a table of opportunity costs is commonly referred to as the Hungarian method or the reduced cost method. The Hungarian method simplifies an assignment problem by converting all the potential costs into opportunity costs, thereby making it easier to identify the most cost-effective solution. This is done by subtracting the smallest element of each row and each column from other elements in the same row and column. This technique ensures that at least one zero exists in each row and column and allows for optimal assignment without affecting the overall cost.
Opportunity costs are an essential concept in economics that involve the examination of alternatives. It is the value of the best alternative foregone in a situation where a choice needs to be made. Moreover, the law of increasing opportunity cost is an economic principle that illustrates that as more of a good or service is produced, the opportunity cost of producing each additional unit is increased because resources are not equally efficient in producing all goods.
Understanding opportunity costs is crucial for making informed economic decisions, whether in business settings or in assigning tasks and resources more broadly. It encourages the examination of marginal gains against sacrifices made, which is a fundamental aspect of economic decision-making.
Still have questions?
Get more answers for free, you might be interested in, new questions in business.
Academia.edu no longer supports Internet Explorer.
To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to upgrade your browser .
Enter the email address you signed up with and we'll email you a reset link.
- We're Hiring!
- Help Center

REVISED ONES ASSIGNMENT METHOD FOR SOLVING ASSIGNMENT PROBLEM

The assignment problem (AP) is a special case of the transportation problem, in which the objective is to assign a number of re- sources to the equal number of activities at a minimum cost (or maximum profit). It has great significance subject discussed in real physical world for e.g. production planning, particular job tasks, economic etc. We endeavor in this paper to introduce a new approach to assignment problem namely “Revised Ones Assignment Method (ROA)” for solving wide range of problem. In ROA method first we define assignment matrix, then reduced matrix till it has at least one in each row and column. The new method is based on creating some ones in the assignment matrix and to complete exact assignment to their ones, we have added new step to ROA algorithm can be utilized for all types of AP with maximize or minimize objective functions and at last we have illustrate some numerical exam- ples.
Related Papers
Hogpodrat Pangkum
Assignment problem is a special case of Transportation problem. It is actually a minimizing model that assigns numbers of people with equal number of jobs, henceforth, minimizing the corresponding costs. In this paper an introduction is given to " New Improved Ones Assignment " which is a path to making an assignment problem. Earlier H. Gamel also brought to light the drawbacks of One assignment method. Our improvement to the Ones assignment method, leads to comparatively brief computation time and more convenient and strong codes. It also overcomes the drawbacks as mentioned previously
Trisna Darmawansyah
Assignment problem is an important subject discussed in real physical world. We endeavor in this paper to introduce a new approach to assignment problem namely, ones assignment method, for solving a wide rang of such problems. This method offers significant advantages over similar methods, in the process, first we define the assignment matrix, then by using determinant representation we obtain a reduced matrix which has at least one 1 in each row and columns. Then by using the new method, we obtain an optimal solution for assignment problem by assigning ones to each row and each column. The new method is based on creating some ones in the assignment matrix and then try to find a complete assignment to there ones. The proposed method is a systematic procedure, easy to apply and can be utilized for all types of assignment problem with maximize or minimize objective functions. At the end, this method is illustrated with some numerical examples.
Assignment problems arise in different situation where we have to find an optimal way to assign n-objects to mother objects in an injective fashion. The assignment problems are a well studied topic in combinatorial optimization. These problems find numerous application in production planning, telecommunication VLSI design, economic etc. The assignment problems is a special case of Transportation problem. Depending on the objective we want to optimize, we obtain the typical assignment problems. Assignment problem is an important subject discussed in real physical world we endeavor in this paper to introduce a new approach to assignment problem namely, matrix ones assignment method or MOA-method for solving wide range of problem. An example using matrix ones assignment methods and the existing Hungarian method have been solved and compared it graphically. Also some of the variations and some special cases in assignment problem and its applications have been discussed in the paper.
1 í µí°·í µí±í µí±í µí±í µí±í µí±¡í µí±í µí±í µí±í µí±¡í µí±í µí±í µí±í µí±í µí±¡ í µí±í µí±í µí±í µí±í µí±¡í µí±í µí±í µí± ,í µí° ¶í µí±í µí±í µí±í µí±í µí±í µí±í µí±í µí±í µí±í µí±£í µí±í µí±í µí± í µí±í µí±¡í µí±¦ ,í µí°µí µí±í µí±í µí±í µí±í µí±í µí±í µí±í µí± í µí± 2 í µí°·í µí±í µí±í µí±í µí±í µí±¡í µí±í µí±í µí±í µí±¡í µí±í µí±í µí±í µí±í µí±¡ í µí±í µí±í µí±í µí±í µí±¡í µí±í µí±í µí± ,í µí° ¶í µí±í µí±í µí±í µí±í µí±í µí±í µí±í µí±í µí±í µí±£í µí±í µí±í µí± í µí±í µí±¡í µí±¦ ,í µí°µí µí±í µí±í µí±í µí±í µí±í µí±í µí±í µí± í µí± Abstract: Assignment problem is an important problem in mathematics and is also discuss in real physical world. In this paper we attempt to introduce a new proposed approach for solving assignment problem with algorithm and solution steps. We examine a numerical example by using new method and compute by existing two methods. Also we compare the optimal solutions among this new method and two existing method .The proposed method isa systematic procedure, easy to apply for solving assignment problem.
IAEME Publication
Generalized Assignment Problem is a very popular topic which is used to solve different engineering and management problems. It becomes more realistic when used under fuzzy environment since in practical situation it is difficult to get precise data. In this paper cost for assigning the j-th job to the i-th person is taken as trapezoidal fuzzy numbers (TrFNs) which are more realistic and general in nature. To solve the real life problems restrictions have been put on both job cost and person cost depending on his/her efficiency/qualification. Yager’s Ranking Method[1] has been used for ranking the fuzzy numbers. The fuzzy generalized assignment problem (FGAP) has been solved by Modified Extremum Difference Method (EDM) for initial Basic Feasible Solution (BFS). To test the optimality MODI method is used. Again the solution by the proposed method has been verified by LINGO 9.0
IJAR Indexing
Assignment problems deal with the question how to assign n objects to m other objects in an injective fashion in the best possible way. An assignment problem is completely specified by its two components the assignments, which represent the underlying combinatorial structure, and the objective function to be optimized, which models \\\\\\\"the best possible way\\\\\\\". The assignment problem refers to another special class of linear programming problem where the objective is to assign a number of resources to an equal number of activities on a one to one basis so as to minimize total costs of performing the tasks at hand or maximize total profit of allocation. In this paper we introduce a new technique to solve assignment problems namely, Divide Row Minima and Subtract Column Minima .For the validity and comparison study we consider an example and solved by using our technique and the existing Hungarian (HA) and matrix ones assignment method(MOA) and compare optimum result shown graphically.
Different situations give rise to the assignment problem, where we must discover an optimal way to assign 'n' objects to 'm' in an bijective function. We have, in this research, propose the possibility of solving exactly the Linear Assignment Problem with a method that would be more efficient than the Hungarian method of exact solution. This method is based on applying a series of pairwise interchanges of assignments to a starting heuristically generated feasible solution, wherein each pairwise interchange is guaranteed to improve the objective function value of the feasible solution.It seems that our algorithm finds the optimal solution which is the same as one found by the Hungarian method, but in much simpler. 7980 M. Khalid et al.
Loading Preview
Sorry, preview is currently unavailable. You can download the paper by clicking the button above.
RELATED TOPICS
- We're Hiring!
- Help Center
- Find new research papers in:
- Health Sciences
- Earth Sciences
- Cognitive Science
- Mathematics
- Computer Science
- Academia ©2024

In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation.
A Comparative Analysis of Assignment Problem
- Conference paper
- First Online: 06 June 2023
- Cite this conference paper

- Shahriar Tanvir Alam ORCID: orcid.org/0000-0002-0567-3381 5 ,
- Eshfar Sagor 5 ,
- Tanjeel Ahmed 5 ,
- Tabassum Haque 5 ,
- Md Shoaib Mahmud 5 ,
- Salman Ibrahim 5 ,
- Ononya Shahjahan 5 &
- Mubtasim Rubaet 5
Part of the book series: EAI/Springer Innovations in Communication and Computing ((EAISICC))
Included in the following conference series:
- International Conference on Big Data Innovation for Sustainable Cognitive Computing
134 Accesses
The aim of a supply chain team is to formulate a network layout that minimizes the total cost. In this research, the lowest production cost of the final product has been determined using a generalized plant location model. Furthermore, it is anticipated that units have been set up appropriately so that one unit of input from a source of supply results in one unit of output. The assignment problem is equivalent to distributing a job to the appropriate machine in order to meet customer demand. This study concentrates on reducing the cost of fulfilling the overall customer demand. Many studies have been conducted, and various algorithms have been proposed to achieve the best possible result. The purpose of this study is to present an appropriate model for exploring the solution to the assignment problem using the “Hungarian Method.” To find a feasible output of the assignment problem, this study conducted a detailed case study. The computational results indicate that the “Hungarian Method” provides an optimum solution for both balanced and unbalanced assignment problems. Moreover, decision-makers can use the study’s findings as a reference to mitigate production costs and adopt any sustainable market policy.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Available as EPUB and PDF
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
- Durable hardcover edition
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Similar content being viewed by others
Optimization model for a production, inventory, distribution and routing problem in small furniture companies.

New Hybrid Algorithm for Supply Chain Optimization
Bi-objective optimization model with economic and environmental consideration for an integrated supply chain with random demand and flexible production rate
Z. Xiang, J. Yang, X. Liang, M.H. Naseem, Application of discrete Grey Wolf Algorithm in balanced transport problem, in 2021 3rd International Academic Exchange Conference on Science and Technology Innovation, IAECST 2021 , (2021), pp. 1312–1318. https://doi.org/10.1109/IAECST54258.2021.9695827
Chapter Google Scholar
C. Woodyard, New York City Is Costliest Place to Park in USA (2018). https://content.usatoday.com/communities/driveon/post/2011/07/new-york-city-costliest-place-to-park-your-car/1#.WWUoFoQrJdg . Accessed 23 Apr 2022
K. McCoy, Drivers spend an average of 17 hours a year searching for parking spots. USA Today (2017). https://www.usatoday.com/story/money/2017/07/12/parking-pain-causes-financial-and-personal-strain/467637001/ . Accessed 23 Apr 2022
W. Ho, P. Ji, A genetic algorithm for the generalised transportation problem. Int. J. Comput. Appl. Technol. 22 (4), 190–197 (2005). https://doi.org/10.1504/IJCAT.2005.006959
Article Google Scholar
Z. Nakat, S. Herrera, Y. Cherkaoui, Cairo Traffic Congestion Study (World Bank, Washington, DC, 2013)
Google Scholar
S. Bussmann, K. Schild, An agent-based approach to the control of flexible production systems, in IEEE International Conference on Emerging Technologies and Factory Automation, ETFA , vol. 2, (2001), pp. 481–488. https://doi.org/10.1109/etfa.2001.997722
S. Emde, M. Gendreau, Scheduling in-house transport vehicles to feed parts to automotive assembly lines. Eur. J. Oper. Res. 260 (1), 255–267 (2017). https://doi.org/10.1016/j.ejor.2016.12.012
Article MathSciNet MATH Google Scholar
S. Chopra, G. Notarstefano, M. Rice, M. Egerstedt, A distributed version of the Hungarian method for multirobot assignment. IEEE Trans. Robot. 33 (4), 932–947 (2017). https://doi.org/10.1109/TRO.2017.2693377
H.A. Hussein, M.A.K. Shiker, Two new effective methods to find the optimal solution for the assignment problems. J. Adv. Res. Dyn. Control Syst. 12 (7), 49–54 (2020). https://doi.org/10.5373/JARDCS/V12I7/20201983
M. Chen, D. Zhu, A workload balanced algorithm for task assignment and path planning of inhomogeneous autonomous underwater vehicle system. IEEE Trans. Cogn. Develop. Syst. 11 (4), 483–493 (2018)
C. Cubukcuoglu, P. Nourian, M.F. Tasgetiren, I.S. Sariyildiz, S. Azadi, Hospital layout design renovation as a quadratic assignment problem with geodesic distances. J. Build. Eng. 44 , 102952 (2021). https://doi.org/10.1016/j.jobe.2021.102952
U. Tosun, A new tool for automated transformation of quadratic assignment problem instances to quadratic unconstrained binary optimisation models. Expert Syst. Appl. 201 , 116953 (2022). https://doi.org/10.1016/j.eswa.2022.116953
S.M. Homayouni, D.B.M.M. Fontes, Production and transport scheduling in flexible job shop manufacturing systems. J. Glob. Optim. 79 (2), 463–502 (2021). https://doi.org/10.1007/s10898-021-00992-6
Article MathSciNet Google Scholar
R. Wang, J. Yan, X. Yang, Neural graph matching network: Learning Lawler’s quadratic assignment problem with extension to hypergraph and multiple-graph matching. IEEE Trans. Pattern Anal. Mach. Intell. 44 (9), 5261–5279 (2022). https://doi.org/10.1109/TPAMI.2021.3078053
T. Dokeroglu, E. Sevinc, A. Cosar, Artificial bee colony optimization for the quadratic assignment problem. Appl. Soft Comput. J. 76 , 595–606 (2019). https://doi.org/10.1016/j.asoc.2019.01.001
X. Xiang, C. Liu, An almost robust optimization model for integrated berth allocation and quay crane assignment problem. Omega (United Kingdom) 104 , 102455 (2021). https://doi.org/10.1016/j.omega.2021.102455
Ö. Karsu, M. Azizoğlu, K. Alanlı, Exact and heuristic solution approaches for the airport gate assignment problem. Omega (United Kingdom) 103 , 102422 (2021). https://doi.org/10.1016/j.omega.2021.102422
A.S. Hameed, M.L. Mutar, H.M.B. Alrikabi, Z.H. Ahmed, A.A. Abdul-Razaq, H.K. Nasser, A hybrid method integrating a discrete differential evolution algorithm with tabu search algorithm for the quadratic assignment problem: A new approach for locating hospital departments. Math. Probl. Eng. 2021 (2021). https://doi.org/10.1155/2021/6653056
S.T. Ngo, J. Jaafar, I.A. Aziz, B.N. Anh, A compromise programming for multi-objective task assignment problem. Computers 10 (2), 1–16 (2021). https://doi.org/10.3390/computers10020015
X. Zheng, D. Zhou, N. Li, T. Wu, Y. Lei, J. Shi, Self-adaptive multi-task differential evolution optimization: With case studies in weapon–target assignment problem. Electronics 10 (23), 2945 (2021). https://doi.org/10.3390/electronics10232945
X. Hu, C. Liang, D. Chang, Y. Zhang, Container storage space assignment problem in two terminals with the consideration of yard sharing. Adv. Eng. Inform. 47 , 101224 (2021). https://doi.org/10.1016/j.aei.2020.101224
Q. Rabbani, A. Khan, A. Quddoos, Modified Hungarian method for unbalanced assignment problem with multiple jobs. Appl. Math. Comput. 361 , 493–498 (2019). https://doi.org/10.1016/j.amc.2019.05.041
A. Kumar, A modified method for solving the unbalanced assignment problems. Appl. Math. Comput. 176 (1), 76–82 (2006). https://doi.org/10.1016/j.amc.2005.09.056
A. Iampang, V. Boonjing, P. Chanvarasuth, A cost and space efficient method for unbalanced assignment problems, in IEEM2010 – IEEE International Conference on Industrial Engineering and Engineering Management , (2010), pp. 985–988. https://doi.org/10.1109/IEEM.2010.5674228
L. Wang, Z. He, C. Liu, Q. Chen, Graph based twin cost matrices for unbalanced assignment problem with improved ant colony algorithm. Results Appl. Math. 12 , 100207 (2021). https://doi.org/10.1016/j.rinam.2021.100207
Download references
Author information
Authors and affiliations.
Military Institute of Science and Technology, Department of Industrial and Production Engineering, Dhaka, Bangladesh
Shahriar Tanvir Alam, Eshfar Sagor, Tanjeel Ahmed, Tabassum Haque, Md Shoaib Mahmud, Salman Ibrahim, Ononya Shahjahan & Mubtasim Rubaet
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Shahriar Tanvir Alam .
Editor information
Editors and affiliations.
Department of Computer Science and Engineering, Sri Eshwar College of Engineering, Coimbatore, Tamil Nadu, India
Anandakumar Haldorai
Department of Computer Science and Engineering, CMR University, Bengaluru, Karnataka, India
Arulmurugan Ramu
Sri Eshwar College of Engineering, Coimbatore, Tamil Nadu, India
Sudha Mohanram
Rights and permissions
Reprints and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper.
Alam, S.T. et al. (2023). A Comparative Analysis of Assignment Problem. In: Haldorai, A., Ramu, A., Mohanram, S. (eds) 5th EAI International Conference on Big Data Innovation for Sustainable Cognitive Computing. BDCC 2022. EAI/Springer Innovations in Communication and Computing. Springer, Cham. https://doi.org/10.1007/978-3-031-28324-6_11
Download citation
DOI : https://doi.org/10.1007/978-3-031-28324-6_11
Published : 06 June 2023
Publisher Name : Springer, Cham
Print ISBN : 978-3-031-28323-9
Online ISBN : 978-3-031-28324-6
eBook Packages : Engineering Engineering (R0)
Share this paper
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research

IMAGES
VIDEO
COMMENTS
The procedure used to solve assignment problems wherein one reduces the original assignment costs to a table of opportunity costs is called _____. stepping-stone method; matrix reduction; MODI method; northwest reduction; simplex reduction; View answer. Correct answer: (B)
This is an unbalanced assignment problem. One way to solve it is to invent a fourth dummy task, perhaps called "sitting still doing nothing", with a cost of 0 for the taxi assigned to it. This reduces the problem to a balanced assignment problem, which can then be solved in the usual way and still give the best solution to the problem.
Step 1: Set up the cost matrix. The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.
The assignment problem is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics. In an assignment problem , we must find a maximum matching that has the minimum weight in a weighted bipartite graph .
In this paper, a new and simple metho d was introduced for solving assignment. problem. This method can b e used for all kinds of assignment problems, whether maximize or minimize ob jective ...
Step VII) we now have exactly one encircled zero in each row and each column of the cost matrix. The assignment schedule corresponding to there zeros is the optimum (maximal) assignment. Note: the above procedure for assignment is Hungarian assignment method Problem 1. Three jobs A B C are to be assigned to three machines x Y Z.
First, we give a detailed review of two algorithms that solve the minimization case of the assignment problem, the Bertsekas auction algorithm and the Goldberg & Kennedy algorithm. It was previously alluded that both algorithms are equivalent. We give a detailed proof that these algorithms are equivalent. Also, we perform experimental results comparing the performance of three algorithms for ...
One of the interesting things about studying optimization is that the techniques show up in a lot of different areas. The "assignment problem" is one that can be solved using simple techniques, at least for small problem sizes, and is easy to see how it could be applied to the real world. Assignment Problem Pretend for a moment that you are writing software for a famous ride sharing ...
5.1 INTRODUCTION. The assignment problem is one of the special type of transportation problem for which more efficient (less-time consuming) solution method has been devised by KUHN (1956) and FLOOD (1956). The justification of the steps leading to the solution is based on theorems proved by Hungarian mathematicians KONEIG (1950) and EGERVARY ...
Definition of Assignment Problem. The statement of the assignment problem is as follows: There are n men and n jobs, with a cost c, for assigning man i to job j. It is required to assign all men to jobs such that one and only one man is assigned to each job and the total cost of the assignments is minimal.
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations. Meaning of Assignment Problem: An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total ...
Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3). Space complexity : O(n^2), where n is the number of workers and jobs.This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional ...
At most one cell can depart an input at a time.! At most one cell can arrive at an output at a time.! Cell arrives at input x and must be routed to output y. x3 x2 x1 y1 y2 y3 inputs outputs 20 Iput-Queued Switching FIFO queueing. Each input x maintains one queue of cells to be routed. Head-of-line blocking (HOL).!
This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver. Example. In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview.
50. The procedure used to solve assignment problems wherein one reduces the original assignment costs to a table of opportunity costs is called _____. A. stepping-stone method B. matrix reduction C. MODI method D. northwest reduction E. simplex reduction 51. The method of finding an initial solution based upon opportunity costs is called
The procedure used to solve assignment problems wherein one reduces the original assignment costs to a table of opportunity costs is called the Hungarian Method. It was developed by the Hungarian mathematician Kőnig D. Jenő. The method aims to reduce the problem to a simpler form in order to find the optimal solution.
Also we compare the optimal solutions among this new method and two existing method .The proposed method isa systematic procedure, easy to apply for solving assignment problem. ... which all elements are one. Thus we solve the problem with the new matrix, by using the new method. ... Method for Solving Assignment Problem Table 2- Eight city TSP ...
The procedure used to solve assignment problems wherein one reduces the original assignment costs to a table of opportunity costs is called _____. a. stepping-stone method b. matrix reduction c. MODI method d. northwest reduction e. simplex reduction correct answer B. The method of finding an initial solution based upon opportunity costs is ...
Hungarian Algorithm Steps. To use the Hungarian Algorithm, we first arrange the activities and people in a matrix with rows being people, columns being activity, and entries being the costs. Once ...
The procedure used to solve assignment problems wherein one reduces the original assignment costs to a table of opportunity costs is called _____. ... The iterative procedure of determining an optimal solution of a minimization transportation problem is known as _____. Unit: 4
The NP hardness proof of the problem is deduced by reduction from the numerical matching with target sum problems. • Two reduction procedures are proposed in order to reduce the size of the problem. • To finalize the assignment procedure, we have used the VNS metaheuristic in order to obtain a good quality complete solution.
Tables 2, 3, 4, and 5 present the steps required to determine the appropriate job assignment to the machine. Step 1 By taking the minimum element and subtracting it from all the other elements in each row, the new table will be: Table 2 represents the matrix after completing the 1st step. Table 1 Initial table of a.