

Using the GCF (Greatest Common Factor) to Solve Problems
In today’s post, we’re going to look at a series of problems that can be solved by using factorization and the GCF (Greatest Common Factor)
First, we’re going to look back at previous blog entries to remind ourselves what the GCF is, and how we calculate the GCF of two numbers:
- Factorization
- Greatest Common Factor
After you’ve refreshed your memory, we’re going to put what we know into practice with an example. After that, we’ll pose two problems for you to solve yourself. Don’t forget to leave us your answer in the comments once you’ve done them!
Example: Solving a problem using the GCF
Rosie and Mark are twins and today is their birthday. Rosie has brought 24 gummy bears to share in class and Mark has brought 18 candy bars. If they want to share their candy with their friends in such a way that all their friends have the same amount of each type of candy and they give out as much candy as possible, how many friends could they give candy to?
The problem requires us to find the maximum quantity of equal groups that we can make with the gummy bears and candy bars, making sure both twins give out the same number of groups. That way, each group will contain the same quantity of gummy bears and candy bars.
To solve this problem, the first thing we have to do is break down both numbers into prime factors.
24 = 2 3 x 3
18 = 2 x 3 2
Now, to calculate the GCF, we need to choose the common factors with the smallest exponent , which in this case will be the 2 and the 3.
Once we’ve chosen our common factors, all we have to do is multiply them by each other. 2 multiplied by 3 equals 6 (2 x 3 = 6).
Therefore, the GCF of 24 and 18 is 6
This means they can make a maximum of 6 groups of each type of candy. 24 gummy bears divided into 6 groups makes 4 gummy bears in each group, and 18 candy bars divided into 6 groups makes 3 candy bars in each group.
So, each one of the 6 friends that are going to get candy from Rosie and Mark are going to get 4 gummy bears and 3 candy bars.
Now you know how it’s done, see if you can solve the following problems without any help!
Problem 1: Practice using the GCF
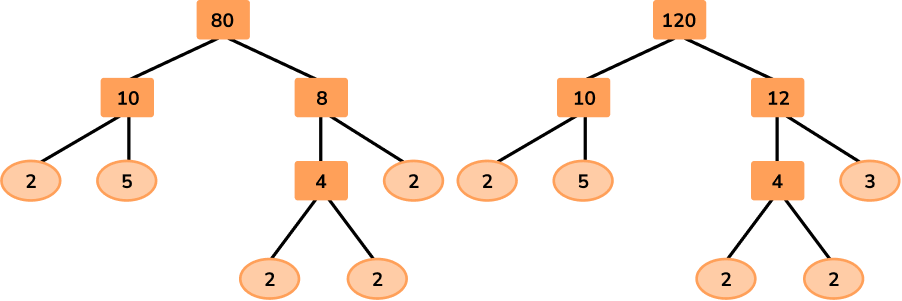
Andy has two ropes. One is 120 feet long, and the other one is 96 feet long. He wants to cut them in such a way that all the pieces are equal, but as long as possible. How many pieces of rope will he get?
Problem 2: Practice using the GCF
A shop buys USB flash drives of different colors wholesale. For Christmas, they made a special order of 84 red flash drives, 196 blue ones, and 252 green ones. To help them store the merchandise neatly, they asked that the flash drives be sent in equal boxes, without mixing any colors, and with each box containing the greatest number of flash drives possible.
If the order is sent in the way the shop requested, how many flash drives will there be in each box, and how many boxes of each color will there be?
I hope these problems have helped you practice and improve your ability to calculate using the GCF!
And don’t forget to leave the solution to each problem in the comments!
If you want to keep practicing, log in to Smartick and try our method for free.
Learn More:
- Greatest Common Factor (GCF): What It Is and How to Calculate It
- Explanation of the Formula to Calculate the Least Common Multiple
- How to Calculate Least Common Multiple
- Solve Fraction Problems with Halves, Thirds and Quarters
- Using Singapore Bars to Help Solve Problems II
- 15 fun minutes a day
- Adapts to your child’s level
- Millions of students since 2009

- Recent Posts
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024
Add a new public comment to the blog: Cancel reply
The comments that you write here are moderated and can be seen by other users. For private inquiries please write to [email protected]
Your personal details will not be shown publicly.
I have read and accepted the Privacy and Cookies Policy
Greatest Common Factor (GCF)
The GCF of two or more non-zero integers, x, and y, is the greatest positive integer m, which divides both x and y. The greatest common factor is commonly known as GCF. Here, greatest can be replaced with highest, and factor can be replaced with divisor. So, the greatest common factor is also known as Highest Common Divisor (HCD), Highest Common Factor (HCF), or Greatest Common Divisor (GCD).
GCF is used almost all the time with fractions, which are used a lot in everyday life. In order to simplify a fraction or a ratio, you can find the GCF of the denominator and numerator and get the required reduced form. Also, if we look around, the arrangement of something into rows and columns, distribution and grouping, all this require the understanding of GCF.
| 1. | |
| 2. | |
| 3. | |
| 4. |
What is Greatest Common Factor (GCF)?
The GCF (Greatest Common Factor) of two or more numbers is the greatest number among all the common factors of the given numbers. The GCF of two natural numbers x and y is the largest possible number that divides both x and y without leaving any remainder . To calculate GCF, there are three common ways- division, multiplication , and prime factorization.
Example: Let us find the greatest common factor of 18 and 27.
First, we list the factors of 18 and 27 and then we find out the common factors.
Factors of 18 : 1, 2, 3, 6, 9, 18
Factors of 27 : 1, 3, 9, 27
The common factors of 18 and 27 are 1, 3, and 9. Among these numbers, 9 is the greatest (largest) number. Thus, the GCF of 18 and 27 is 9. This is written as: GCF(18, 27) = 9.
A factor of a number is its divisor as well. Hence the greatest common factor is also called the Greatest Common Divisor (or) GCD . In the above example, the greatest common divisor (GCD) of 18 and 27 is 9 which can be written as:
GCD (18, 27) = 9.
How to Find GCF?
Following are the three methods for finding the greatest common factor of two numbers:
- Listing out common factors
- Prime factorization
- Division method
GCF by Listing Factors
In this method, factors of both the numbers can be listed, then it becomes easy to check for the common factors. By marking the common factors, we can choose the greatest one amongst all of them. Let's look at the example given below:
Example: What is the GCF of 30 and 42?
- Step 1 - List out the factors of each number.
- Step 2 - Mark all the common factors.
- Step 3 - 6 is the common factor and the greatest one.
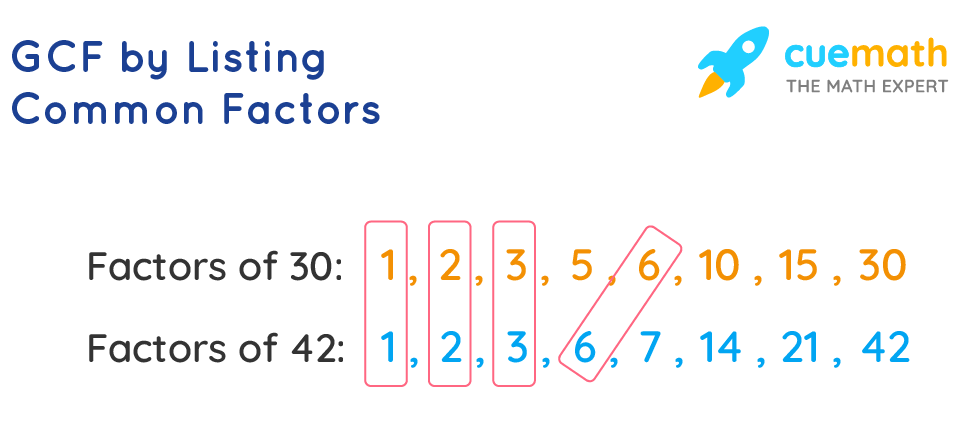
Therefore, GCF of 30 and 42 = 6. This method can be used for finding GCF of three or more numbers as well.
Finding the greatest common factor by listing factors may be difficult if the numbers are bigger. In such cases, we use the prime factorization and division methods for finding GCF.
GCF by Prime Factorization
Prime factorization is a way of expressing a number as a product of its prime factors, starting from the smallest prime factor of that number. Let's look at the example given below:
Example: What is the GCF of 60 and 90?
- Step 1 - Represent the numbers in the prime factored form.
- Step 2 - GCF is the product of the factors that are common to each of the given numbers.

Thus, GCF (60,90) = 2 1 × 3 1 × 5 1 = 30. Therefore, GCF of 60 and 90 = 30. We can also find the greatest common factor of three numbers or more by this method.
Finding GCF by Division Method
The division is a method of grouping objects in equal groups, whereas for large numbers we follow long division , which breaks down a division problem into a series of easier steps. The greatest common factor (GCF) of a set of whole numbers is the largest positive integer that divides all the given numbers, without leaving any remainder. Let's look at the example given below:
Example: Find the GCF of 198 and 360 using the division method.
Among the given two numbers, 360 is the larger number and 198 is the smaller number.
- Step 1 - Divide the larger number by the smaller number using long division.
- Step 2 - If the remainder is 0, then the divisor is the GCF. If the remainder is not 0, then make the remainder of the above step as the divisor and the divisor of the above step as the dividend and perform long division again.
- Step 3 - If the remainder is 0, then the divisor of the last division is the GCF. If the remainder is not 0, then we have to repeat step 2 until we get the remainder 0.

Therefore, the GCF of the given two numbers is the divisor of the last division. In this case, the divisor of the last division is 18. Therefore, the GCF of 198 and 360 is 18. This method is the most appropriate method for finding GCF of large numbers. Let us see how to use the division method to find the greatest common factor of three numbers. In order to find the GCF of three numbers by long division, the following steps are to be followed:
- First, we will find the GCF of two of the numbers.
- Next, we will find the GCF of the third number and the GCF of the first two numbers.
Example: Find the GCF of 126, 162, and 180.
First, we will find the GCF of the two numbers 126 and 162. [You can choose any two numbers out of the given three numbers]

Thus, GCF of 126 and 162 = 18 ........(1).
Next, we will find the GCF of the third number, which is 180, and the above GCF 18 by using the same method.

Thus, GCF of 180 and 18 = 18 ......(2).
From (1) and (2), GCF(126, 162, 180) = 18. Therefore, GCF of 126, 162, and 180 = 18.
GCF and LCM
The greatest common factor is the largest number that divides the given numbers without leaving any remainder. On the other hand, the LCM (least common multiple) Is the smallest common multiple of the given numbers that can be divided by the given numbers exactly, without leaving a remainder. For example, let us find the GCF and LCM of numbers 6 and 8.
The factors of 6 are 1, 2, 3, 6, and the factors of 8 are 1, 2, 4, 8. So, the common factors of 6 and 8 are 1 and 2, out of which 2 is the highest common factor. Thus, GCF (6, 8) = 2. Now, the first few multiples of 6 are 6, 12, 18, 24, 30, ..., and the first few multiples of 8 are 8, 16, 24, 32, ... Out of these, the least common multiple of 6 and 8 is 24. Thus, LCM (6, 8) = 24.
One very interesting relation between GCF and LCM of two numbers is that the product of GCF and LCM of two numbers is equal to the product of the numbers. For any two numbers a and b, we have, LCM (a, b) × GCF (a, b) = a × b. Let us verify it using the above example of 6 and 8. Let a = 6 and b = 8.
LCM (6, 8) × GCF (6, 8) = 6 × 8
24 × 2 = 6 × 8
Hence verified.
Now, let us learn the difference between GCF and LCM in the section below.
Difference between GCF and LCM
The GCF or the greatest common factor of two or more numbers is the greatest factor among all the common factors of the given numbers, whereas the LCM or the least common multiple of two or more numbers is the smallest number among all common multiples of the given numbers. The following table shows the difference between GCF and LCM:
| Greatest Common Factor(GCF) | Least Common Multiple(LCM) |
|---|---|
| The GCF of two natural numbers a and b is the greatest natural number x, which is a factor of both a and b. | The LCM of two natural numbers a and b is the smallest number y, which is a multiple of both a and b. |
| In the intersection of the sets of common factors, it is the greatest value. | In the intersection of the sets of common multiples, it is the minimum value. |
| Represented as, GCF(a, b) = x | Represented as, LCM(a, b) = y |
► Related Topics
Check these articles related to the concept of the greatest common factor (GCF) in math.
- Factoring Methods
- GCF Calculator
- GCF Formula
Greatest Common Factor Examples
Example 1: Find the GCF of 6, 12, and 36 by using the listing factors method.
The given numbers are 6, 12, and 36. We will find the factors of each of these numbers. Then, circle the common factors.

In this example, 1, 2, 3, and 6 are all common factors of 6, 12, and 36. Out of all these common factors, 6 is the greatest, and hence, GCF(6,12,36) = 6.
Example 2: Find the GCF of 168, 252, and 288 by the prime factorization method.
The given numbers are 168, 252, and 288. We will find the prime factorization of each of these numbers.

Thus, GCF (168,252,288) = 2 × 2 × 3 = 2 2 × 3 1 . The GCF of these three numbers will be the product of the common prime factors of all three numbers. Thus, GCF of 168, 252 and 288 = 2 2 × 3 1 = 12.
Example 3: Find the GCF of 9000 and 980 using the division method.
Among the given numbers, 9000 is the largest, and 980 is the smallest. We will divide the larger number by the smaller number. Next, we will make the remainder as the divisor and the last divisor as the dividend and divide again. We will repeat this process until the remainder is 0.

Therefore, the GCF of 9000 and 980 is 20.
go to slide go to slide go to slide

Book a Free Trial Class
Practice Questions on GCF
go to slide go to slide
FAQs on GCF
What is meant by greatest common factor (gcf).
The greatest number among all the common factors of two or more numbers is called the greatest common factor or GCF. For any two numbers , the GCF is the largest number that divides the two given numbers. GCF can be calculated by using the basic arithmetic operations in mathematics i.e. division, multiplication, and prime factorization.
How to Find the Greatest Common Factor (GCF)?
To find the greatest common factor of two or more natural numbers , there are 3 methods that can be used - listing out of the common factors, prime factorization, and division method. Each method requires division and multiplication to obtain the GCF. For example, the GCF of 14 and 35 is 7. By using the listing common factors method, the factors of 14 are 1, 2, 7, 14 and the factors of 35 are 1, 5, 7, 35. The two common factors are 1 and 7 out of which 7 is the largest. Therefore, 7 is the GCF of 14 and 35.
What is the Greatest Common Factor of Two Prime Numbers?
A prime number has only two factors (1 and itself). Hence, two prime numbers cannot have any common factor other than 1. Therefore, the greatest common factor of two prime numbers is always 1. For example, the greatest common factor of 5 and 7 is 1.
What is the Greatest Common Factor of 24 and 54?
The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24. The factors of 54 are 1, 2, 3, 6, 9, 18, 27, and 54. The common factors of 24 and 54 are 1, 2, 3, and 6. Hence, the GCF of 24 and 54 is 6.
What is the GCF of 15 and 20?
The factors of 15 are 1, 3, 5, and 15. The factors of 20 are 1, 2, 4, 5, 10, and 20. The common factors of 15 and 20 are 1 and 5. Thus, the GCF of 15 and 20 is 5.
How to Find GCF and LCM?
GCF (greatest common factor) and LCM (least common multiple) can be found by any of the methods written below:
- Listing method
- Prime factorization method
All the methods are used differently for GCF ad LCM.
Are GCF and HCF the Same?
The greatest common factor is abbreviated as GCF and is also known as the Highest Common Factor (HCF). So, yes, GCF and HCF are the same.
Is GCF Greater Than LCM?
The LCM is the least common multiple of the given numbers that can be divided by both the numbers, while the GCF is the greatest common factor of the given numbers that divide both the numbers. Thus, for any two numbers, the LCM of the numbers is greater than the GCF of the numbers.
How to Find the Greatest Common Factor of a Polynomial?
The greatest common factor of a polynomial can be found by following the steps listed below:
- Step 1: Observe all the terms of the given polynomial carefully.
- Step 2: Find the numbers or variables that are common in all the terms.
That will be the required GCF of polynomial.
How do you Factor Out the GCF?
GCF of two or more numbers can be obtained by using the prime factorization method that is done only in a few steps. They are:
- List out the prime factors of all the numbers.
- Circle the common prime factors among all the numbers.
- Multiply all the circled numbers to find the GCF.
Use List Method to Find GCF
Finding the greatest common factor using the list method.
The greatest common factor , also known as GCF , of two numbers is the largest number that can evenly divide the given two numbers.
Another way to define GCF: The greatest common factor of two numbers is the largest factor that is common to both numbers.
The two definitions above mean the same thing.
Don’t be confused if you encounter other names of the greatest common factor. They all have the same meaning. The alternate names of GCF are:
- Greatest Common Divisor which is abbreviated as GCD
- Highest Common Factor which is abbreviated as HCF

Before you continue, make sure that you know how to find all the factors of a number. Otherwise, please review my short lesson on how to find all factors of a number using the rainbow method .
Steps on How to Find the Greatest Common Factor
Step 1: List or write ALL the factors of each number.
Step 2: Identify the common factors. You can do that by encircling each common factor or drawing a line segment between them. It’s really up to you how you want to mark the common factors so they stand out.
Step 3: After identifying the common factors, select or choose the number which has the largest value. This number will essentially be the Greatest Common Factor (GCF).
Examples of How to Find the Greatest Common Factors
NOTE: I decided to focus on finding the GCF of two numbers because they are the most common problems that you will encounter when studying GCF.
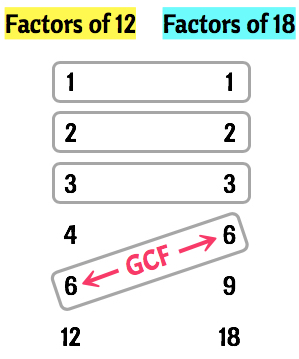
Example 1 : Find the Greatest Common Factor of [latex]12[/latex] and [latex]18[/latex].
This problem is easy because the numbers involved are relatively simple. You should be able to find all the factors of 12 and 18 using the rainbow method . As an alternative, I have listed all the factors of numbers from 1 to 100 for you to use at your own convenience.
So here are all the factors of both [latex]12[/latex] and [latex]18[/latex].
Factors of 12 : 1, 2, 3, 4, 6, 12
Factors of 18 : 1, 2, 3, 6, 9, 18

After listing all the factors of each number, we now identify the common factors. As you can see below, the common factors of [latex]12[/latex] and [latex]18[/latex] are [latex]1[/latex], [latex]2[/latex], [latex]3[/latex], and [latex]6[/latex]. Notice that I identified the common factors by enclosing them in a “rectangle”.

So what is the GCF then? Obviously, the GCF is one of the common factors. The common factor which has the largest value is actually the Greatest Common Factor. Therefore the GCF of [latex]12[/latex] and [latex]18[/latex] is [latex]6[/latex]. That’s it!
Example 2 : Find the Greatest Common Factor of [latex]64[/latex] and [latex]96[/latex].
In many instances in math, as the number becomes larger, the level of difficulty of the problem also increases. Yes, this is true as well when finding the GCF of two large numbers. However, the concept or procedure never changes.
So here we go. Let’s find the complete factors of [latex]64[/latex] and [latex]96[/latex].
◉ The complete factors of [latex]64[/latex] are 1, 2, 4, 8, 16, 32, and 64.
◉ While the complete factors of [latex]96[/latex] are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96.
Below are the lists of factors in a vertical format.
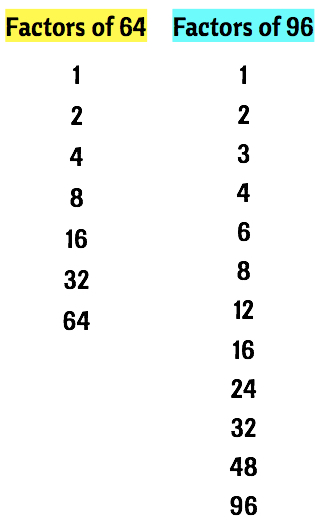
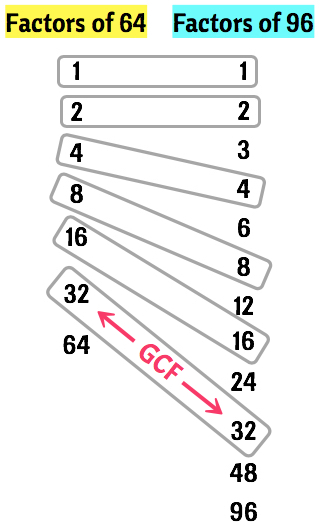
The next step is to compare the lists of factors. Then draw a shape so that the common factor is inside each shape. You can be creative here! Notice that on the illustration below, we have six (6) common factors which are [latex]1[/latex], [latex]2[/latex], [latex]4[/latex], [latex]8[/latex], [latex]16[/latex], and [latex]32[/latex].
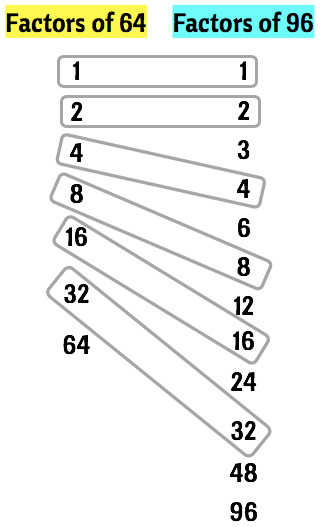
By looking at the common factors, the one which has the biggest value is [latex]32[/latex]. Therefore, the greatest common factor of [latex]64[/latex] and [latex]96[/latex] is simply [latex]32[/latex].
Example 3 : Determine the Greatest Common Factor of [latex]42[/latex] and [latex]126[/latex].
It is easy to rush into solving a math problem because you are already familiar with the steps on how to work it out. However, it is a good practice to pause or step back and look at the problem from a broader perspective before delving into the process of solving the problem itself.
The reason is, that the procedure that you already know may not be the most time-efficient because there might be a better way, that is, a shorter solution.
Let’s approach it this way. If [latex]42[/latex] can divide [latex]126[/latex] without a remainder, then it implies that [latex]42[/latex] is a factor of [latex]126[/latex]. Not only that [latex]42[/latex] is a common factor of [latex]42[/latex] and [latex]126[/latex], but it is also the common factor that has the highest value.
If you think about it, it is not possible to have a common factor greater than [latex]42[/latex] because it cannot be more than the smaller number of the given two numbers.
So, does [latex]42[/latex] divide [latex]126[/latex] evenly? The answer is yes! Therefore, the greatest common divisor (GCD) of [latex]42[/latex] and [latex]126[/latex] is simply [latex]42[/latex]. Done!
Example 4 : What is the GCF of [latex]71[/latex] and [latex]223[/latex] ?
Just like with example #3 , don’t jump into the motion of applying the steps that you already know. I can’t overemphasize the importance of practicing restraint when solving math problems in general. Stepping back to see the big picture is extremely important because this will allow you to strategize and therefore be able to devise a viable approach to the problem.
So now, if you closely examine the two numbers which are [latex]71[/latex] and [latex]223[/latex], you should easily recognize that both of them are prime numbers. Remember that a prime number has exactly two factors which are [latex]1[/latex] and itself. In other words, we can say that a prime number is only divisible by [latex]1[/latex] and itself.
Listing the factors of [latex]71[/latex] and [latex]223[/latex]:
Factors of 71 : 1, 71
Factors of 223 : 1, 223
We should be able to conclude that since [latex]1[/latex] is the ONLY common factor, it implies that [latex]1[/latex] must also be the greatest common factor by default. Thus, [latex]{\rm{gcf}}\left( {71,223} \right) = 1[/latex].
Example 5 : What is the GCF of [latex]72[/latex] and [latex]84[/latex] ?
First, we know that both numbers are not prime, in fact, both are even numbers. It means they have common factors other than [latex]1[/latex]. Secondly, it is obvious too that the smaller number [latex]72[/latex] cannot evenly divide the larger number [latex]84[/latex]. This leaves us to conclude that the smaller of the two numbers, [latex]72[/latex], is NOT the greatest common factor either.
Well, the only option left is to proceed with the step-by-step procedure of finding the GCF of two numbers as discussed in the first part of this lesson.
Listing all the factors of each number, we have:
Factors of 72 : 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Factors of 84 : 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84

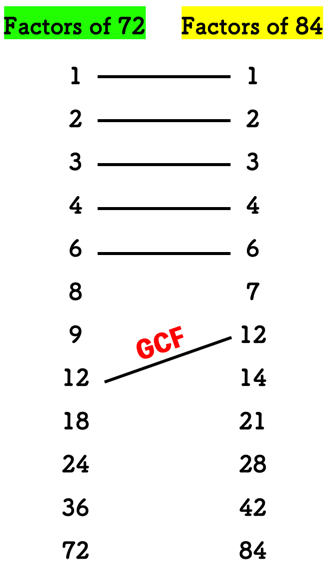
Comparing the lists of factors, the common factors of 72 and 84 are 1, 2, 3, 4, 6, and 12.
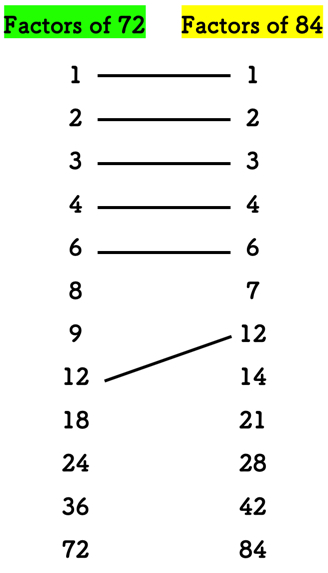
Taking it from the diagram, [latex]12[/latex] is the greatest common factor of [latex]72[/latex] and [latex]84[/latex]. Done!
You might also like these tutorials:
- Use Prime Factorization to Find GCF
- Finding LCM using the List Method
- Use Prime Factorization to Find LCM
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Understanding multiplication
Add and subtract within 100
GCF and LCM
Here you will learn about GCF and LCM (greatest common factor and least common multiple), including how to find the GCF and LCM of two or more numbers using the prime factorization method and recognize when to find the GCF or the LCM in word problems.
Students will first learn about GCF and LCM as part of the number system in 6th grade.
What is GCF and LCM?
GCF and LCM are two abbreviations for the greatest common factor (GCF) and the least common multiple (LCM).
The greatest common factor (GCF) is the largest whole number that two or more numbers can be divided by. The lowest common multiple (LCM) is the smallest whole number which is a multiple of two or more whole numbers.
Let’s take a look at some examples below:
- Example of GCF , also known as the greatest common divisor (GCD) and the highest common factor (HCF). Find the GCF of 8 and 12. Let’s start by writing the factors of 8 and 12. Factors of {\bf{8}} {\textbf{: }} 1, 2, 4, 8 Factors of {\bf{12}} {\textbf{: }} 1, 2, 3, 4, 6, 12 There are several numbers that occur in both lists ( 1, 2, and 4 ). The largest factor that occurs in each list is 4, and so the greatest common factor of 8 and 12 is \bf{4}.
- Example of LCM Find the LCM of 8 and 12. Let’s start by writing the first 12 multiples of 8 and 12. Multiples of {\bf{8}} {\textbf{: }} 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96 Multiples of {\bf{12}} {\textbf{: }} 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144 There are several values that occur in both lists ( 24, 48, 72, and 96 ). The lowest of these is 24, hence the least common multiple of 8 and 12 is \bf{24}.
Prime factor decomposition
To calculate the GCF or LCM of two or more numbers, you can write out a list of factors or multiples as we have above, however, this approach can be very time consuming and can be complicated when dealing with factors and multiples of large numbers ( 3 digit numbers in particular).
You can therefore use prime factorization to find these values.
The fundamental theorem of arithmetic states that every positive whole number greater than one is either a prime number, or can be written as a product of its prime factors. Every number has a unique set of numbers called prime factors.
By presenting prime factors within a Venn diagram , you can quickly determine both the GCF and LCM of the two or more numbers in the question.
For example,
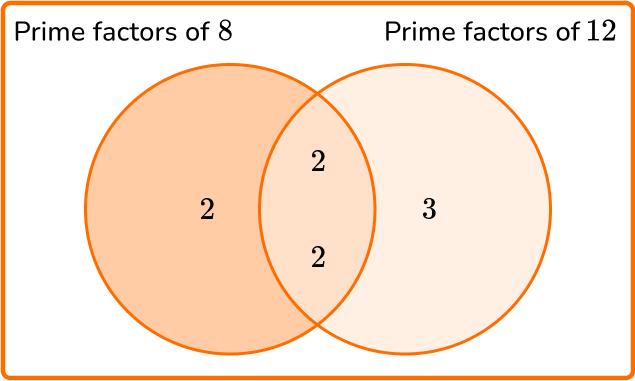
8=2\times{2}\times{2}
12=2\times{2}\times{3}
The intersection of the two circles contains the greatest common factor , where you multiply the values within the intersection together .
Here, the GCF of 8 and 12 is equal to 2\times{2}=4.
The union of the two circles contains the least common multiple where you multiply the values within both circles together .
Here, the LCM of 8 and 12 is equal to 2\times(2\times{2})\times{3}=24.
As the least common multiple is found by multiplying all of the factors together within the Venn diagram, the least common multiple can be found by multiplying the greatest common factor by the remaining prime factors.
This allows you to solve problems where you are given the GCF and LCM of two numbers and you need to determine the original two numbers.
Common Core State Standards
How does this relate to 6th grade math?
- Grade 6 – The Number System (6.NS.4) Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers (1–100) with a common factor as a multiple of a sum of two whole numbers with no common factor. For example, express 36 + 8 \, as \, 4 (9 + 2).
![example of problem solving in gcf [FREE] GCF and LCM Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/01/GCF-and-LCM-Worksheet-listing-image.png)
[FREE] GCF and LCM Worksheet (Grade 6 to 8)
Use this worksheet to check your grade 6 to 8 students’ understanding of the greatest common factors and lowest common multiples of numbers. 15 questions with answers to identify areas of strength and support!
How to find the greatest common factor
In order to find the greatest common factor of two or more numbers:
State the product of prime factors for each number.
Write all the prime factors for each number into a Venn diagram.
Multiply the prime factors in the intersection to find the GCF.
How to find the least common multiple
In order to find the least common multiple of two or more numbers:
Multiply each prime factor in the Venn diagram to find the LCM.
GCF and LCM examples
Example 1: gcf of two simple composite numbers.
Find the greatest common factor of 30 and 42.
2 Write all the prime factors for each number into a Venn diagram.
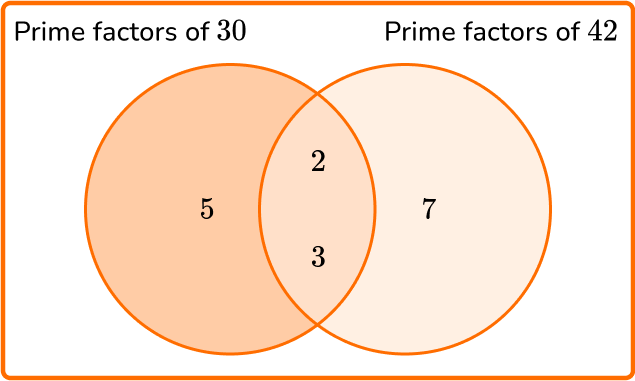
3 Multiply the prime factors in the intersection to find the GCF.
GCF =2\times{3}=6.
Example 2: LCM of two simple composite numbers
Calculate the least common multiple of 16 and 18.
16=2\times{2}\times{2}\times{2}
18=2\times{3}\times{3}
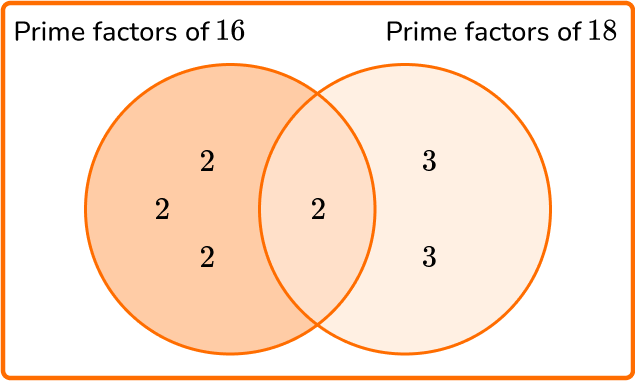
LCM =(2\times{2}\times{2})\times{2}\times(3\times{3})=8\times{2}\times{9}=144.
Example 3: GCF word problem
120 \ ml of red paint and 156 \ ml of blue paint are mixed together to create a tin of purple paint. The paint is then distributed equally into sample tubes. Each tube must contain the same amount of paint that must be over 20 \ ml.
What is the maximum number of tubes that can be filled with the minimum amount of paint?
120=2\times{2}\times{2}\times{3}\times{5}
156=2\times{2}\times{3}\times{13}
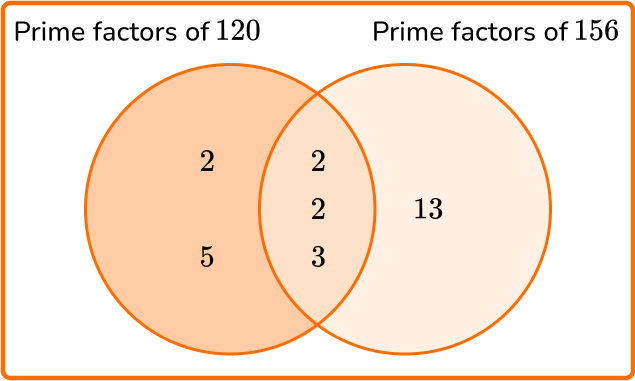
GCF =2\times{2}\times{3}=12.
The total amount of paint is 120 + 156 = 276 \ ml.
Dividing 276 \ ml into 12 equal shares (the GCF), we have
276\div{12}=23.
As each tube must contain over 20 \ ml of paint, we must have 12 tubes, each containing 23 \ ml of paint.
Example 4: LCM word problem
A plumber is fixing multiple leaking pipes. Pipe A drips water every 12 seconds. Pipe B drips water every 22 seconds. Both pipes drip at the same time. How much time passes before they next drip at the same time? Write your answer using minutes and seconds.
22=2\times{11}
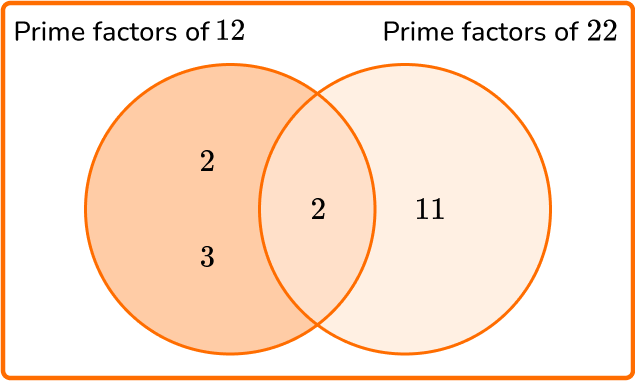
LCM =(2\times{3})\times{2}\times{11}=6\times{2}\times{11}=132
132 seconds pass. Converting this to minutes and seconds is 2 minutes and 12 seconds ( 60 + 60 + 12 = 132 , with 60 seconds = 1 minute).
How to find the original values given the GCF and the LCM
In order to find the original values given the GCF and the LCM:
- Divide the LCM by the GCF.
Calculate the product of primes of the remainder.
Determine which prime factors match each original number.
Example 5: find the numbers, given the GCF
The greatest common factor of 3 numbers is 7. The product of their remaining prime factors is 30 and each number is greater than 10. Determine the value of the three numbers.
Divide the LCM by the GCF to determine the remainder.
As we already know the remainder ( 30 ), we can move on to step 2.
Using a prime factor tree, the product of primes for 30 is:
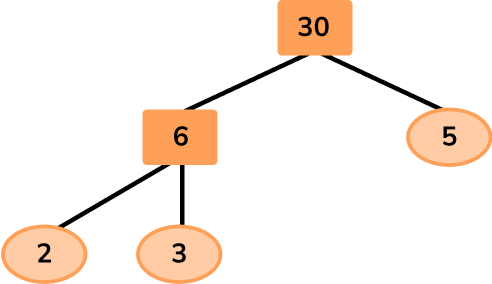
30=2\times{3}\times{5}
As each value is greater than 10, the GCF 7 must be a factor of all 3 numbers and it must be multiplied by another factor. 30 has 3 prime factors, 2, 3, and 5 and so the original three numbers are:
A=7\times{2}=14
B=7\times{3}=21
C=7\times{5}=35
Example 6: find the original numbers given the GCF and LCM
Two numbers, A and B, have the following number properties:
- GCF (A,B) = 7
- LCM (A,B) = 2,310
- A is divisible by 3
- B is an even number
- 100<A<B
Determine the values of A and B.
2310\div{7}=330
Using a prime factor tree, the product of primes for 330 is:
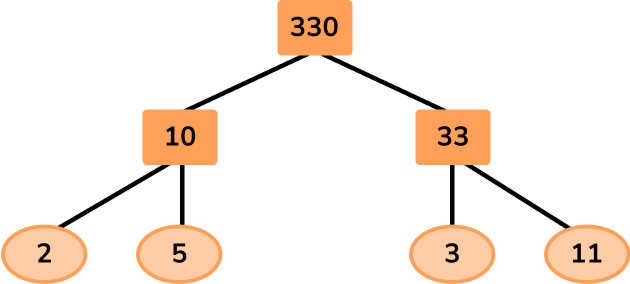
330=2\times{3}\times{5}\times{11}
As A is divisible by 3, two factors of A must be 3 and 7 (the GCF).
As B is even, two factors of B must be 2 and 7 (the GCF).
Writing this up so far, we have
A=3\times{7}\times{x}
B=2\times{7}\times{y}
As 330=2\times{3}\times{5}\times{11}, we have the remaining factors of 5 and 11 to place.
As 100<A<B, both A and B are greater than 100 with A being smaller than B. The only way this is possible is by making x=5 and y=11.
This means that,
A=3\times{7}\times{5}=105
B=2\times{7}\times{11}=154
The solution is A = 105 and B = 154.
Tips for teaching GCF and LCM
- Before introducing GCF and LCM, students should have a strong understanding of factors and multiples, which they would have first learned in 4th grade. Review these terms and practice listing factors and multiples if needed.
Easy mistakes to make
- Finding the GCF instead of the LCM (and vice versa) A very common misconception is mixing up the greatest common factor with the least common multiple. Factors are composite numbers that are split into smaller factors. Multiples are composite numbers that are multiplied to make larger numbers.
- Incorrect evaluation of powers It is possible to write prime factors into a Venn diagram with their associated exponent or power. This only becomes an issue when the powers are not correctly interpreted. We suggest having students write the prime factors without the use of exponents. Take, for example, the numbers 12 and 18. 12=2^{2}\times{3} 18=2\times{3}^{2} Here, 2^{2}=2\times{2}=4 which is correct, however, the same misconception could then be continued to 3^{2}=3\times{2}=6, which is incorrect. Instead, 3^{2}=3\times{3}=9. This will have an impact on the value of the GCF and the LCM.
Related lessons on factors and multiples
- Factors and multiples
- Factor tree
- Least common multiple
- Greatest common factor
- Prime factors
- Factor pairs
Practice GCF and LCM questions
1. Find the GCF of 54 and 60.

GCF (54,60) = 2\times{3}=6
2. Find the LCM of 24 and 32.

LCM (24,32) = 3\times(2\times{2}\times{2})\times(2\times{2})=3\times{8}\times{4}=96
3. Two lengths of ribbon measure 1.2 \ m and 80 \ cm. Each piece of ribbon needs to be cut into the fewest number of pieces of the same length. What is the length of each piece?
GCF (80,120) = 2\times{2}\times{2}\times{5}=40
4. Two runners leave the start line of a 200 \ m track on the whistle. It takes runner A \ 1 minute to run 1 lap of the track and runner B \ 1 minute and 12 seconds. What distance will runner B have traveled when they next cross the start line at the same time?
Converting both lap times to seconds, runner A takes 60 seconds, and runner B takes 72 seconds.
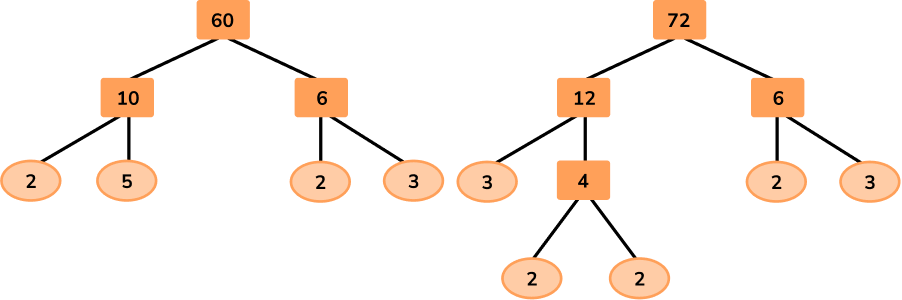
GCF (60,72)=2\times{2}\times{3}=12
LCM (60,72) = 5 \times 12 \times (2 \times 3)=5 \times 12 \times 6=360
360 seconds = 6 minutes
6\div{1.2}=5 laps
5. The greatest common factor of two numbers is 35. The product of the remaining factors is 33. Both original numbers contain three digits. What is the difference between the two original numbers?
Smaller number: 35\times{3}=105
Larger number: 35\times{11}=385
6. Two numbers x and y have the following number properties:
- \text{LCM }(x,y)=96
- \text{GCF }(x,y)=8
- 2<x<y<40
What is the value of x+y?
GCF and LCM questions
1. A farm needs to divide their two fields into equal-sized enclosures for some horses. Field 1 is 240 \ m^2. Field 2 is 160 \ m^2. Each horse must have at least 42 \ m^2.
(a) What is the minimum possible area for each enclosure?
(b) What is the maximum number of horses that can use these two fields?
240=2^4 \times 3 \times 5 \, or \, 240=2 \times 2 \times 2 \times 2 \times 3 \times 5
160=2^5 \times 5 \, or \, 160=2 \times 2 \times 2 \times 2 \times 2 \times 5
GCF (240,160)=80 \ m^2
2+3=5 \, or \, (240+160) \div 80=5
2. Given that 6480=2^4 \times 3^4 \times 5, simplify the ratio 10800:6480.
GCF (10800,6480)=2^4 \times 3^3 \times 5
Remaining factors are 5 (for 10800 ) and 3 (for 6480 ).
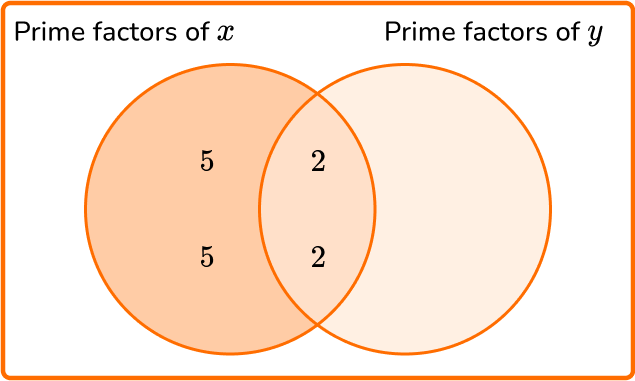
3. The least common multiple of x and y is 2^3 \times 3^2 \times 5^2 where x is a square number such that 36<x<225.
(a) Find the exact value of x.
(b) The greatest common factor of x and y is 4. Determine the value of y. Use the Venn diagram below to help you.
x=2^2 \times 5^2 or
GCF and LCM FAQs
Step 1: State the product of prime factors for each number. Step 2: Write all the prime factors for each number into a Venn diagram. Step 3: Multiply the prime factors in the intersection to find the GCF.
Step 1: State the product of prime factors for each number. Step 2: Write all the prime factors for each number into a Venn diagram. Step 3: Multiply each prime factor in the Venn diagram to find the LCM.
To find the GCF, list all prime factors that are common between the two numbers and multiply them together. To find the LCM, multiply the GCF by all the prime factors of both numbers that have not yet been used.
The least common denominator (LCD) is the least common multiple (LCM) of the denominators of two or more fractions.
The next lessons are
- Converting fractions, decimals, and percentages
- Fractions operations
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!
Privacy Overview
Greatest Common Factor
What is greatest common factor, how we can find the gcf of two numbers.
- LCM Versus GCF
Real-life Applications of Greatest Common Factor
Solved examples.
- Practice problems
Frequently Asked Questions
The Greatest Common Factor (GCF), also known as the Greatest Common Divisor/Greatest Common Denominator (GCD) or Highest Common Factor (HCF) of two or more integers is the largest positive integer that divides each of the numbers without leaving a remainder. In other words, it is the greatest number that is a common factor of the given numbers.
For example, consider the numbers `12` and `18`. The factors of `12` are `1`, `2`, `3`, `4`, `6`, and `12`. The factors of `18` are `1`, `2`, `3`, `6`, `9`, and `18`. The common factors are `1`, `2`, `3`, and `6`. Among these, the greatest common factor is `6`. Therefore, GCF`(12, 18) = 6`.
The GCF is often denoted as GCF`(a, b)`, where "`a`" and "`b`" are the numbers for which we want to find the greatest common factor.
The GCF is a fundamental concept in number theory and has various applications in mathematics, including simplifying fractions , factoring polynomials, and solving equations. It helps identify the largest factor that two or more numbers share, making it a useful tool in many mathematical problems.
Finding the Greatest Common Factor (GCF) involves identifying the largest positive integer that divides two or more numbers without leaving a remainder. Here's a step-by-step guide on how to find the GCF:
Method `1`: Listing Factors
Step `1`. List the factors of each number.
- Identify all the positive integers that evenly divide each of the given numbers.
Step `2`. Find the common factors.
- Determine the common factors that both numbers share.
Step `3`. Identify the greatest common factor.
- The GCF is the largest among the common factors.
Example: Find the GCF of `24` and `36`.
Factors of `24`: `1, 2, 3, 4, 6, 8, 12, 24`
Factors of `36`: `1, 2, 3, 4, 6, 9, 12, 18, 36`
Common factors: `1, 2, 3, 4, 6, 12`
GCF`(24, 36) = 12`
Method `2`: Prime Factorization
Step `1`. Find the prime factorization of each number.
- Express each number as a product of prime numbers .
Step `2`. Identify common prime factors.
- Determine the prime factors that both numbers share.
Step `3`. Multiply the common prime factors.
- Multiply the common prime factors to find the GCF.
Example: Find the GCF of `48` and `60`.
- Prime factorization of `48`: \(2^4 \times 3^1\)
- Prime factorization of `60`: \(2^2 \times 3^1 \times 5^1\)
Common prime factors: \(2^2 \times 3^1\)
GCF`(48, 60) =` \(2^2 \times 3^1 = 12\)
Both methods will give you the same result. Choose the method that you find most comfortable or efficient for a particular set of numbers.
Method `3`: Division Method
Finding the Greatest Common Factor (GCF) using the division method involves repeated division until the remainder is zero. Here's a step-by-step guide on how to find the GCF using this method:
Step `1`: Choose two numbers.
- Select the two numbers for which you want to find the GCF.
Step `2`: Divide the larger number by the smaller number.
- Divide the larger number by the smaller number. Record the quotient and remainder.
Step `3`: Replace the larger number.
- Replace the larger number with the smaller number, and the smaller number with the remainder obtained in the previous step.
Step `4`: Repeat steps `2` and `3`.
- Continue the process of dividing the new larger number by the new smaller number until the remainder is zero. The last non-zero remainder is the GCF.
Example: Find the GCF of `48` and `60`.
`1`. \(60 \div 48 = 1\) with a remainder of `12`. Replace `60` with `48` and `48` with `12`.
`2`. \(48 \div 12 = 4\) with no remainder. The GCF is the last non-zero remainder, which is `12`.
Therefore, GCF`(48, 60) = 12`.
This method is also known as the Euclidean Algorithm and is a systematic way to find the GCF of two numbers. It is efficient and commonly used in practice.
Important Note: The GCF of a set of prime numbers will always be `1` because two or more prime numbers have no common factor other than `1`.
LCM Versus GCF
The Greatest Common Factor (GCF) and the Least Common Multiple (LCM) are two different concepts in number theory, and they serve different purposes in mathematics. As GCF and LCM are often confused lets look at them individually.
`1`. Greatest Common Factor (GCF):
The GCF of two or more numbers is the largest positive integer that divides each of the numbers without leaving a remainder.
For example, the GCF of `12` and `18` is `6` because `6` is the largest number that divides both `12` and `18` without a remainder `(12 ÷ 6 = 2, 18 ÷ 6 = 3)`.
The GCF is useful for simplifying fractions, factoring polynomials, and solving equations.
`2`. Least Common Multiple (LCM):
The LCM of two or more numbers is the smallest positive integer that is a multiple of each of the numbers.
For example, the LCM of `4` and `6` is `12` because `12` is the smallest number that is divisible by both `4` and `6 (4 × 3 = 12, 6 × 2 = 12)`.
The LCM is used in problems involving multiple cycles or periods, such as finding a common denominator for fractions.
Key Differences:
- The GCF is concerned with finding the largest common factor of numbers, while the LCM is concerned with finding the smallest common multiple.
- The GCF is a divisor of the given numbers, while the LCM is a multiple of the given numbers.
- The GCF is used in simplifying expressions, while the LCM is used in finding a common base in various situations.
In summary, while the GCF focuses on common factors, the LCM focuses on common multiples. Both concepts are important in different mathematical contexts and problem-solving scenarios.
The concept of the Greatest Common Factor (GCF) has various real-life applications in different fields. Here are some examples:
`1`. Sharing Resources: In resource allocation or distribution scenarios, finding the GCF can help determine the largest quantity that can be evenly distributed among different groups or individuals.
`2`. Design and Proportions: In design and architecture, finding the GCF is crucial for maintaining proportions and ensuring that elements are scaled appropriately. This is particularly important in fields like graphic design, where ratios play a significant role.
`3`. Manufacturing and Packaging: Industries that involve manufacturing and packaging often use the GCF to determine the most efficient way to package products. It helps find the largest common size or quantity that fits into various packaging options.
`4`. Time Management: When planning schedules or coordinating activities, finding the GCF of different time intervals can help identify the best times for common activities or events. This is particularly useful in event planning and project management.
`5`. Programming and Algorithms: In computer science, algorithms often involve finding the GCF to optimize processes and improve efficiency. For example, in scheduling tasks or allocating resources in software development.
`6`. Utilities and Infrastructure: In urban planning, the GCF may be used to determine the most efficient placement of utilities such as streetlights or waste bins, ensuring an even distribution throughout a neighborhood.
`7`. Mathematics Education: Teaching and learning about factors, multiples, and the GCF are fundamental in mathematics education. Understanding these concepts helps students solve problems and apply mathematical reasoning in various situations.
Example `1`. Find the Greatest Common Factor (GCF) of `35`, `40`, and `100` using the listing factors method.
Let's list the factors of `35`, `40`, and `100`:
- Factors of `35: 1, 5, 7, 35`
- Factors of `40: 1, 2, 4, 5, 8, 10, 20, 40`
- Factors of `100: 1, 2, 4, 5, 10, 20, 25, 50, 100`
Now, let's identify the common factors:
Common factors: `1, 5`
Therefore, the GCF`(35, 40, 100)` is `5`, as it is the largest number that divides all three numbers without leaving a remainder.
Example `2`. Find the GCF of `72` and `90`.
Let's list the factors of `72` and `90`:
- Factors of `72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72`
- Factors of `90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90`
Common factors: `1, 2, 3, 6, 9, 18`
GCF`(72, 90) = 18`
Example `3`. Find the GCF of `45` and `80`.
To find the Greatest Common Factor (GCF) of `45` and `80` using the division method (also known as the Euclidean Algorithm), follow these steps:
Step `1`: Divide the larger number by the smaller number.
`80 \div 45 = 1` with a remainder of `35`
Step `2`: Replace the larger number.
Replace the larger number `(80)` with the smaller number `(45)`, and replace the smaller number `(45)` with the remainder `(35)`.
`45 \div 35 = 1` with a remainder of `10`
Step `3`: Continue the process.
Continue the process until the remainder is zero.
`35 \div 10 = 3` with a remainder of `5` `10 \div 5 = 2` with a remainder of `0`
Step `4`: Identify the GCF.
The last non-zero remainder is `5`. Therefore, the GCF`(45, 80) = 5`.
So, using the division method, the GCF of `45` and `80` is `5`.
Example `4`. Find the GCF of `184`, `256`, and `388` by the prime factorization method.
To find the Greatest Common Factor (GCF) of `184`, `256`, and `388` using the prime factorization method, follow these steps:
Step `1`: Find the prime factorization of each number
- Prime factorization of `184`: \( 184 = 2^3 \times 23 \)
- Prime factorization of `256`: \( 256 = 2^8 \)
- Prime factorization of `388`: \( 388 = 2^2 \times 97 \)
Step `2`: Identify the common prime factors among the prime factorizations:
Common factors: \(2^2 = 4\)
Step `3`: Multiply the common prime factors
Multiply the common prime factors to find the GCF:
\( GCF(184, 256, 388) = 4 \)
Therefore, the GCF of `184`, `256`, and `388` is `4`.
Example `5`. What is the GCF of `300`, `45`, and `90`?
To find the Greatest Common Factor (GCF) of 300, 45, and 90, you can use the prime factorization method. Let's break down the prime factorization of each number:
- Prime factorization of `300`: \( 300 = 2^2 \times 3 \times 5^2 \)
- Prime factorization of `45`: \( 45 = 3^2 \times 5 \)
- Prime factorization of `90`: \( 90 = 2 \times 3^2 \times 5 \)
Now, identify the common prime factors:
Common factors: \( 3 \times 5 = 15 \)
Therefore, the GCF`(300, 45, 90)` is `15`.
Practice Problems
Q`1`. What is the GCF of `17`, `19` and `29`?
Q`2`. Find the Greatest Common Factor (GCF) of `84`, `72`, and `90`.
Q`3`. Find the Greatest Common Factor (GCF) of `1260` and `945`.
Q`4`. Find the Greatest Common Factor (GCF) of `324`, `468`, and `540`.
Q`5`. What is the GCF of `88`, `56`, and `120`?
Q`1`. How is the GCF denoted?
Answer: The GCF is often denoted as GCF`(a, b)`, where "`a`" and "`b`" are the numbers for which we want to find the greatest common factor.
Q`2`. How do you find the GCF of two numbers?
Answer: The GCF can be found by listing the factors of each number, identifying the common factors and picking the smallest amongst the common factors. Another method involves using prime factorization.
Q`3`. Can the GCF be larger than the smallest number?
Answer: No, the GCF cannot be larger than the smallest number. It is always less than or equal to the smallest number.
Q`4`. Can the GCF be negative?
Answer: No, the GCF is defined as a positive integer. It represents the largest positive number that divides the given numbers without leaving a remainder.
Q`5`. Is the GCF unique for any set of numbers?
Answer: Yes, the GCF is unique for any set of numbers. However, if all numbers are zero, the GCF is undefined.
Q`6`. How is the GCF used in simplifying fractions?
Answer: The GCF is used to simplify fractions by dividing both the numerator and denominator by their GCF. This results in an equivalent fraction in its simplest form.
Q`7`. What is the GCF of prime numbers?
Answer: The GCF of two or more prime numbers is always `1` because prime numbers have no common factors other than `1`.
Algebra - Order Of Operations Algebra - Distributive Property `X` And `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant
6.1 Greatest Common Factor and Factor by Grouping
Learning objectives.
By the end of this section, you will be able to:
- Find the greatest common factor of two or more expressions
- Factor the greatest common factor from a polynomial
- Factor by grouping
Be Prepared 6.1
Before you get started, take this readiness quiz.
Factor 56 into primes. If you missed this problem, review Example 1.2 .
Be Prepared 6.2
Find the least common multiple (LCM) of 18 and 24. If you missed this problem, review Example 1.3 .
Be Prepared 6.3
Multiply: −3 a ( 7 a + 8 b ) . −3 a ( 7 a + 8 b ) . If you missed this problem, review Example 5.26 .
Find the Greatest Common Factor of Two or More Expressions
Earlier we multiplied factors together to get a product . Now, we will reverse this process; we will start with a product and then break it down into its factors. Splitting a product into factors is called factoring .
We have learned how to factor numbers to find the least common multiple (LCM) of two or more numbers. Now we will factor expressions and find the greatest common factor of two or more expressions. The method we use is similar to what we used to find the LCM.
Greatest Common Factor
The greatest common factor (GCF) of two or more expressions is the largest expression that is a factor of all the expressions.
We summarize the steps we use to find the greatest common factor.
Find the greatest common factor (GCF) of two expressions.
- Step 1. Factor each coefficient into primes. Write all variables with exponents in expanded form.
- Step 2. List all factors—matching common factors in a column. In each column, circle the common factors.
- Step 3. Bring down the common factors that all expressions share.
- Step 4. Multiply the factors.
The next example will show us the steps to find the greatest common factor of three expressions.
Example 6.1
Find the greatest common factor of 21 x 3 , 9 x 2 , 15 x . 21 x 3 , 9 x 2 , 15 x .
| Factor each coefficient into primes and write the variables with exponents in expanded form. Circle the common factors in each column. Bring down the common factors. | |
| Multiply the factors. | |
| The GCF of , and is . |
Find the greatest common factor: 25 m 4 , 35 m 3 , 20 m 2 . 25 m 4 , 35 m 3 , 20 m 2 .
Find the greatest common factor: 14 x 3 , 70 x 2 , 105 x . 14 x 3 , 70 x 2 , 105 x .
Factor the Greatest Common Factor from a Polynomial
It is sometimes useful to represent a number as a product of factors, for example, 12 as 2 · 6 2 · 6 or 3 · 4 . 3 · 4 . In algebra, it can also be useful to represent a polynomial in factored form. We will start with a product, such as 3 x 2 + 15 x , 3 x 2 + 15 x , and end with its factors, 3 x ( x + 5 ) . 3 x ( x + 5 ) . To do this we apply the Distributive Property “in reverse.”
We state the Distributive Property here just as you saw it in earlier chapters and “in reverse.”
Distributive Property
If a , b , and c are real numbers, then
The form on the left is used to multiply. The form on the right is used to factor.
So how do you use the Distributive Property to factor a polynomial ? You just find the GCF of all the terms and write the polynomial as a product!
Example 6.2
How to use the distributive property to factor a polynomial.
Factor: 8 m 3 − 12 m 2 n + 20 m n 2 . 8 m 3 − 12 m 2 n + 20 m n 2 .
Factor: 9 x y 2 + 6 x 2 y 2 + 21 y 3 . 9 x y 2 + 6 x 2 y 2 + 21 y 3 .
Factor: 3 p 3 − 6 p 2 q + 9 p q 3 . 3 p 3 − 6 p 2 q + 9 p q 3 .
Factor the greatest common factor from a polynomial.
- Step 1. Find the GCF of all the terms of the polynomial.
- Step 2. Rewrite each term as a product using the GCF.
- Step 3. Use the “reverse” Distributive Property to factor the expression.
- Step 4. Check by multiplying the factors.
Factor as a Noun and a Verb
We use “factor” as both a noun and a verb:
Example 6.3
Factor: 5 x 3 − 25 x 2 . 5 x 3 − 25 x 2 .
| Find the GCF of and | ||
| Rewrite each term. | ||
| Factor the GCF. | ||
| Check: | ||
Factor: 2 x 3 + 12 x 2 . 2 x 3 + 12 x 2 .
Factor: 6 y 3 − 15 y 2 . 6 y 3 − 15 y 2 .
Example 6.4
Factor: 8 x 3 y − 10 x 2 y 2 + 12 x y 3 . 8 x 3 y − 10 x 2 y 2 + 12 x y 3 .
| The GCF of is | |
| Rewrite each term using the GCF, | |
| Factor the GCF. | |
| Check: |
Factor: 15 x 3 y − 3 x 2 y 2 + 6 x y 3 . 15 x 3 y − 3 x 2 y 2 + 6 x y 3 .
Factor: 8 a 3 b + 2 a 2 b 2 − 6 a b 3 . 8 a 3 b + 2 a 2 b 2 − 6 a b 3 .
When the leading coefficient is negative, we factor the negative out as part of the GCF.
Example 6.5
Factor: −4 a 3 + 36 a 2 − 8 a . −4 a 3 + 36 a 2 − 8 a .
The leading coefficient is negative, so the GCF will be negative.
| Rewrite each term using the GCF, | |
| Factor the GCF. | |
| Check: |
Factor: −4 b 3 + 16 b 2 − 8 b . −4 b 3 + 16 b 2 − 8 b .
Try It 6.10
Factor: −7 a 3 + 21 a 2 − 14 a . −7 a 3 + 21 a 2 − 14 a .
So far our greatest common factors have been monomials. In the next example, the greatest common factor is a binomial.
Example 6.6
Factor: 3 y ( y + 7 ) − 4 ( y + 7 ) . 3 y ( y + 7 ) − 4 ( y + 7 ) .
The GCF is the binomial y + 7 . y + 7 .
| Factor the GCF, | |
| Check on your own by multiplying. |
Try It 6.11
Factor: 4 m ( m + 3 ) − 7 ( m + 3 ) . 4 m ( m + 3 ) − 7 ( m + 3 ) .

Try It 6.12
Factor: 8 n ( n − 4 ) + 5 ( n − 4 ) . 8 n ( n − 4 ) + 5 ( n − 4 ) .
Factor by Grouping
Sometimes there is no common factor of all the terms of a polynomial. When there are four terms we separate the polynomial into two parts with two terms in each part. Then look for the GCF in each part. If the polynomial can be factored, you will find a common factor emerges from both parts. Not all polynomials can be factored. Just like some numbers are prime , some polynomials are prime.
Example 6.7
How to factor a polynomial by grouping.
Factor by grouping: x y + 3 y + 2 x + 6 . x y + 3 y + 2 x + 6 .
Try It 6.13
Factor by grouping: x y + 8 y + 3 x + 24 . x y + 8 y + 3 x + 24 .
Try It 6.14
Factor by grouping: a b + 7 b + 8 a + 56 . a b + 7 b + 8 a + 56 .
Factor by grouping.
- Step 1. Group terms with common factors.
- Step 2. Factor out the common factor in each group.
- Step 3. Factor the common factor from the expression.
Example 6.8
Factor by grouping: ⓐ x 2 + 3 x − 2 x − 6 x 2 + 3 x − 2 x − 6 ⓑ 6 x 2 − 3 x − 4 x + 2 . 6 x 2 − 3 x − 4 x + 2 .
| There is no GCF in all four terms. | |
| Separate into two parts. | |
| Factor the GCF from both parts. Be careful with the signs when factoring the GCF from the last two terms. | |
| Factor out the common factor. | |
| Check on your own by multiplying. |
| There is no GCF in all four terms. | |
| Separate into two parts. | |
| Factor the GCF from both parts. | |
| Factor out the common factor. | |
| Check on your own by multiplying. |
Try It 6.15
Factor by grouping: ⓐ x 2 + 2 x − 5 x − 10 x 2 + 2 x − 5 x − 10 ⓑ 20 x 2 − 16 x − 15 x + 12 . 20 x 2 − 16 x − 15 x + 12 .
Try It 6.16
Factor by grouping: ⓐ y 2 + 4 y − 7 y − 28 y 2 + 4 y − 7 y − 28 ⓑ 42 m 2 − 18 m − 35 m + 15 . 42 m 2 − 18 m − 35 m + 15 .
Section 6.1 Exercises
Practice makes perfect.
In the following exercises, find the greatest common factor.
10 p 3 q , 12 p q 2 10 p 3 q , 12 p q 2
8 a 2 b 3 , 10 a b 2 8 a 2 b 3 , 10 a b 2
12 m 2 n 3 , 30 m 5 n 3 12 m 2 n 3 , 30 m 5 n 3
28 x 2 y 4 , 42 x 4 y 4 28 x 2 y 4 , 42 x 4 y 4
10 a 3 , 12 a 2 , 14 a 10 a 3 , 12 a 2 , 14 a
20 y 3 , 28 y 2 , 40 y 20 y 3 , 28 y 2 , 40 y
35 x 3 y 2 , 10 x 4 y , 5 x 5 y 3 35 x 3 y 2 , 10 x 4 y , 5 x 5 y 3
27 p 2 q 3 , 45 p 3 q 4 , 9 p 4 q 3 27 p 2 q 3 , 45 p 3 q 4 , 9 p 4 q 3
In the following exercises, factor the greatest common factor from each polynomial.
6 m + 9 6 m + 9
14 p + 35 14 p + 35
9 n − 63 9 n − 63
45 b − 18 45 b − 18
3 x 2 + 6 x − 9 3 x 2 + 6 x − 9
4 y 2 + 8 y − 4 4 y 2 + 8 y − 4
8 p 2 + 4 p + 2 8 p 2 + 4 p + 2
10 q 2 + 14 q + 20 10 q 2 + 14 q + 20
8 y 3 + 16 y 2 8 y 3 + 16 y 2
12 x 3 − 10 x 12 x 3 − 10 x
5 x 3 − 15 x 2 + 20 x 5 x 3 − 15 x 2 + 20 x
8 m 2 − 40 m + 16 8 m 2 − 40 m + 16
24 x 3 − 12 x 2 + 15 x 24 x 3 − 12 x 2 + 15 x
24 y 3 − 18 y 2 − 30 y 24 y 3 − 18 y 2 − 30 y
12 x y 2 + 18 x 2 y 2 − 30 y 3 12 x y 2 + 18 x 2 y 2 − 30 y 3
21 p q 2 + 35 p 2 q 2 − 28 q 3 21 p q 2 + 35 p 2 q 2 − 28 q 3
20 x 3 y − 4 x 2 y 2 + 12 x y 3 20 x 3 y − 4 x 2 y 2 + 12 x y 3
24 a 3 b + 6 a 2 b 2 − 18 a b 3 24 a 3 b + 6 a 2 b 2 − 18 a b 3
−2 x − 4 −2 x − 4
−3 b + 12 −3 b + 12
−2 x 3 + 18 x 2 − 8 x −2 x 3 + 18 x 2 − 8 x
−5 y 3 + 35 y 2 − 15 y −5 y 3 + 35 y 2 − 15 y
−4 p 3 q − 12 p 2 q 2 + 16 p q 2 −4 p 3 q − 12 p 2 q 2 + 16 p q 2
−6 a 3 b − 12 a 2 b 2 + 18 a b 2 −6 a 3 b − 12 a 2 b 2 + 18 a b 2
5 x ( x + 1 ) + 3 ( x + 1 ) 5 x ( x + 1 ) + 3 ( x + 1 )
2 x ( x − 1 ) + 9 ( x − 1 ) 2 x ( x − 1 ) + 9 ( x − 1 )
3 b ( b − 2 ) − 13 ( b − 2 ) 3 b ( b − 2 ) − 13 ( b − 2 )
6 m ( m − 5 ) − 7 ( m − 5 ) 6 m ( m − 5 ) − 7 ( m − 5 )
In the following exercises, factor by grouping.
a b + 5 a + 3 b + 15 a b + 5 a + 3 b + 15
c d + 6 c + 4 d + 24 c d + 6 c + 4 d + 24
8 y 2 + y + 40 y + 5 8 y 2 + y + 40 y + 5
6 y 2 + 7 y + 24 y + 28 6 y 2 + 7 y + 24 y + 28
u v − 9 u + 2 v − 18 u v − 9 u + 2 v − 18
p q − 10 p + 8 q − 80 p q − 10 p + 8 q − 80
u 2 − u + 6 u − 6 u 2 − u + 6 u − 6
x 2 − x + 4 x − 4 x 2 − x + 4 x − 4
9 p 2 + 12 p − 15 p − 20 9 p 2 + 12 p − 15 p − 20
16 q 2 + 20 q − 28 q − 35 16 q 2 + 20 q − 28 q − 35
m n − 6 m − 4 n + 24 m n − 6 m − 4 n + 24
r 2 − 3 r − r + 3 r 2 − 3 r − r + 3
2 x 2 − 14 x − 5 x + 35 2 x 2 − 14 x − 5 x + 35
4 x 2 − 36 x − 3 x + 27 4 x 2 − 36 x − 3 x + 27
Mixed Practice
In the following exercises, factor.
−18 x y 2 − 27 x 2 y −18 x y 2 − 27 x 2 y
−4 x 3 y 5 − x 2 y 3 + 12 x y 4 −4 x 3 y 5 − x 2 y 3 + 12 x y 4
3 x 3 − 7 x 2 + 6 x − 14 3 x 3 − 7 x 2 + 6 x − 14
x 3 + x 2 + x + 1 x 3 + x 2 + x + 1
x 2 + x y + 5 x + 5 y x 2 + x y + 5 x + 5 y
5 x 3 − 3 x 2 + 5 x − 3 5 x 3 − 3 x 2 + 5 x − 3
Writing Exercises
What does it mean to say a polynomial is in factored form?
How do you check result after factoring a polynomial?
The greatest common factor of 36 and 60 is 12. Explain what this means.
What is the GCF of y 4 , y 5 , y 4 , y 5 , and y 10 ? y 10 ? Write a general rule that tells you how to find the GCF of y a , y b , y a , y b , and y c . y c .
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ If most of your checks were:
…confidently. Congratulations! You have achieved your goals in this section! Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific!
…with some help. This must be addressed quickly as topics you do not master become potholes in your road to success. Math is sequential - every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Whom can you ask for help?Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no - I don’t get it! This is critical and you must not ignore it. You need to get help immediately or you will quickly be overwhelmed. See your instructor as soon as possible to discuss your situation. Together you can come up with a plan to get you the help you need.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
- Authors: Lynn Marecek, Andrea Honeycutt Mathis
- Publisher/website: OpenStax
- Book title: Intermediate Algebra 2e
- Publication date: May 6, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
- Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/6-1-greatest-common-factor-and-factor-by-grouping
© Jul 24, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation.
GREATEST COMMON FACTOR WORD PROBLEMS
Problem 1 :
Find the greatest possible length that can be used to measure exactly the lengths 84 feet, 98 feet and 126 feet.
The greatest possible length that can be used to measure the given lengths is the greatest common factor of 84, 63 and 97.
Find the greatest common factor of 84, 98 and 126.
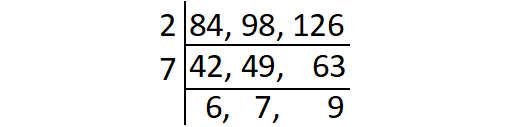
Product of common factors of 84, 98 and 126 is
GCF (84, 98, 126) = 14.
The greatest possible length that can be used to measure the given lengths is 14 feet.
Problem 2 :
A warehouse has three shelves that can hold 8, 12, or 16 skateboards. Each shelf has sections holding the same number of skateboards. What is the greatest number of skateboards that can be put in a section? Explain
Write the factors of 8, 12 and 16.
8 = 1, 2, 4 , 8
12 = 1, 2, 3, 4 , 6, 12
16 = 1, 2, 4 , 8, 16
The greatest common factor of 8, 12 and 16 is 4.
So, the greatest number of skateboards can be put in a section is 4.
Problem 3 :
Lily has 15 oranges, 9 peaches, and 18 pears. She wants to put all of the fruit into decorative baskets. Each basket must have the same number of pieces of fruit in it. Without mixing fruits, what is the greatest number of pieces of fruit Lily can put in each basket? Explain.
Write the factors of 15, 9 and 18.
15 = 1, 2, 3 , 5, 15
9 = 1, 3 , 9
18 = 1, 2, 3 , 6, 9, 18
The greatest common factor of 15, 9 and 18 is 3.
So, the greatest number of pieces of fruit Lily can put in each basket is 3.
Problem 4 :
A store has 120 lbs and 250 lbs of two kinds of meat. The store wants to sell the meat by filling the two kinds in boxes of equal volumes and no meat left over. Find the greatest volume of such a box.
The given two quantities 120 and 250 can be divided by 2, 5, 10,... exactly. That is, both kinds of meat can be sold in boxes of equal volume of 2, 5, 10,...
But, the volume of meat filled in boxes must be greatest.
So, we have to find the largest number which exactly divides 120 and 250. That is the highest common factor (HCF) of 120 and 250.
HCF (120, 250) = 10
The 1 st kind 120 lbs is sold in 12 boxes of volume 10 lbs in each box.
The 2 nd kind 250 lbs is sold in 25 boxes of volume 10 lbs in each box.
Hence, the greatest volume of the box is 10 lbs.
Problem 5 :
Two numbers are in the ratio 2 : 3. If the second number is 27, find their greatest common factor.
Because the two numbers are in the ratio 2 : 3, the numbers can be assumed as 2x and 3x.
Find the greatest common multiple of 2x and 3x.
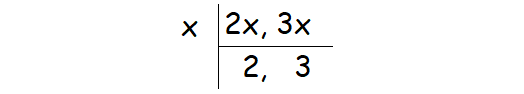
The common factor of 2x and 3x is x.
Greatest common factor (2x, 3x) = x
But, it is given that the second number is 27.
Divide each side by 3.
So, the greatest factor of the two numbers is 9.
Problem 6 :
Two numbers are in the ratio 3 : 5 and their greatest common factor is 18 . Find the numbers.
Because the two numbers are in the ratio 3 : 5, the numbers can be assumed as 3x and 5x.
Greatest common factor (3x, 5x) = x
But, it is given that the greatest common factor of the two numbers is 18.
Substitute x = 18 in 3x and 5x.
3x = 3(18) = 54
5x = 5(18) = 90
So, the two numbers are 54 and 90.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Honors algebra 2 problems with solutions (part - 1).
Aug 09, 24 08:39 PM
Honors Algebra 2 Problems with Solutions (Part - 2)
Aug 09, 24 08:36 PM
SAT Math Resources (Videos, Concepts, Worksheets and More)
Aug 09, 24 06:15 AM

Reading & Math for K-5
- Kindergarten
- Learning numbers
- Comparing numbers
- Place Value
- Roman numerals
- Subtraction
- Multiplication
- Order of operations
- Drills & practice
- Measurement
- Factoring & prime factors
- Proportions
- Shape & geometry
- Data & graphing
- Word problems
- Children's stories
- Leveled Stories
- Sentences & passages
- Context clues
- Cause & effect
- Compare & contrast
- Fact vs. fiction
- Fact vs. opinion
- Main idea & details
- Story elements
- Conclusions & inferences
- Sounds & phonics
- Words & vocabulary
- Reading comprehension
- Early writing
- Numbers & counting
- Simple math
- Social skills
- Other activities
- Dolch sight words
- Fry sight words
- Multiple meaning words
- Prefixes & suffixes
- Vocabulary cards
- Other parts of speech
- Punctuation
- Capitalization
- Narrative writing
- Opinion writing
- Informative writing
- Cursive alphabet
- Cursive letters
- Cursive letter joins
- Cursive words
- Cursive sentences
- Cursive passages
- Grammar & Writing
Breadcrumbs
- Word Problems
- GCF & LCM

Download & Print From only $2.60
GCF and LCM word problems
Factors and multiples.
These word problems need the use of greatest common factors (GCFs) or least common multiples (LCMs) to solve. Mixing GCF and LCM word problems encourages students to read and think about the questions, rather than simply recognizing a pattern to the solutions.

These worksheets are available to members only.
Join K5 to save time, skip ads and access more content. Learn More
More word problem worksheets
Explore all of our math word problem worksheets , from kindergarten through grade 5.
What is K5?
K5 Learning offers free worksheets , flashcards and inexpensive workbooks for kids in kindergarten to grade 5. Become a member to access additional content and skip ads.
Our members helped us give away millions of worksheets last year.
We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.
Members skip ads and access exclusive features.
Learn about member benefits
This content is available to members only.
- Forgot Password?
- School Guide
- Mathematics
- Number System and Arithmetic
- Trigonometry
- Probability
- Mensuration
- Maths Formulas
- Integration Formulas
- Differentiation Formulas
- Trigonometry Formulas
- Algebra Formulas
- Mensuration Formula
- Statistics Formulas
- Trigonometric Table
Greatest Common Factor
Greatest Common Factor or GCF is the largest positive integer that evenly divides two or more integers without leaving a residual. In simple words, the Greatest Common Factor is the largest value that can be used to divide these numbers and get whole numbers.
Greatest Common Factor is a fundamental idea in mathematics and is essential for equation solving, simplifying fractions, and finding common components in a variety of mathematical settings.
In this article, we will discuss the concept of the Greatest Common Factor in detail including definition, methods to find the Greatest Common Factor , and various solved examples for calculating the Greatest Common Factor .

Table of Content
What is Greatest Common Factor?
How to find the greatest common factor, examples of greatest common factor, lcm and gcf.
The largest number that divides two or more integers without leaving a remainder is known as the Greatest Common Factor (GCF) and it is also referred to as the Greatest Common Divisor (GCD) or Highest Common Factor (HCF). The GCF is essential for reducing difficult mathematical statements and has applications in number theory, cryptography, and computer science.
Greatest Common Factor Definition
The Greatest Common Factor (GCF) is the greatest positive integer that evenly divides two or more integers without leaving a remainder.
Greatest Common Factor is a fundamental mathematical idea used to simplify fractions and solve algebraic problems. One approach for determining the GCF is prime factorization, which involves identifying the prime factors of each integer and multiplying the common factors with the largest exponent together. The Euclidean algorithm, which includes consecutive division until the remainder reaches zero, is another option.

The two methods for determining the biggest common factor between two integers are as follows:
- Listing out Common Factors
- Prime Factorization
- Division Method
Greatest Common Factor by Listing Out Common Factors
This technique is methodically noting and contrasting the components of two or more integers in order to get the Greatest Common Factor (GCF). To divide all the supplied numbers without leaving a remainder, the factors of each number are determined and then compared to get the greatest positive integer. For small or relatively simple groups of integers, this method offers a simple technique to identify the largest common divisor that the numbers share.
Let’s determine the two numbers 48 and 60’s greatest common factor (GCF) by systematically listing each of their common factors.
Step 1: Write down each number’s components in order. Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 Step 2: Find the elements that both numbers have in common. Common factors: 1, 2, 3, 4, 6, 12 Step 3: Determine the largest common factor. The largest common factor is 12. The greatest common factor (GCF) between 48 and 60 is 12.
In this case, we enumerated the factors of both numbers, located the ones that they have in common, and discovered that the biggest one is 12. By methodically listing each pair of numbers’ elements and finding the shared factors, it is possible to use this approach to get the GCF of any two numbers.
Greatest Common Factor by Prime Factorization
The GCF of two or more integers is calculated using this approach by first locating their prime factorizations. The numbers are divided into their prime components, and the most prevalent prime components with the smallest exponents are then determined. The GCF of the given numbers is obtained by adding these frequent prime factors. This method makes use of the inherent qualities of prime numbers to find the biggest common divisor shared by the numbers, which is particularly helpful for bigger numbers.
Let’s use the prime factorization technique to get the GCF of two integers, 84 and 108. the following steps:
Step 1: Determine each number’s prime factors. Prime factorization of 84: 2 x 2 x 3 x 7 Prime factorization of 108: 2 x 2 x 3 x 3 x 3 Step 2: List the common prime factors and their exponents with the lowest values. Common prime factors: 2 x 2 x 3 Step 3: Determine the common prime factors’ product. 2 x 2 x 3 = 12
The GCF (Greatest Common Factor) of 84 and 108 is 12, which is the result.
Greatest Common Factor by Division Method
The division method is a mathematical approach that is used to calculate the Greatest Common Factor (GCF) of two or more integers. It entails a methodical procedure of splitting data and determining common components. Starting with the supplied integers, divide them one by one, using the residual of each division as the new divisor. This technique is repeated until a remainder of zero is obtained. The GCF is the divisor at this point.
Step 1: Write down the numbers you want to find the GCF of. For example, let’s find the GCF of 24 and 36: Step 2: Find the prime factors of each number. Prime factors of 24: 2 x 2 x 2 x 3 Prime factors of 36: 2 x 2 x 3 x 3 Step 3: Identify the common prime factors among all the numbers. Common prime factor of 24 = 2 3 * 3 Common prime factor of 36 = 2 2 * 3 2 Step 4: Take the lowest exponent for each common prime factor. If a prime factor doesn’t appear in all the numbers, it’s not considered. Common factors: 2 2 and 3 Step 5: Multiply all the common prime factors using the lowest exponent found in step 4. GCF = 2 2 * 3 = 12.
After finding the Greatest Common Factor (GCF) using the division method, it’s essential to apply the result appropriately. The GCF is an important component in simplifying fractions, calculating equations, and dealing with various mathematical issues, streamlining complicated computations.
There are various examples we can consider for calculation of Greatest Common Factor. Let’s consider the following examples.
Greatest Common Factor of 12 and 18
Let’s find the GCF of 12 and 18. Factors of 12 = 1, 2, 3, 4, 6, 12 Factors of 18 = 1, 2, 3, 6, 9, 18 Between 12 and 18, 6 is the greatest common number. Considering that all number factors may be found between 1 and 6. The number 6 is by far the larger of these two numbers. Thus, these integers have a GCF of 6.
Greatest Common Factor of 24 and 40
The numbers 24 and 40 are provided. We’ll determine each of these numbers’ components. Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24 Factors of 40 = 1, 2, 4, 5, 8, 10, 20, 40 In this case, the common factors for the numbers 24 and 40 are 1, 2, 4, and 8. The greatest common factor among all of these is 8, hence GCF(24 and 40) = 8.
Greatest Common Factor of 15 and 20
Prime factors of 15: 1, 3, 5, 15 Prime factors of 20: 1, 2, 4, 5, 10, 20 In this case, the common factors for the numbers 15 and 20 are 1 and 5. The greatest common factor among all of these is 5, hence GCF(15 and 20) = 5.
Greatest Common Factor of Monomial
The highest word that divides two or more monomials without remainder is the greatest common factor (GCF). Finding the biggest word that splits equally into two or more monomials is the Greatest Common Factor (GCF) of monomials.
For example, take the monomials 6x 2 y and 8xy 3 :
Step 1: Determine the prime factors of each coefficient and variable term . The prime factors for 6x 2 y are 2, 3, x 2 , and y. The prime factors for 8xy 3 are 2, 2, 2, x, y 3 . Step 2: Find the common factors. The common factors in this situation are 2, x, and y. Step 3: Find the exponent with the lowest exponent for each common factor. It’s x 1 and y 1 in this case. Step 4: Divide the common components by the lowest exponent: 2xy.
As a result, the GCF of 6x 2 y and 8xy 3 is 2xy. This GCF is essential for simplifying monomial expressions and factoring polynomial expressions.
Understanding the concepts of Least Common Multiple (LCM) and Greatest Common Factor (GCF) is essential in mathematics. These two principles are essential in many mathematical procedures and problem solutions. Let’s look at the division method used to determine the GCF and how it helps with fractions and equations.
| Aspect | Least Common Multiple (LCM) | Greatest Common Factor (GCF) |
|---|---|---|
| Definition | The least positive multiple that two or more numbers have in common. | The most positive divisor that two or more integers can share. |
| Objective | Used in a variety of situations to determine the smallest common multiple. | Used in a variety of situations to determine the biggest common divisor. |
| Calculation | Involves figuring out the usual multiples and choosing the least one. | Involves finding frequent divisors and picking the biggest one. |
| Properties | Always larger than or equal to the provided numbers is the LCM. | Always, the GCF is less than or equal to the specified values. |
- HCF and LCM
- HCF and LCM Questions
- Whole numbers
- Factorization of Polynomials
Solved Examples of Greatest Common Factor
Example 1: Find the Greatest Common Factor (GCF) of 15, 25 and 35.
Factors of 15, 25 and 35 are as follows: Factors of 15 = 1, 3, 5, 15 Factors of 25 = 1, 5, 25 Factors of 35 = 1, 5, 7, 35 Between 15, 25 and 35, 5 is the greatest common number. Considering that all number factors may be found between 1 and 5. The number 5 is by far the larger of these two numbers. Thus, these integers have a GCF of 5.
Example 2: Using the approach of listing factors, determine the GCF of 8, 16, and 32.
The numbers 8, 16, and 32 are provided. We’ll determine each of these numbers’ components. Factors of 8 = 1, 2, 4, 8 Factors of 16 = 1, 2, 4, 8, 16 Factors of 32 = 1, 2, 4, 8, 16, 32 In this case, the common factors for the numbers 8, 16, and 32 are 1, 2, 4, and 8. The greatest common factor among all of these is 8, hence GCF(8,16,32) = 8.
Example 3: By using the prime factorization technique, determine the GCF for 80, 120, and 160.
The numbers 80, 120, and 160 are provided. We will determine how many prime factors each of these integers has. Factors of 80 = 2 x 2 x 2 x 2 x 5 Factors of 120 = 2 x 2 x 2 x 3 x 5 Factors of 160 = 2 x 2 x 2 x 2 x 2 x 5 GCF of 80, 120 and 160 = 2 x 2 x 2 x 5 = 40 GCF (80,120,160) = 2 x 2 x 2 x 5 as a result. The sum of the common prime factors of these three numbers will result in the GCF of these three numbers. GCF of 80, 120 and 160 hence equals 2 x 2 x 2 x 5 = 40.
Practice Problems on Greatest Common Factor
Problem 1: Find the GCF of 12 and 18.
Problem 2: Calculate the GCD of 24 and 36.
Problem 3: Determine the GCF of 48, 60, and 84.
Problem 4: Find the greatest common factor of 35 and 49.
Problem 5: Compute the GCD of 72 and 90.
Problem 6: What is the GCF of 15 and 25?
Problem 7: Find the GCF of 16, 24, and 32.
Problem 8: Calculate the greatest common factor of 56 and 64.
Problem 9: Determine the GCD of 120 and 150.
Problem 10: Find the GCF of 9, 15, and 21.
Greatest Common Factor – FAQs
What is “greatest common factor” (gcf).
The greatest common factor, or GCF, is the largest number among all the common factors of two or more numbers. The GCF is the biggest number that divides the provided two numbers for any two numbers.
What is the mathematical concept of the Greatest Common Factor?
Simplifying fractions, factoring algebraic expressions, resolving equations, and identifying common divisors all depend on the greatest common factor. It’s an essential idea that serves as the foundation for many mathematical operations and simplification methods.
What is the greatest common factor of 36 and 48?
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36. The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48. The common factors of 36 and 48 are 1, 2, 3, 4, 6, and 12. As a result, the GCF for 36 and 48 is 12.
How does prime factorization relate to the GCF?
A number is expressed as the product of its prime components through the process of prime factorization. Finding the common prime factors with the lowest exponents from the prime factorizations of two or more integers yields the GCF of those numbers.
What is the greatest common factor of 54 and 36?
The factors of 54 are 1, 2, 3, 6, 9, 18, 27 and 54. The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36. The common factors of 54 and 36 are 1, 2, 3, 6, 9 and 18. As a result, the GCF for 54 and 36 is 18.
Can a GCF exist for negative numbers?
Positive numbers can indeed have a GCF. The method used to determine the GCF for negative integers is the same as it is for positive values. For factorization, the numbers’ absolute values are taken into account, and the GCF is calculated in accordance with this.
Is GCF larger than LCM?
The LCM is the smallest common multiple of the supplied numbers that can be divided by both, whereas the GCF is the greatest common factor of the given numbers that can be divided by both. Thus, the LCM of any two numbers is bigger than the GCF of the numbers.
How do You Find the Greatest Common Factor?
To find the greatest common factor (GCF) of two or more numbers, list their factors and identify the largest number that divides them all evenly.
What is the GCF of 12 and 18?
The greatest common factor (GCF) of 12 and 18 is 6.
Is GCD and HCF Same?
Yes, GCD (Greatest Common Divisor) and HCF (Highest Common Factor) refer to the same mathematical concept and can be used interchangeably. They both represent the largest number that divides two or more integers without leaving a remainder.
Please Login to comment...
Similar reads.
- Geeks Premier League
- School Learning
- Geeks Premier League 2023
- Math-Concepts
- Maths-Class-6
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Course: 6th grade > Unit 6
- Greatest common factor examples
Greatest common factor explained
- Greatest common factor
- Factor with the distributive property
- Factor with the distributive property (no variables)
- Greatest common factor review
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Video transcript
GCF, Distributive Property (Grade 6)
In these lessons, Grade 6 students learn to find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12.
Related Pages Greatest Common Factor Number Properties Common Core for Grade 6 Grade 6 Math
Use the distributive property to express a sum of two whole numbers 1–100 with a common factor as a multiple of a sum of two whole numbers with no common factor.
For example, express 36 + 8 as 4 (9 + 2).
Common Core: 6.NS.4
Suggested Learning Targets
- I can find the greatest common factor and least common multiple.
- I can use the distributive property for whole numbers with no common factor.
- I can apply the Distributive Property to rewrite addition problems by factoring out the Greatest Common Factor.
Component Skills from Previous Grades
| Apply properties of operations as strategies to multiply and divide. For example, write 8 × 7 as 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Distributive property.) | Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. |
The following diagram shows how to use the GCF and Distributive Property to find the sum of two numbers. Scroll down the page for more examples and solutions on GCF and distributive property.
Greatest Common Factor (GCF)
How to find GCF
GCF and Distributive Property
6NS4 - Distributive Property
Example: 3(2 + 6)
6NS4 - Multiple of a Sum
How to write a sum of two whole numbers as a multiple of a sum of two whole numbers?
Example: Use the GCF and the distributive property to express a sum as a product. 20 + 35
Example: Use the GCF and the Distributive Property to express the sum as a product 18 + 27
GCF and the Distributive Property
Step 1: Find the GCF of the 2 numbers Step 2: Re-write using the distributive property.
Example: Use the GCF and the Distributive Property to express the sum. 36 + 8 27 + 18 25 + 60
Example: Apply the distributive property to the algebraic expression. 24x + 18y 10x + 15 16x + 32y
GCF And Distributive Property Word Problems
Learn how to use solve problems using the GCF and Distributive Property
Example: Bryan is setting chairs for a graduation ceremony. He has 50 black chairs and 60 white chairs. Each row will have the same number of chairs and and each row will have the same color chair. What is the greatest number of chairs that he can fit in each row? How many rows of each color chair will there be?
Use the GCF and Distributive Property to solve word problems
Example: A store clerk is bagging spices. He has 18 teaspoons of cinnamon and 30 teaspoons of nutmeg. Each bag need to contain the same number of teaspoons and each bag can contain only one spice. How many teaspoons of spice should the clerk put in each bag? How many bags of each spice would there be?
GCF and Distributive Property Problem Solving
Learn how to use the GCF in problem solving. Distinguish how to use the distributive property in problem solving.
Example: Madison has 56 roses and 42 daisies to use in floral centerpieces for a party. Each centerpiece will have the same number of flowers and will contain only roses or only daisies. What is the greatest number of flowers that Madison can use in each centerpiece?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
- Math Article
Greatest Common Factor

In Mathematics, a factor is a number which when multiplied by other numbers to get the desired numbers. The resulting number is also known as factors. Usually, the numbers can be factored into different combinations. The factors can be easily figured out if you are familiar with the multiplication tables . Here, we are going to discuss what is the greatest common factor, and how to find GCF with examples.
What is the Greatest Common Factor?
The largest number, which is the factor of two or more number is called the Greatest Common Factor (GCF). It is the largest number (factor) that divide them resulting in a Natural number. Once all the factors of the number are found, there are few factors which are common in both. The largest number that is found in the common factors is called the greatest common factor. The GCF is also known as the Highest Common Factor (HCF)
Let us consider the example given below:

For example – The GCF of 18, 21 is 3. Because the factors of the number 18 and 21 are:
Factors of 18 = 2 ×9 = 2 × 3 × 3
Factors of 21 = 3 ×7
Here, the number 3 is common in both the factors of numbers. Hence, the greatest common factor of 18 and 21 is 3.
Similarly, the GCF of 10, 15 and 25 is 5.
How to Find the Greatest Common Factor?
If we have to find out the GCF of two numbers, we will first list the prime factors of each number. The multiple of common factors of both the numbers results in GCF. If there are no common prime factors, the greatest common factor is 1.
Finding the GCF of a given number set can be easy. However, there are several steps need to be followed to get the correct GCF. In order to find the greatest common factor of two given numbers, you need to find all the factors of both the numbers and then identify the common factors.
Find out the GCF of 18 and 24
Prime factors of 18 – 2 × 3 × 3
Prime factors of 24 – 2 × 2 × 2 × 3
They have factors 2 and 3 in common so, thus G.C.F of 18 and 24 is 2 × 3 = 6
Also, try: GCF calculator
GCF and LCM
Greatest Common Factor of two or more numbers is defined as the largest number that is a factor of all the numbers.
Least Common Multiple of two or more numbers is the smallest number (non-zero) that is a multiple of all the numbers.
Factoring Greatest Common Factor
Factor method is used to list out all the prime factors, and you can easily find out the LCM and GCF. Factors are usually the numbers that we multiply together to get another number.
Example- Factors of 12 are 1,2,3,4,6 and 12 because 2 × 6 =12, 4 × 3 = 12 or 1 × 12 = 12. After finding out the factors of two numbers, we need to circle all the numbers that appear in both the list.
Greatest Common Factor Examples
Find the greatest common factor of 18 and 24.
First list all the factors of the given numbers.
Factors of 18 = 1, 2, 3, 6, 9 and 18
Factors of 24 = 1, 2, 3, 4, 6, 8, 12 and 24
The largest common factor of 18 and 24 is 6.
Thus G.C.F. is 6.
Find the GCF of 8, 18,28 and 48.
Factors are as follows-
Factors of 8 = 1, 2, 4, 8
Factors of 18 = 1, 2, 3, 6, 9, 18
Factors of 28 = 1, 2, 4, 7, 14, 28
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
The largest common factor of 8, 18, 28, 48 is 2. Because the factors 1 and 2 are found all the factors of numbers. Among these two numbers, the number 2 is the largest numbers. Hence, the GCF of these numbers is 2.
Stay tuned with BYJU’S – The Learning App and also visit www.byjus.com to get more Maths-related concepts to learn with ease.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below
Request OTP on Voice Call
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
- Sixth Grade lessons
- How to find the GCF and the LCM word problems
" class="arrow-title-img"> How to find the GCF and the LCM word problems
This enriching resource on how to find the GCF and LCM word problems is here to improve your kids' technical skills and performance in solving word problems efficiently.
Also, we will include effective problem-solving and instructional working strategies so that learners can easily tackle word problems concerning GCF and LCM. With this, your kids can wave goodbye to all the substantial challenges they face or encounter in solving math word problems.
In fact, with this resource, kids can easily identify the problem type and translate the problem into a solvable mathematical equation, thereby providing an accurate result for the word problem.
Steps on how to find the GCF and LCM word problems
Your kids will be excited as they discover simple steps on how to find the GCF and LCM word problems . These steps will model and help young learners easily identify the relational statements in any word problem they encounter. We will begin by designing easy rules to find GCF /LCM.
Also, our resource will guide your kids through identifying key problem features in word problems concerning HCF/LCM. And how to transform math problems into meaningful maths equation.
As we know, learning with examples is usually a great lesson for kids. Hence, this resource will present real-life situation examples to demonstrate how these steps work
Step 1: IDENTIFY:
- You have to start by reading the whole word problem very carefully.
- Then, figure out the scenario that the problem needs you to tackle.
- Last but not least, use the keywords found in the word problem to help you identify the operation you are supposed to carry out efficiently.
Speaking of keywords:
- When looking for GCF in a word problem, these are some of the general keywords you'll come across in the word problem: - greatest, largest, maximum, highest, etc.
- Another clue to know if you need to find the GCF in a word problem is when the problem presents itself as "groups," "rows," "sections," "how many sets," "divided into equal groups," "identical" "split," "share equally" "same combination," "same" "even amount," etc.
- When finding the LCM , these are some general keywords that you'll find in the word problem: - least, minimum, smallest, lowest, etc.
- Similarly, other clues to know if you are going to find but the LCM in a word problem is when the problem presents itself as an event that will repeat itself , when you find the word "every…" in the word problem, etc.
- ***One key Element for learners to understand is that they should not always rely on keywords alone . That is to say; the same keyword can have different meanings in different word problems .
- For this reason, we reiterate on the importance of reading the question very carefully to understand the situation that the word problem is describing , then figure out exactly which operation to use***
Step 2: STRATEGIZE:
At this stage, you should ask yourself, "how am I going to solve the problem?"
- You already know that, from the keyword(s) in the word problem, you will know if you need to look for the LCM or GCF .
- However, you don't have to depend entirely on keywords . Always try to understand the situation that the problem is describing very well before you start solving it.
- After knowing which operation you will perform, construct short expressions/sentences representing the given word problem.
Step 3: SET UP:
Now, write down a numerical expression representing the information given in the word problem.
Step 4: PROVIDE A SOLUTION:
From step 3 above,
If the word problem needs you to find the GCF , use any of the methods listed below:
- The factor tree and column method,
- The slide method,
- The prime factor method.
If the word problem needs you to find the LCM , use one of the following methods:
- Listing the multiples method,
- Prime factorization method,
- Division method,
- The factor tree and column method.
Step 5: CHECK YOUR WORK:
Finally, ask yourself this question. "Does my answer make sense?" If "YES," you are done. If "NO," go back to step 1 and start all over again.
You can always do this by solving to prove your answer, as shown in the attached example below.

Find more practices with these tests online
- Greatest common factor word problems
- Lowest common multiple word problems
- number theory
GCF and LCM word problems

Convert between standard and scientic notation
Compare numbers written in scientific notation

Examples on how to solve the GCF and LCM word problems
Example one: how to find the gcf word problem.
Step 1: First, read the problem carefully and identify the keyword(s) found in the word problem. After doing this, you see that the keywords in the problem are "largest" and "each."
Step 2: Next, how will you solve the problem? From the situation the problem describes, the keyword found in the word problem and the clue, which is "must be shared equally," calls for you to look for the GCF .
With this in mind, construct short expressions/sentences to represent the given word problem.
- Number of cans of juice bought= 100
- Number of hamburgers bought = 50
- Number of packets of potato chips = 50
- Therefore, the largest number of students that can go for the field trip for all the food to be shared equally with no leftovers = the GCF of 100 and 50.
Merge Step 3 and 4: when dealing with the GCF, step 3 and 4 are best understood when merged.
- Start by writing down a numerical expression to represent the bolded sentence in step 2 above, then find the GCF of 100 and 50 using the prime factor method.
- Firstly, find the prime factors of each number 50 = 2 × 5 × 5. 100 = 2 × 2 × 5 × 5
- Secondly, find and highlight the prime factors that the factors have in common. 50 = 2 x 5 x 5 . 100 = 2 x 5 x 2 x 5 .
- Finally, to find the GCF, multiply their common factors together. 2 × 5 × 5 = 50
So, 50 students can go for the field trip if all the food must be shared equally with no left over.
GCF of 100 and 50 = 50
- 100 cans of juice ÷ 50 = 2 cans of juice.
- 50 hamburgers ÷ 50 = 1 hamburger
- 50 packets of potato chips ÷ 50 = 1 packet of potato chips
So, each student will get 2 cans of juice, 1 hamburger, and 1 packet of potato chips.
Step 5: Finally, check your work to know if your answer makes sense. You can do this as shown below.
To check if your answer is correct,
Firstly add the number of cans of juice, hamburgers, and packets of potato chips that each student will get = 2 + 1 + 1 = 4
Secondly, add the total number of cans of juice, hamburgers, and packets of potato chips that they bought = 100 + 50 + 50 = 200
Finally, divide the total number of cans of juice, hamburgers, and packets of potato chips by the total number of cans of juice, hamburgers, and packets of potato chips that each student will get = 200 ÷ 4 = 50
So, since the final answer equals the GCF of 100 and 50, it implies that your answer is correct and makes sense.
Example two: how to find the LCM word problem
Step 1: After carefully reading the problem, you see that the keyword in the word problem is "least."
Step 2: Next, how will you solve the problem? As you can see, the problem described and the keyword found in the word problem show that we should find the LCM .
With this in mind, form short expressions/sentences to represent the given word problem.
- Packages of sandwich rolls = 12
- Packages of sausages = 6
- Packages of hamburger buns = 8
- Packages of hamburger meat patties = 6
- Therefore, the least number of people she can serve if she buys the least number of packages of each item = the LCM of 12, 8, and 6.
Merge Step 3 and 4: Fwhen dealing with LCM, step 3 and 4 are best understood when merged.
*Now, write down a numerical expression to represent the bolded sentence in step 2 above and then proceed to find the LCM of 15 and 40 using the listing multiples method.
- Firstly, list and find the multiples of 12, 8, and 6. 12 = 12, 24, 36 … 6 = 6, 12, 24, 30, 36 … 8 = 8, 16, 24, 36 …
- Secondly, find and highlight the common multiples. 12 = 12, 24 , 36 … 6 = 6, 12, 24 , 30, 36 … 8 = 8, 16, 24 , 36 …
- Thirdly, the common multiples of the numbers are 24 , 36 …
- Finally, the least common multiple of the numbers is 24 .
So, she can serve 24 people if she buys the least number of packages of each item.
To check if your answer is correct, divide the least common multiple of 12, 8, and 6 by the number of items they bought, i.e., 4 items.
Result: 24 ÷ 4 = 6
Then if you multiply the result by 4 (the number of items) and it gives you the least multiple of 12, 8, and 6, it implies that your answer is correct.
6 × 4 = 24
So, since the final answer is equal to the LCM of 12, 8, and 6, it implies that your answer is correct and makes sense .

WHAT’S THIS ALL ABOUT?
This is math-wordproblems.com a premium math quality website with original Math activities and other contents for math practice. We provide 100% free Math ressources for kids from Grade 2 to Grade 6 to improve children skills.
PRIVACY POLICY
Our team Don't Pass on to third parties any identifiable information about mathskills4kids.com users. Your email address and other information will NEVER be given or sold to a third party.
- Add And Subtract Fractions
- Addition And Subtraction Online Practice And Worksheets
- Comparing And Ordering
- Divide Fractions
- Estimating Comparing Ordering Rounding
- Fractions And Mixed Numbers
- Fractions Worksheets And Online Exercises With Answers
- Mixed Operations
- Multiplication
- Numbers Theory
- Solving And Estimation
- Subtraction
- Whole Numbers
- Second Grade
- Third Grade
- Fourth Grade
- Fifth Grade
- Sixth Grade
SUBSCRIBE TO OUR NEWSLETTER
Use of contents.
Many contents are released for free but you're not allow to share contents directly (we advice to share website links), don't use these contents in another website or for commercial issue. You're suppose to protect downloaded contents and take it for personal or classroom use. Special rule : Teachers can use our contents to teach in class.
Report a review
For more description, you can contact us here

IMAGES
COMMENTS
To solve this problem, the first thing we have to do is break down both numbers into prime factors. 24 = 2 3 x 3. 18 = 2 x 3 2. Now, to calculate the GCF, we need to choose the common factors with the smallest exponent, which in this case will be the 2 and the 3. Once we've chosen our common factors, all we have to do is multiply them by each ...
Problem. Ronald and Tim both did their laundry today. Ronald does laundry every 6 days and Tim does laundry every 9 days. How many days will it be until Ronald and Tim both do laundry on the same day again? days. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more.
Solution: Step 1 - Represent the numbers in the prime factored form. Step 2 - GCF is the product of the factors that are common to each of the given numbers. Thus, GCF (60,90) = 2 1 × 3 1 × 5 1 = 30. Therefore, GCF of 60 and 90 = 30. We can also find the greatest common factor of three numbers or more by this method.
Example 5: only common factor is 1. Calculate the greatest common factor of 35 35 and 72. 72. State the product of prime factors for each number. Show step. \begin {aligned} & 35=5 \times 7 \\\\ & 72=2 \times 2 \times 2 \times 3 \times 3 \end {aligned} 35 = 5 × 7 72 = 2 × 2 × 2 × 3 × 3. Write all the prime factors into the Venn diagram for ...
Example 3: Determine the Greatest Common Factor of [latex]42[/latex] and [latex]126[/latex].. It is easy to rush into solving a math problem because you are already familiar with the steps on how to work it out. However, it is a good practice to pause or step back and look at the problem from a broader perspective before delving into the process of solving the problem itself.
Problem. Find the greatest common factor of 42, 28, and 70 . Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
Example 1: GCF of two simple composite numbers. Find the greatest common factor of 30 30 and 42. 42. State the product of prime factors for each number. 30=2×3×5 30 = 2× 3×5 42=2×3×7 42 = 2× 3×7. 2 Write all the prime factors for each number into a Venn diagram.
For example: Multiples of 15 are: 15, 30, 45, 60, 75, etc. Factors of 15 are: 1, 3, 5, and 15 Now, how do these apply to GCF and LCM. Let's find the GCF of 15 and 9 Prime factors of 15 = 3 * 5 Prime factors of 9 = 3 * 3 The 2 numbers share one common factor. The GCF = 3. Now, let's find the LCM for 15 and 9 Multiples of 15: 15, 30, 45, 60, 75, ...
Step 1. List the factors of each number. - Identify all the positive integers that evenly divide each of the given numbers. Step 2. Find the common factors. - Determine the common factors that both numbers share. Step 3. Identify the greatest common factor. - The GCF is the largest among the common factors.
2.2 Use a Problem Solving Strategy; 2.3 Solve a Formula for a Specific Variable; ... In the next example, the greatest common factor is a binomial. ... Find the Greatest Common Factor of Two or More Expressions. In the following exercises, find the greatest common factor. 1.
Step 1: The two numbers of which we will be taking the GCF are 27 and 36. Step 2: We will use the slide method in detail to help us find the GCF: 27 36 3 9 12 3 3 4. First, we can see that 3 is a ...
The common factors of 12 and 18 are 1, 2, 3 and 6. The greatest number in these common factors is 6, hence the GCF of 12 and 18 is 6. LCM of 12 and 18 : The first four multiples of 12 are: 12, 24 ...
Problem 6 : Two numbers are in the ratio 3 : 5 and their greatest common factor is 18. Find the numbers. Solution : Because the two numbers are in the ratio 3 : 5, the numbers can be assumed as 3x and 5x. Greatest common factor (3x, 5x) = x. But, it is given that the greatest common factor of the two numbers is 18. Then, x = 18
These word problems need the use of greatest common factors (GCFs) or least common multiples (LCMs) to solve. Mixing GCF and LCM word problems encourages students to read and think about the questions, rather than simply recognizing a pattern to the solutions. Worksheet #1 Worksheet #2 Worksheet #3 Worksheet #4. Worksheet #5 Worksheet #6. Similar:
Problem 4: Find the greatest common factor of 35 and 49. Problem 5: Compute the GCD of 72 and 90. Problem 6: What is the GCF of 15 and 25? Problem 7: Find the GCF of 16, 24, and 32. Problem 8: Calculate the greatest common factor of 56 and 64. Problem 9: Determine the GCD of 120 and 150. Problem 10: Find the GCF of 9, 15, and 21. Greatest ...
Solve the following problems: a) Tim has a bag of 36 orange-flavoured sweets and Peter has a bag of 44 grape-flavoured sweets. They have to divide up the sweets into small trays with equal number of sweets; each tray containing either orange-flavoured or grape-flavoured sweets only. If there is no remainder, find the largest possible number of ...
Greatest common factor explained. The greatest common divisor (GCD) and greatest common factor (GCF) are the same thing. To find the GCD/GCF of two numbers, list their factors, identify the common factors, and choose the largest one. For example, the GCD/GCF of 12 and 8 is 4. Numbers with a GCD/GCF of 1 are called relatively prime.
GCF and Distributive Property Problem Solving. Learn how to use the GCF in problem solving. Distinguish how to use the distributive property in problem solving. Example: Madison has 56 roses and 42 daisies to use in floral centerpieces for a party. Each centerpiece will have the same number of flowers and will contain only roses or only daisies.
Firstly, find the prime factors of each number. 28 = 2 × 2 × 7. 35= 5 × 7. Secondly, find and highlight the prime factors that the factors have in common. 28 = 2 × 2 × 7. 35= 5 × 7. Finally, to find the GCF, multiply their common factors together. Here, we only have 7 as the common factor. Therefore, the GCF of 35 and 28 is 7.
The GCF is also known as the Highest Common Factor (HCF) Let us consider the example given below: For example - The GCF of 18, 21 is 3. Because the factors of the number 18 and 21 are: Factors of 18 = 2×9 =2×3×3. Factors of 21 = 3×7. Here, the number 3 is common in both the factors of numbers. Hence, the greatest common factor of 18 and ...
Greatest Common Factor - Sample Math Practice Problems The math problems below can be generated by MathScore.com, a math practice program for schools and individual families. ... Problem Correct Answer Your Answer; 1: 6, 8: Solution 8 - 6 = 2. Does 2 divide evenly into 6? Yes. Therefore 2 is the GCF. Factors of 6: 1, 2, 3, 6 Factors of 8: 1, 2 ...
100 = 2 × 2 × 5 × 5. Secondly, find and highlight the prime factors that the factors have in common. 50 = 2 x 5 x 5. 100 = 2 x 5 x 2 x 5. Finally, to find the GCF, multiply their common factors together. 2 × 5 × 5 = 50. So, 50 students can go for the field trip if all the food must be shared equally with no left over.
Prime factorization. Write down the number they have in common only once, then write down the leftover numbers. Multiply them all together. 12 3 4 2 2 18 2 9 3 3 Numbers in common are 2 and 3 Leftover numbers are 2 and 3 2 x 3 x 2 x 3 = 36 DIVIDE BY GCF METHOD Find LCM of 12 and 18 1st Find GCF - list all factors or use your favorite method ...