

About Project Euler

What is Project Euler?
Project Euler is a series of challenging mathematical/computer programming problems that will require more than just mathematical insights to solve. Although mathematics will help you arrive at elegant and efficient methods, the use of a computer and programming skills will be required to solve most problems. The motivation for starting Project Euler, and its continuation, is to provide a platform for the inquiring mind to delve into unfamiliar areas and learn new concepts in a fun and recreational context.
Who are the problems aimed at?
The intended audience include students for whom the basic curriculum is not feeding their hunger to learn, adults whose background was not primarily mathematics but had an interest in things mathematical, and professionals who want to keep their problem solving and mathematics on the cutting edge.
Currently we have 1306553 registered members who have solved at least one problem, representing 220 locations throughout the world, and collectively using 113 different programming languages to solve the problems.
Can anyone solve the problems?
The problems range in difficulty and for many the experience is inductive chain learning. That is, by solving one problem it will expose you to a new concept that allows you to undertake a previously inaccessible problem. So the determined participant will slowly but surely work his/her way through every problem.
In order to track your progress it is necessary to setup an account and have Cookies enabled.
If you already have an account, then Sign In . Otherwise, please Register – it's completely free!
However, as the problems are challenging, then you may wish to view the Problems before registering.
"Project Euler exists to encourage, challenge, and develop the skills and enjoyment of anyone with an interest in the fascinating world of mathematics."
The page has been left unattended for too long and that link/button is no longer active. Please refresh the page.
Learn by .css-1v0lc0l{color:var(--chakra-colors-blue-500);} doing
Guided interactive problem solving that’s effective and fun. Master concepts in 15 minutes a day.
Data Analysis
Computer Science
Programming & AI
Science & Engineering
Join over 10 million people learning on Brilliant
Master concepts in 15 minutes a day.
Whether you’re a complete beginner or ready to dive into machine learning and beyond, Brilliant makes it easy to level up fast with fun, bite-sized lessons.
Effective, hands-on learning
Visual, interactive lessons make concepts feel intuitive — so even complex ideas just click. Our real-time feedback and simple explanations make learning efficient.
Learn at your level
Students and professionals alike can hone dormant skills or learn new ones. Progress through lessons and challenges tailored to your level. Designed for ages 13 to 113.
Guided bite-sized lessons
We make it easy to stay on track, see your progress, and build your problem-solving skills one concept at a time.
Stay motivated
Form a real learning habit with fun content that’s always well-paced, game-like progress tracking, and friendly reminders.
© 2024 Brilliant Worldwide, Inc., Brilliant and the Brilliant Logo are trademarks of Brilliant Worldwide, Inc.
Browse Course Material
Course info.
- Prof. Dimitris Bertsimas
Departments
- Electrical Engineering and Computer Science
- Sloan School of Management
As Taught In
- Algorithms and Data Structures
- Software Design and Engineering
- Systems Engineering
- Applied Mathematics
- Discrete Mathematics
Learning Resource Types
Introduction to mathematical programming, course description.
You are leaving MIT OpenCourseWare
Hands-On Linear Programming: Optimization With Python
Table of Contents
What Is Linear Programming?
What is mixed-integer linear programming, why is linear programming important, linear programming with python, small linear programming problem, infeasible linear programming problem, unbounded linear programming problem, resource allocation problem, installing scipy and pulp, using scipy, linear programming resources, linear programming solvers.
Linear programming is a set of techniques used in mathematical programming , sometimes called mathematical optimization, to solve systems of linear equations and inequalities while maximizing or minimizing some linear function . It’s important in fields like scientific computing, economics, technical sciences, manufacturing, transportation, military, management, energy, and so on.
The Python ecosystem offers several comprehensive and powerful tools for linear programming. You can choose between simple and complex tools as well as between free and commercial ones. It all depends on your needs.
In this tutorial, you’ll learn:
- What linear programming is and why it’s important
- Which Python tools are suitable for linear programming
- How to build a linear programming model in Python
- How to solve a linear programming problem with Python
You’ll first learn about the fundamentals of linear programming. Then you’ll explore how to implement linear programming techniques in Python. Finally, you’ll look at resources and libraries to help further your linear programming journey.
Free Bonus: 5 Thoughts On Python Mastery , a free course for Python developers that shows you the roadmap and the mindset you’ll need to take your Python skills to the next level.
Linear Programming Explanation
In this section, you’ll learn the basics of linear programming and a related discipline, mixed-integer linear programming. In the next section , you’ll see some practical linear programming examples. Later, you’ll solve linear programming and mixed-integer linear programming problems with Python.
Imagine that you have a system of linear equations and inequalities. Such systems often have many possible solutions. Linear programming is a set of mathematical and computational tools that allows you to find a particular solution to this system that corresponds to the maximum or minimum of some other linear function.
Mixed-integer linear programming is an extension of linear programming. It handles problems in which at least one variable takes a discrete integer rather than a continuous value . Although mixed-integer problems look similar to continuous variable problems at first sight, they offer significant advantages in terms of flexibility and precision.
Integer variables are important for properly representing quantities naturally expressed with integers, like the number of airplanes produced or the number of customers served.
A particularly important kind of integer variable is the binary variable . It can take only the values zero or one and is useful in making yes-or-no decisions, such as whether a plant should be built or if a machine should be turned on or off. You can also use them to mimic logical constraints.
Linear programming is a fundamental optimization technique that’s been used for decades in science- and math-intensive fields. It’s precise, relatively fast, and suitable for a range of practical applications.
Mixed-integer linear programming allows you to overcome many of the limitations of linear programming. You can approximate non-linear functions with piecewise linear functions , use semi-continuous variables , model logical constraints, and more. It’s a computationally intensive tool, but the advances in computer hardware and software make it more applicable every day.
Often, when people try to formulate and solve an optimization problem, the first question is whether they can apply linear programming or mixed-integer linear programming.
Some use cases of linear programming and mixed-integer linear programming are illustrated in the following articles:
- Gurobi Optimization Case Studies
- Five Areas of Application for Linear Programming Techniques
The importance of linear programming, and especially mixed-integer linear programming, has increased over time as computers have gotten more capable, algorithms have improved, and more user-friendly software solutions have become available.
The basic method for solving linear programming problems is called the simplex method , which has several variants. Another popular approach is the interior-point method .
Mixed-integer linear programming problems are solved with more complex and computationally intensive methods like the branch-and-bound method , which uses linear programming under the hood. Some variants of this method are the branch-and-cut method , which involves the use of cutting planes , and the branch-and-price method .
There are several suitable and well-known Python tools for linear programming and mixed-integer linear programming. Some of them are open source, while others are proprietary. Whether you need a free or paid tool depends on the size and complexity of your problem as well as on the need for speed and flexibility.
It’s worth mentioning that almost all widely used linear programming and mixed-integer linear programming libraries are native to and written in Fortran or C or C++. This is because linear programming requires computationally intensive work with (often large) matrices. Such libraries are called solvers . The Python tools are just wrappers around the solvers.
Python is suitable for building wrappers around native libraries because it works well with C/C++. You’re not going to need any C/C++ (or Fortran) for this tutorial, but if you want to learn more about this cool feature, then check out the following resources:
- Building a Python C Extension Module
- CPython Internals
- Extending Python with C or C++
Basically, when you define and solve a model, you use Python functions or methods to call a low-level library that does the actual optimization job and returns the solution to your Python object.
Several free Python libraries are specialized to interact with linear or mixed-integer linear programming solvers:
- SciPy Optimization and Root Finding
In this tutorial, you’ll use SciPy and PuLP to define and solve linear programming problems.
Linear Programming Examples
In this section, you’ll see two examples of linear programming problems:
- A small problem that illustrates what linear programming is
- A practical problem related to resource allocation that illustrates linear programming concepts in a real-world scenario
You’ll use Python to solve these two problems in the next section .
Consider the following linear programming problem:
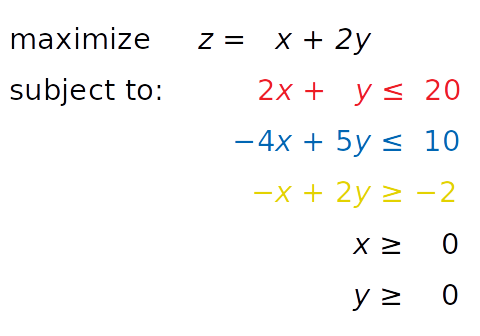
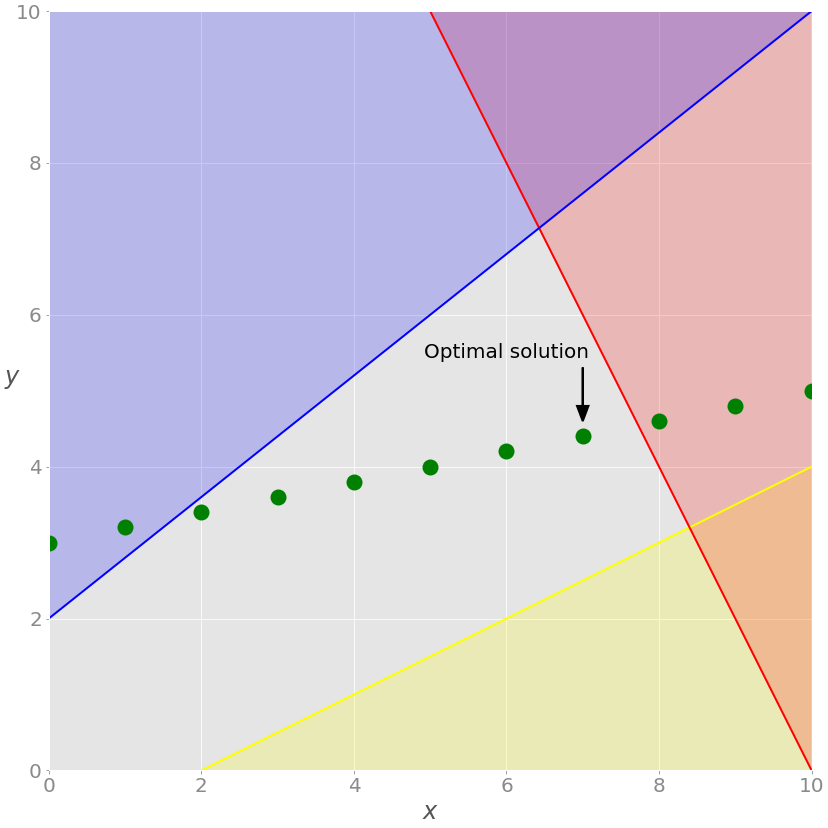
You need to find x and y such that the red, blue, and yellow inequalities, as well as the inequalities x ≥ 0 and y ≥ 0, are satisfied. At the same time, your solution must correspond to the largest possible value of z .
The independent variables you need to find—in this case x and y —are called the decision variables . The function of the decision variables to be maximized or minimized—in this case z —is called the objective function , the cost function , or just the goal . The inequalities you need to satisfy are called the inequality constraints . You can also have equations among the constraints called equality constraints .
This is how you can visualize the problem:
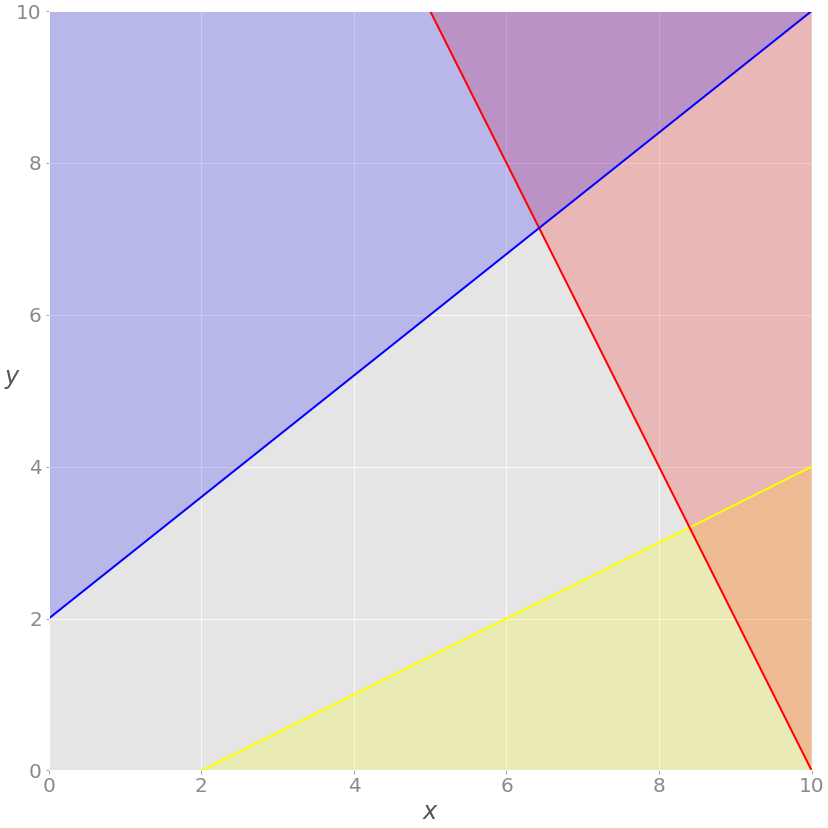
The red line represents the function 2 x + y = 20, and the red area above it shows where the red inequality is not satisfied. Similarly, the blue line is the function −4 x + 5 y = 10, and the blue area is forbidden because it violates the blue inequality. The yellow line is − x + 2 y = −2, and the yellow area below it is where the yellow inequality isn’t valid.
If you disregard the red, blue, and yellow areas, only the gray area remains. Each point of the gray area satisfies all constraints and is a potential solution to the problem. This area is called the feasible region , and its points are feasible solutions . In this case, there’s an infinite number of feasible solutions.
You want to maximize z . The feasible solution that corresponds to maximal z is the optimal solution . If you were trying to minimize the objective function instead, then the optimal solution would correspond to its feasible minimum.
Note that z is linear. You can imagine it as a plane in three-dimensional space. This is why the optimal solution must be on a vertex , or corner, of the feasible region. In this case, the optimal solution is the point where the red and blue lines intersect, as you’ll see later .
Sometimes a whole edge of the feasible region, or even the entire region, can correspond to the same value of z . In that case, you have many optimal solutions.
You’re now ready to expand the problem with the additional equality constraint shown in green:
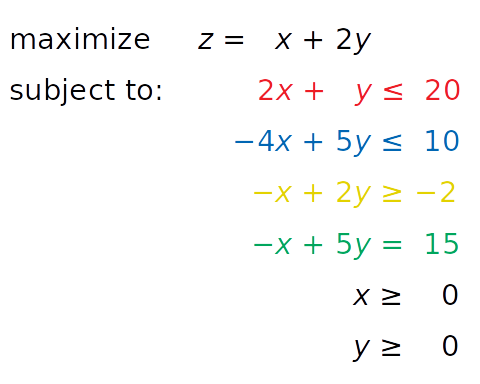
The equation − x + 5 y = 15, written in green, is new. It’s an equality constraint. You can visualize it by adding a corresponding green line to the previous image:
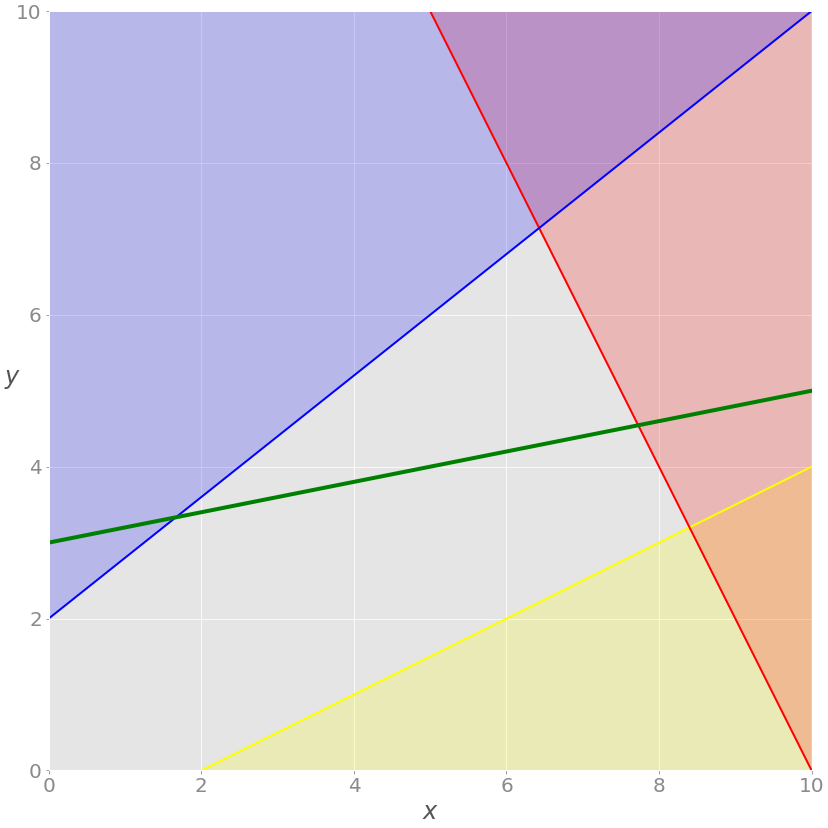
The solution now must satisfy the green equality, so the feasible region isn’t the entire gray area anymore. It’s the part of the green line passing through the gray area from the intersection point with the blue line to the intersection point with the red line. The latter point is the solution.
If you insert the demand that all values of x must be integers, then you’ll get a mixed-integer linear programming problem, and the set of feasible solutions will change once again:
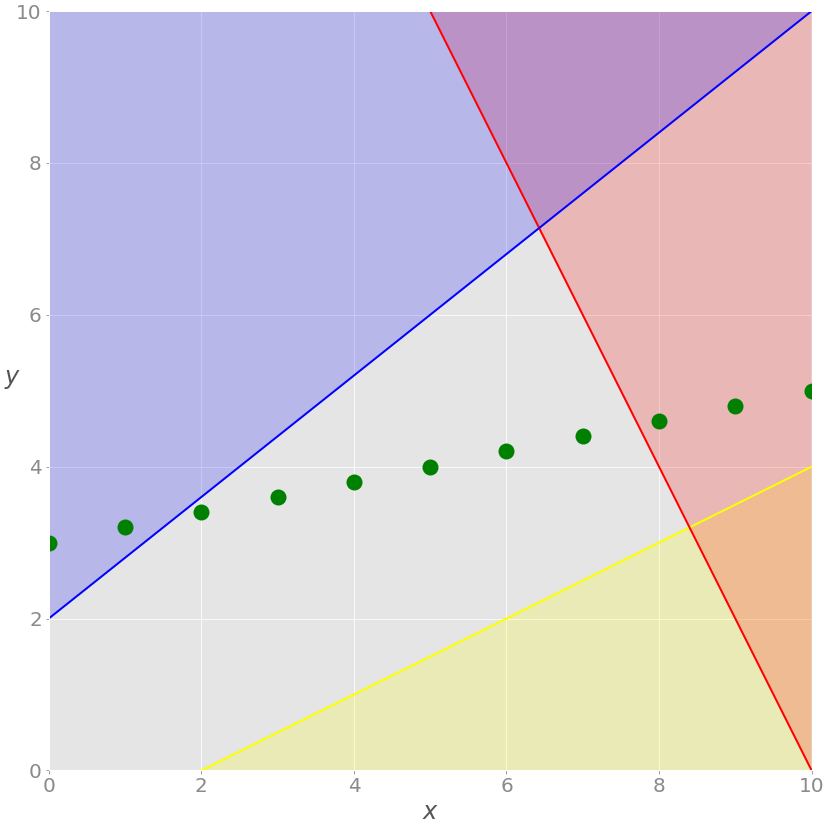
You no longer have the green line, only the points along the line where the value of x is an integer. The feasible solutions are the green points on the gray background, and the optimal one in this case is nearest to the red line.
These three examples illustrate feasible linear programming problems because they have bounded feasible regions and finite solutions.
A linear programming problem is infeasible if it doesn’t have a solution. This usually happens when no solution can satisfy all constraints at once.
For example, consider what would happen if you added the constraint x + y ≤ −1. Then at least one of the decision variables ( x or y ) would have to be negative. This is in conflict with the given constraints x ≥ 0 and y ≥ 0. Such a system doesn’t have a feasible solution, so it’s called infeasible.
Another example would be adding a second equality constraint parallel to the green line. These two lines wouldn’t have a point in common, so there wouldn’t be a solution that satisfies both constraints.
A linear programming problem is unbounded if its feasible region isn’t bounded and the solution is not finite. This means that at least one of your variables isn’t constrained and can reach to positive or negative infinity, making the objective infinite as well.
For example, say you take the initial problem above and drop the red and yellow constraints. Dropping constraints out of a problem is called relaxing the problem. In such a case, x and y wouldn’t be bounded on the positive side. You’d be able to increase them toward positive infinity, yielding an infinitely large z value.
In the previous sections, you looked at an abstract linear programming problem that wasn’t tied to any real-world application. In this subsection, you’ll find a more concrete and practical optimization problem related to resource allocation in manufacturing.
Say that a factory produces four different products, and that the daily produced amount of the first product is x ₁, the amount produced of the second product is x ₂, and so on. The goal is to determine the profit-maximizing daily production amount for each product, bearing in mind the following conditions:
The profit per unit of product is $20, $12, $40, and $25 for the first, second, third, and fourth product, respectively.
Due to manpower constraints, the total number of units produced per day can’t exceed fifty.
For each unit of the first product, three units of the raw material A are consumed. Each unit of the second product requires two units of the raw material A and one unit of the raw material B. Each unit of the third product needs one unit of A and two units of B. Finally, each unit of the fourth product requires three units of B.
Due to the transportation and storage constraints, the factory can consume up to one hundred units of the raw material A and ninety units of B per day.
The mathematical model can be defined like this:
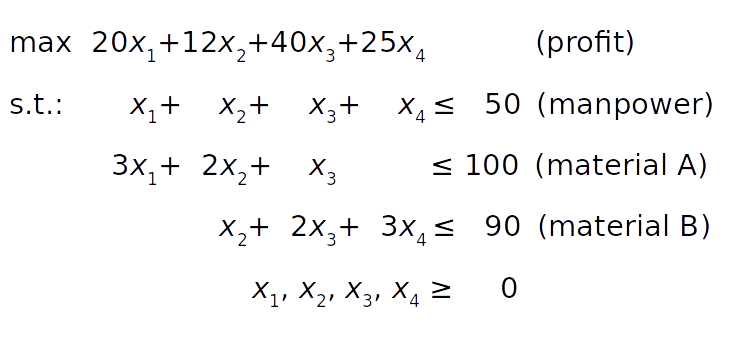
The objective function (profit) is defined in condition 1. The manpower constraint follows from condition 2. The constraints on the raw materials A and B can be derived from conditions 3 and 4 by summing the raw material requirements for each product.
Finally, the product amounts can’t be negative, so all decision variables must be greater than or equal to zero.
Unlike the previous example, you can’t conveniently visualize this one because it has four decision variables. However, the principles remain the same regardless of the dimensionality of the problem.
Linear Programming Python Implementation
In this tutorial, you’ll use two Python packages to solve the linear programming problem described above:
- SciPy is a general-purpose package for scientific computing with Python.
- PuLP is a Python linear programming API for defining problems and invoking external solvers.
SciPy is straightforward to set up. Once you install it, you’ll have everything you need to start. Its subpackage scipy.optimize can be used for both linear and nonlinear optimization .
PuLP allows you to choose solvers and formulate problems in a more natural way. The default solver used by PuLP is the COIN-OR Branch and Cut Solver (CBC) . It’s connected to the COIN-OR Linear Programming Solver (CLP) for linear relaxations and the COIN-OR Cut Generator Library (CGL) for cuts generation.
Another great open source solver is the GNU Linear Programming Kit (GLPK) . Some well-known and very powerful commercial and proprietary solutions are Gurobi , CPLEX , and XPRESS .
Besides offering flexibility when defining problems and the ability to run various solvers, PuLP is less complicated to use than alternatives like Pyomo or CVXOPT, which require more time and effort to master.
To follow this tutorial, you’ll need to install SciPy and PuLP. The examples below use version 1.4.1 of SciPy and version 2.1 of PuLP.
You can install both using pip :
You might need to run pulptest or sudo pulptest to enable the default solvers for PuLP, especially if you’re using Linux or Mac:
Optionally, you can download, install, and use GLPK. It’s free and open source and works on Windows, MacOS, and Linux. You’ll see how to use GLPK (in addition to CBC) with PuLP later in this tutorial.
On Windows, you can download the archives and run the installation files.
On MacOS, you can use Homebrew :
On Debian and Ubuntu, use apt to install glpk and glpk-utils :
On Fedora, use dnf with glpk-utils :
You might also find conda useful for installing GLPK:
After completing the installation, you can check the version of GLPK:
See GLPK’s tutorials on installing with Windows executables and Linux packages for more information.
In this section, you’ll learn how to use the SciPy optimization and root-finding library for linear programming.
To define and solve optimization problems with SciPy, you need to import scipy.optimize.linprog() :
Now that you have linprog() imported, you can start optimizing.
Let’s first solve the linear programming problem from above:
linprog() solves only minimization (not maximization) problems and doesn’t allow inequality constraints with the greater than or equal to sign (≥). To work around these issues, you need to modify your problem before starting optimization:
- Instead of maximizing z = x + 2 y, you can minimize its negative(− z = − x − 2 y).
- Instead of having the greater than or equal to sign, you can multiply the yellow inequality by −1 and get the opposite less than or equal to sign (≤).
After introducing these changes, you get a new system:
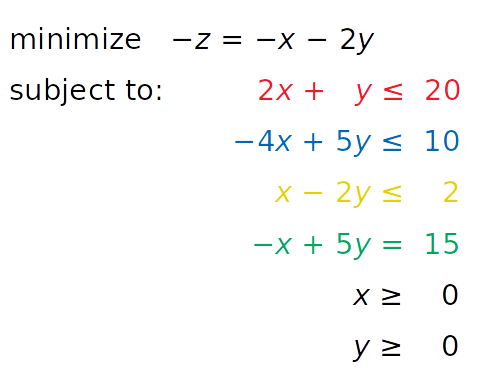
This system is equivalent to the original and will have the same solution. The only reason to apply these changes is to overcome the limitations of SciPy related to the problem formulation.
The next step is to define the input values:
You put the values from the system above into the appropriate lists, tuples , or NumPy arrays :
- obj holds the coefficients from the objective function.
- lhs_ineq holds the left-side coefficients from the inequality (red, blue, and yellow) constraints.
- rhs_ineq holds the right-side coefficients from the inequality (red, blue, and yellow) constraints.
- lhs_eq holds the left-side coefficients from the equality (green) constraint.
- rhs_eq holds the right-side coefficients from the equality (green) constraint.
Note: Please, be careful with the order of rows and columns!
The order of the rows for the left and right sides of the constraints must be the same. Each row represents one constraint.
The order of the coefficients from the objective function and left sides of the constraints must match. Each column corresponds to a single decision variable.
The next step is to define the bounds for each variable in the same order as the coefficients. In this case, they’re both between zero and positive infinity:
This statement is redundant because linprog() takes these bounds (zero to positive infinity) by default.
Note: Instead of float("inf") , you can use math.inf , numpy.inf , or scipy.inf .
Finally, it’s time to optimize and solve your problem of interest. You can do that with linprog() :
The parameter c refers to the coefficients from the objective function. A_ub and b_ub are related to the coefficients from the left and right sides of the inequality constraints, respectively. Similarly, A_eq and b_eq refer to equality constraints. You can use bounds to provide the lower and upper bounds on the decision variables.
You can use the parameter method to define the linear programming method that you want to use. There are three options:
- method="interior-point" selects the interior-point method. This option is set by default.
- method="revised simplex" selects the revised two-phase simplex method.
- method="simplex" selects the legacy two-phase simplex method.
linprog() returns a data structure with these attributes:
.con is the equality constraints residuals.
.fun is the objective function value at the optimum (if found).
.message is the status of the solution.
.nit is the number of iterations needed to finish the calculation.
.slack is the values of the slack variables, or the differences between the values of the left and right sides of the constraints.
.status is an integer between 0 and 4 that shows the status of the solution, such as 0 for when the optimal solution has been found.
.success is a Boolean that shows whether the optimal solution has been found.
.x is a NumPy array holding the optimal values of the decision variables.
You can access these values separately:
That’s how you get the results of optimization. You can also show them graphically:
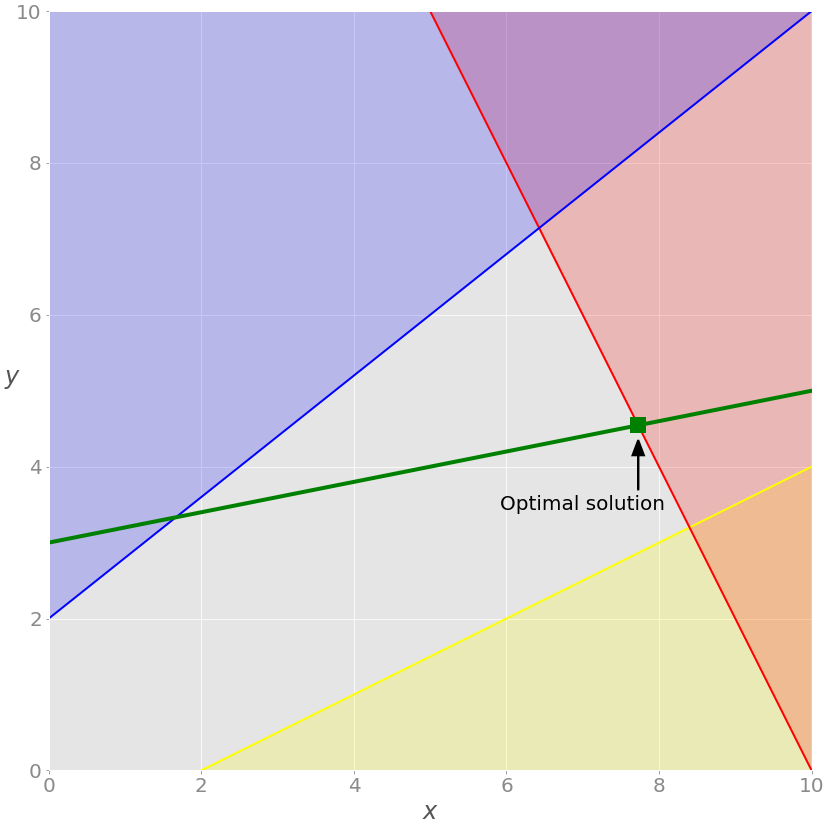
As discussed earlier, the optimal solutions to linear programming problems lie at the vertices of the feasible regions. In this case, the feasible region is just the portion of the green line between the blue and red lines. The optimal solution is the green square that represents the point of intersection between the green and red lines.
If you want to exclude the equality (green) constraint, just drop the parameters A_eq and b_eq from the linprog() call:
The solution is different from the previous case. You can see it on the chart:
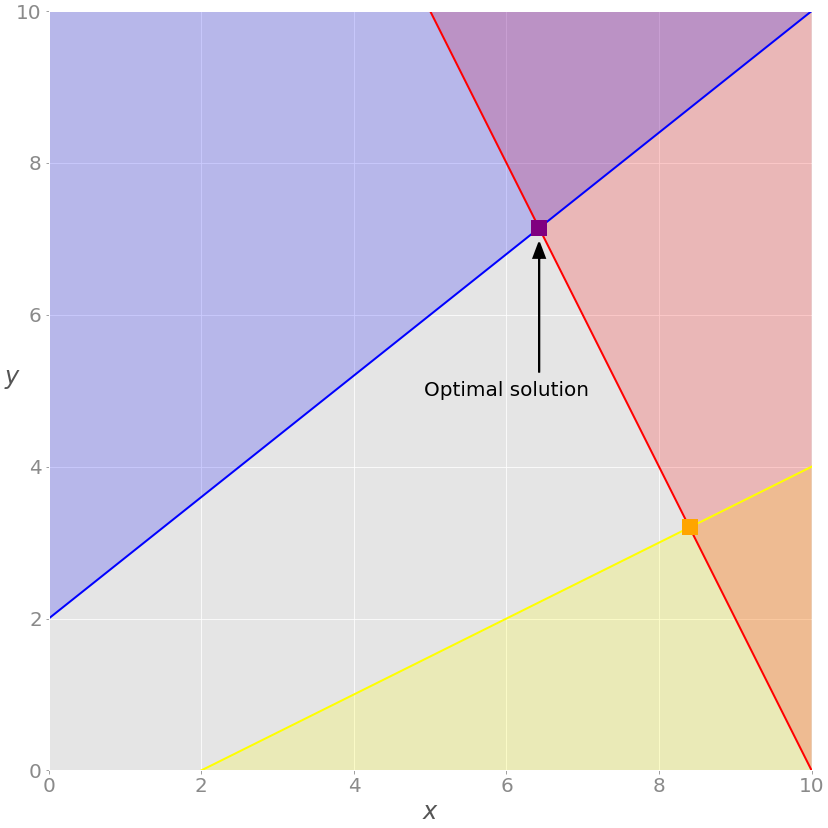
In this example, the optimal solution is the purple vertex of the feasible (gray) region where the red and blue constraints intersect. Other vertices, like the yellow one, have higher values for the objective function.
You can use SciPy to solve the resource allocation problem stated in the earlier section :
As in the previous example, you need to extract the necessary vectors and matrix from the problem above, pass them as the arguments to .linprog() , and get the results:
The result tells you that the maximal profit is 1900 and corresponds to x ₁ = 5 and x ₃ = 45. It’s not profitable to produce the second and fourth products under the given conditions. You can draw several interesting conclusions here:
The third product brings the largest profit per unit, so the factory will produce it the most.
The first slack is 0 , which means that the values of the left and right sides of the manpower (first) constraint are the same. The factory produces 50 units per day, and that’s its full capacity.
The second slack is 40 because the factory consumes 60 units of raw material A (15 units for the first product plus 45 for the third) out of a potential 100 units.
The third slack is 0 , which means that the factory consumes all 90 units of the raw material B. This entire amount is consumed for the third product. That’s why the factory can’t produce the second or fourth product at all and can’t produce more than 45 units of the third product. It lacks the raw material B.
opt.status is 0 and opt.success is True , indicating that the optimization problem was successfully solved with the optimal feasible solution.
SciPy’s linear programming capabilities are useful mainly for smaller problems. For larger and more complex problems, you might find other libraries more suitable for the following reasons:
SciPy can’t run various external solvers.
SciPy can’t work with integer decision variables.
SciPy doesn’t provide classes or functions that facilitate model building. You have to define arrays and matrices, which might be a tedious and error-prone task for large problems.
SciPy doesn’t allow you to define maximization problems directly. You must convert them to minimization problems.
SciPy doesn’t allow you to define constraints using the greater-than-or-equal-to sign directly. You must use the less-than-or-equal-to instead.
Fortunately, the Python ecosystem offers several alternative solutions for linear programming that are very useful for larger problems. One of them is PuLP, which you’ll see in action in the next section.
PuLP has a more convenient linear programming API than SciPy. You don’t have to mathematically modify your problem or use vectors and matrices. Everything is cleaner and less prone to errors.
As usual, you start by importing what you need:
Now that you have PuLP imported, you can solve your problems.
You’ll now solve this system with PuLP:
The first step is to initialize an instance of LpProblem to represent your model:
You use the sense parameter to choose whether to perform minimization ( LpMinimize or 1 , which is the default) or maximization ( LpMaximize or -1 ). This choice will affect the result of your problem.
Once that you have the model, you can define the decision variables as instances of the LpVariable class:
You need to provide a lower bound with lowBound=0 because the default value is negative infinity. The parameter upBound defines the upper bound, but you can omit it here because it defaults to positive infinity.
The optional parameter cat defines the category of a decision variable. If you’re working with continuous variables, then you can use the default value "Continuous" .
You can use the variables x and y to create other PuLP objects that represent linear expressions and constraints:
When you multiply a decision variable with a scalar or build a linear combination of multiple decision variables, you get an instance of pulp.LpAffineExpression that represents a linear expression.
Note: You can add or subtract variables or expressions, and you can multiply them with constants because PuLP classes implement some of the Python special methods that emulate numeric types like __add__() , __sub__() , and __mul__() . These methods are used to customize the behavior of operators like + , - , and * .
Similarly, you can combine linear expressions, variables, and scalars with the operators == , <= , or >= to get instances of pulp.LpConstraint that represent the linear constraints of your model.
Note: It’s also possible to build constraints with the rich comparison methods .__eq__() , .__le__() , and .__ge__() that define the behavior of the operators == , <= , and >= .
Having this in mind, the next step is to create the constraints and objective function as well as to assign them to your model. You don’t need to create lists or matrices. Just write Python expressions and use the += operator to append them to the model:
In the above code, you define tuples that hold the constraints and their names. LpProblem allows you to add constraints to a model by specifying them as tuples. The first element is a LpConstraint instance. The second element is a human-readable name for that constraint.
Setting the objective function is very similar:
Alternatively, you can use a shorter notation:
Now you have the objective function added and the model defined.
Note: You can append a constraint or objective to the model with the operator += because its class, LpProblem , implements the special method .__iadd__() , which is used to specify the behavior of += .
For larger problems, it’s often more convenient to use lpSum() with a list or other sequence than to repeat the + operator. For example, you could add the objective function to the model with this statement:
It produces the same result as the previous statement.
You can now see the full definition of this model:
The string representation of the model contains all relevant data: the variables, constraints, objective, and their names.
Note: String representations are built by defining the special method .__repr__() . For more details about .__repr__() , check out Pythonic OOP String Conversion: __repr__ vs __str__ or When Should You Use .__repr__() vs .__str__() in Python? .
Finally, you’re ready to solve the problem. You can do that by calling .solve() on your model object. If you want to use the default solver (CBC), then you don’t need to pass any arguments:
.solve() calls the underlying solver, modifies the model object, and returns the integer status of the solution, which will be 1 if the optimum is found. For the rest of the status codes, see LpStatus[] .
You can get the optimization results as the attributes of model . The function value() and the corresponding method .value() return the actual values of the attributes:
model.objective holds the value of the objective function, model.constraints contains the values of the slack variables, and the objects x and y have the optimal values of the decision variables. model.variables() returns a list with the decision variables:
As you can see, this list contains the exact objects that are created with the constructor of LpVariable .
The results are approximately the same as the ones you got with SciPy.
Note: Be careful with the method .solve() —it changes the state of the objects x and y !
You can see which solver was used by calling .solver :
The output informs you that the solver is CBC. You didn’t specify a solver, so PuLP called the default one.
If you want to run a different solver, then you can specify it as an argument of .solve() . For example, if you want to use GLPK and already have it installed, then you can use solver=GLPK(msg=False) in the last line. Keep in mind that you’ll also need to import it:
Now that you have GLPK imported, you can use it inside .solve() :
The msg parameter is used to display information from the solver. msg=False disables showing this information. If you want to include the information, then just omit msg or set msg=True .
Your model is defined and solved, so you can inspect the results the same way you did in the previous case:
You got practically the same result with GLPK as you did with SciPy and CBC.
Let’s peek and see which solver was used this time:
As you defined above with the highlighted statement model.solve(solver=GLPK(msg=False)) , the solver is GLPK.
You can also use PuLP to solve mixed-integer linear programming problems. To define an integer or binary variable, just pass cat="Integer" or cat="Binary" to LpVariable . Everything else remains the same:
In this example, you have one integer variable and get different results from before:
Now x is an integer, as specified in the model. (Technically it holds a float value with zero after the decimal point.) This fact changes the whole solution. Let’s show this on the graph:
As you can see, the optimal solution is the rightmost green point on the gray background. This is the feasible solution with the largest values of both x and y , giving it the maximal objective function value.
GLPK is capable of solving such problems as well.
Now you can use PuLP to solve the resource allocation problem from above:
The approach for defining and solving the problem is the same as in the previous example:
In this case, you use the dictionary x to store all decision variables. This approach is convenient because dictionaries can store the names or indices of decision variables as keys and the corresponding LpVariable objects as values. Lists or tuples of LpVariable instances can be useful as well.
The code above produces the following result:
As you can see, the solution is consistent with the one obtained using SciPy. The most profitable solution is to produce 5.0 units of the first product and 45.0 units of the third product per day.
Let’s make this problem more complicated and interesting. Say the factory can’t produce the first and third products in parallel due to a machinery issue. What’s the most profitable solution in this case?
Now you have another logical constraint: if x ₁ is positive, then x ₃ must be zero and vice versa. This is where binary decision variables are very useful. You’ll use two binary decision variables, y ₁ and y ₃, that’ll denote if the first or third products are generated at all:
The code is very similar to the previous example except for the highlighted lines. Here are the differences:
Line 5 defines the binary decision variables y[1] and y[3] held in the dictionary y .
Line 12 defines an arbitrarily large number M . The value 100 is large enough in this case because you can’t have more than 100 units per day.
Line 13 says that if y[1] is zero, then x[1] must be zero, else it can be any non-negative number.
Line 14 says that if y[3] is zero, then x[3] must be zero, else it can be any non-negative number.
Line 15 says that either y[1] or y[3] is zero (or both are), so either x[1] or x[3] must be zero as well.
Here’s the solution:
It turns out that the optimal approach is to exclude the first product and to produce only the third one.
Linear programming and mixed-integer linear programming are very important topics. If you want to learn more about them—and there’s much more to learn than what you saw here—then you can find plenty of resources. Here are a few to get started with:
- Wikipedia Linear Programming Article
- Wikipedia Integer Programming Article
- MIT Introduction to Mathematical Programming Course
- Brilliant.org Linear Programming Article
- CalcWorkshop What Is Linear Programming?
- BYJU’S Linear Programming Article
Gurobi Optimization is a company that offers a very fast commercial solver with a Python API. It also provides valuable resources on linear programming and mixed-integer linear programming, including the following:
- Linear Programming (LP) – A Primer on the Basics
- Mixed-Integer Programming (MIP) – A Primer on the Basics
- Choosing a Math Programming Solver
If you’re in the mood to learn optimization theory, then there’s plenty of math books out there. Here are a few popular choices:
- Linear Programming: Foundations and Extensions
- Convex Optimization
- Model Building in Mathematical Programming
- Engineering Optimization: Theory and Practice
This is just a part of what’s available. Linear programming and mixed-integer linear programming are popular and widely used techniques, so you can find countless resources to help deepen your understanding.
Just like there are many resources to help you learn linear programming and mixed-integer linear programming, there’s also a wide range of solvers that have Python wrappers available. Here’s a partial list:
- SCIP with PySCIPOpt
- Gurobi Optimizer
Some of these libraries, like Gurobi, include their own Python wrappers. Others use external wrappers. For example, you saw that you can access CBC and GLPK with PuLP.
You now know what linear programming is and how to use Python to solve linear programming problems. You also learned that Python linear programming libraries are just wrappers around native solvers. When the solver finishes its job, the wrapper returns the solution status, the decision variable values, the slack variables, the objective function, and so on.
In this tutorial, you learned how to:
- Define a model that represents your problem
- Create a Python program for optimization
- Run the optimization program to find the solution to the problem
- Retrieve the result of optimization
You used SciPy with its own solver as well as PuLP with CBC and GLPK, but you also learned that there are many other linear programming solvers and Python wrappers. You’re now ready to dive into the world of linear programming!
If you have any questions or comments, then please put them in the comments section below.
🐍 Python Tricks 💌
Get a short & sweet Python Trick delivered to your inbox every couple of days. No spam ever. Unsubscribe any time. Curated by the Real Python team.

About Mirko Stojiljković

Mirko has a Ph.D. in Mechanical Engineering and works as a university professor. He is a Pythonista who applies hybrid optimization and machine learning methods to support decision making in the energy sector.
Each tutorial at Real Python is created by a team of developers so that it meets our high quality standards. The team members who worked on this tutorial are:

Master Real-World Python Skills With Unlimited Access to Real Python
Join us and get access to thousands of tutorials, hands-on video courses, and a community of expert Pythonistas:
Join us and get access to thousands of tutorials, hands-on video courses, and a community of expert Pythonistas:
What Do You Think?
What’s your #1 takeaway or favorite thing you learned? How are you going to put your newfound skills to use? Leave a comment below and let us know.
Commenting Tips: The most useful comments are those written with the goal of learning from or helping out other students. Get tips for asking good questions and get answers to common questions in our support portal . Looking for a real-time conversation? Visit the Real Python Community Chat or join the next “Office Hours” Live Q&A Session . Happy Pythoning!
Keep Learning
Related Topics: intermediate data-science
Keep reading Real Python by creating a free account or signing in:
Already have an account? Sign-In
Almost there! Complete this form and click the button below to gain instant access:

5 Thoughts On Python Mastery
🔒 No spam. We take your privacy seriously.
5.11 Linear Programming
Learning objectives.
After completing this section, you should be able to:
- Compose an objective function to be minimized or maximized.
- Compose inequalities representing a system application.
- Apply linear programming to solve application problems.
Imagine you hear about some natural disaster striking a far-away country; it could be an earthquake, a fire, a tsunami, a tornado, a hurricane, or any other type of natural disaster. The survivors of this disaster need help—they especially need food, water, and medical supplies. You work for a company that has these supplies, and your company has decided to help by flying the needed supplies into the disaster area. They want to maximize the number of people they can help. However, there are practical constraints that need to be taken into consideration; the size of the airplanes, how much weight each airplane can carry, and so on. How do you solve this dilemma? This is where linear programming comes into play. Linear programming is a mathematical technique to solve problems involving finding maximums or minimums where a linear function is limited by various constraints.
As a field, linear programming began in the late 1930s and early 1940s. It was used by many countries during World War II; countries used linear programming to solve problems such as maximizing troop effectiveness, minimizing their own casualties, and maximizing the damage they could inflict upon the enemy. Later, businesses began to realize they could use the concept of linear programming to maximize output, minimize expenses, and so on. In short, linear programming is a method to solve problems that involve finding a maximum or minimum where a linear function is constrained by various factors.
A Mathematician Invents a “Tsunami Cannon”
On December 26, 2004, a massive earthquake occurred in the Indian Ocean. This earthquake, which scientists estimate had a magnitude of 9.0 or 9.1 on the Richter Scale, set off a wave of tsunamis across the Indian Ocean. The waves of the tsunami averaged over 30 feet (10 meters) high, and caused massive damage and loss of life across the coastal regions bordering the Indian Ocean.
Usama Kadri works as an applied mathematician at Cardiff University in Wales. His areas of research include fluid dynamics and non-linear phenomena. Lately, he has been focusing his research on the early detection and easing of the effects of tsunamis. One of his theories involves deploying a series of devices along coastlines which would fire acoustic-gravity waves (AGWs) into an oncoming tsunami, which in theory would lessen the force of the tsunami. Of course, this is all in theory, but Kadri believes it will work. There are issues with creating such a device: they would take a tremendous amount of electricity to generate an AGW, for instance, but if it would save lives, it may well be worth it.
Compose an Objective Function to Be Minimized or Maximized
An objective function is a linear function in two or more variables that describes the quantity that needs to be maximized or minimized.
Example 5.96
Composing an objective function for selling two products.
Miriam starts her own business, where she knits and sells scarves and sweaters out of high-quality wool. She can make a profit of $8 per scarf and $10 per sweater. Write an objective function that describes her profit.
Let x x represent the number of scarves sold, and let y y represent the number of sweaters sold. Let P P represent profit. Since each scarf has a profit of $8 and each sweater has a profit of $10, the objective function is P = 8 x + 10 y P = 8 x + 10 y .
Your Turn 5.96
Example 5.97, composing an objective function for production.
William’s factory produces two products, widgets and wadgets. It takes 24 minutes for his factory to make 1 widget, and 32 minutes for his factory to make 1 wadget. Write an objective function that describes the time it takes to make the products.
Let x x equal the number of widgets made; let y y equal the number of wadgets made; let T T represent total time. The objective function is T = 24 x + 32 y T = 24 x + 32 y .
Your Turn 5.97
Composing inequalities representing a system application.
For our two examples of profit and production, in an ideal world the profit a person makes and/or the number of products a company produces would have no restrictions. After all, who wouldn’t want to have an unrestricted profit? However in reality this is not the case; there are usually several variables that can restrict how much profit a person can make or how many products a company can produce. These restrictions are called constraints .
Many different variables can be constraints. When making or selling a product, the time available, the cost of manufacturing and the amount of raw materials are all constraints. In the opening scenario with the tsunami, the maximum weight on an airplane and the volume of cargo it can carry would be constraints. Constraints are expressed as linear inequalities; the list of constraints defined by the problem forms a system of linear inequalities that, along with the objective function, represent a system application.
Example 5.98
Representing the constraints for selling two products.
Two friends start their own business, where they knit and sell scarves and sweaters out of high-quality wool. They can make a profit of $8 per scarf and $10 per sweater. To make a scarf, 3 bags of knitting wool are needed; to make a sweater, 4 bags of knitting wool are needed. The friends can only make 8 items per day, and can use not more than 27 bags of knitting wool per day. Write the inequalities that represent the constraints. Then summarize what has been described thus far by writing the objective function for profit and the two constraints.
Let x x represent the number of scarves sold, and let y y represent the number of sweaters sold. There are two constraints: the number of items the business can make in a day (a maximum of 8) and the number of bags of knitting wool they can use per day (a maximum of 27). The first constraint (total number of items in a day) is written as:
Since each scarf takes 3 bags of knitting wool and each sweater takes 4 bags of knitting wool, the second constraint, total bags of knitting wool per day, is written as:
In summary, here are the equations that represent the new business:
P = 8 x + 10 y P = 8 x + 10 y ; This is the profit equation: The business makes $8 per scarf and $10 per sweater.
Your Turn 5.98
Example 5.99, representing constraints for production.
A factory produces two products, widgets and wadgets. It takes 24 minutes for the factory to make 1 widget, and 32 minutes for the factory to make 1 wadget. Research indicates that long-term demand for products from the factory will result in average sales of 12 widgets per day and 10 wadgets per day. Because of limitations on storage at the factory, no more than 20 widgets or 17 wadgets can be made each day. Write the inequalities that represent the constraints. Then summarize what has been described thus far by writing the objective function for time and the two constraints.
Let x x equal the number of widgets made; let y y equal the number of wadgets made. Based on the long-term demand, we know the factory must produce a minimum of 12 widgets and 10 wadgets per day. We also know because of storage limitations, the factory cannot produce more than 20 widgets per day or 17 wadgets per day. Writing those as inequalities, we have:
x ≥ 12 x ≥ 12
y ≥ 10 y ≥ 10
x ≤ 20 x ≤ 20
y ≤ 17 y ≤ 17
The number of widgets made per day must be between 12 and 20, and the number of wadgets made per day must be between 10 and 17. Therefore, we have:
12 ≤ x ≤ 20 12 ≤ x ≤ 20
10 ≤ y ≤ 17 10 ≤ y ≤ 17
The system is:
T = 24 x + 32 y T = 24 x + 32 y
T T is the variable for time; it takes 24 minutes to make a widget and 32 minutes to make a wadget.
Your Turn 5.99
Applying linear programming to solve application problems.
There are four steps that need to be completed when solving a problem using linear programming. They are as follows:
Step 1: Compose an objective function to be minimized or maximized.
Step 2: Compose inequalities representing the constraints of the system.
Step 3: Graph the system of inequalities representing the constraints.
Step 4: Find the value of the objective function at each corner point of the graphed region.
The first two steps you have already learned. Let’s continue to use the same examples to illustrate Steps 3 and 4.
Example 5.100
Solving a linear programming problem for two products.
Three friends start their own business, where they knit and sell scarves and sweaters out of high-quality wool. They can make a profit of $8 per scarf and $10 per sweater. To make a scarf, 3 bags of knitting wool are needed; to make a sweater, 4 bags of knitting wool are needed. The friends can only make 8 items per day, and can use not more than 27 bags of knitting wool per day. Determine the number of scarves and sweaters they should make each day to maximize their profit.
Step 1: Compose an objective function to be minimized or maximized. From Example 5.98 , the objective function is P = 8 x + 10 y P = 8 x + 10 y .
Step 2: Compose inequalities representing the constraints of the system. From Example 5.98 , the constraints are x + y ≤ 8 x + y ≤ 8 and 3 x + 4 y ≤ 27 3 x + 4 y ≤ 27 .
Step 3: Graph the system of inequalities representing the constraints. Using methods discussed in Graphing Linear Equations and Inequalities , the graphs of the constraints are shown below. Because the number of scarves ( x x ) and the number of sweaters ( y y ) both must be non-negative numbers (i.e., x ≥ 0 x ≥ 0 and y ≥ 0 y ≥ 0 ), we need to graph the system of inequalities in Quadrant I only. Figure 5.99 shows each constraint graphed on its own axes, while Figure 5.100 shows the graph of the system of inequalities (the two constraints graphed together). In Figure 5.100 , the large shaded region represents the area where the two constraints intersect. If you are unsure how to graph these regions, refer back to Graphing Linear Equations and Inequalities .
Step 4: Find the value of the objective function at each corner point of the graphed region. The “graphed region” is the area where both of the regions intersect; in Figure 5.101 , it is the large shaded area. The “corner points” refer to each vertex of the shaded area. Why the corner points? Because the maximum and minimum of every objective function will occur at one (or more) of the corner points. Figure 5.101 shows the location and coordinates of each corner point.
Three of the four points are readily found, as we used them to graph the regions; the fourth point, the intersection point of the two constraint lines, will have to be found using methods discussed in Systems of Linear Equations in Two Variables , either using substitution or elimination. As a reminder, set up the two equations of the constraint lines:
For this example, substitution will be used.
Substituting 8 - x 8 - x into the first equation for y y , we have
Now, substituting the 5 in for x x in either equation to solve for y y . Choosing the second equation, we have:
Therefore, x = 5 x = 5 , and y = 3 y = 3 .
To find the value of the objective function, P = 8 x + 10 y P = 8 x + 10 y , put the coordinates for each corner point into the equation and solve. The largest solution found when doing this will be the maximum value, and thus will be the answer to the question originally posed: determining the number of scarves and sweaters the new business should make each day to maximize their profit.
| Corner ( , ) | Objective Function |
|---|---|
The maximum value for the profit P P occurs when x = 5 x = 5 and y = 3 y = 3 . This means that to maximize their profit, the new business should make 5 scarves and 3 sweaters every day.
Your Turn 5.100
People in mathematics, leonid kantorovich.
Leonid Vitalyevich Kantorovich was born January 19, 1912, in St. Petersburg, Russia. Two major events affected young Leonid’s life: when he was five, the Russian Revolution began, making life in St. Petersburg very difficult; so much so that Leonid’s family fled to Belarus for a year. When Leonid was 10, his father died, leaving his mother to raise five children on her own.
Despite the hardships, Leonid showed incredible mathematical ability at a young age. When he was only 14, he enrolled in Leningrad State University to study mathematics. Four years later, at age 18, he graduated with what would be equivalent to a Ph.D. in mathematics.
Although his primary interests were in pure mathematics, in 1938 he began working on problems in economics. Supposedly, he was approached by a local plywood manufacturer with the following question: how to come up with a work schedule for eight lathes to maximize output, given the five different kinds of plywood they had at the factory. By July 1939, Leonid had come up with a solution, not only to the lathe scheduling problem but to other areas as well, such as an optimal crop rotation schedule for farmers, minimizing waste material in manufacturing, and finding optimal routes for transporting goods. The technique he discovered to solve these problems eventually became known as linear programming. He continued to use this technique for solving many other problems involving optimization, which resulted in the book The Best Use of Economic Resources , which was published in 1959. His continued work in linear programming would ultimately result in him winning the Nobel Prize of Economics in 1975.
Check Your Understanding
- P = 20 t − 10 c
- P = 20 c + 10 t
- P = 20 t + 10 c
- P = 20 c − 10 t
- P = 150 w + 180 b
- P = 150 b + 180 w
- P = 180 w + 150 b
- P = 150 w − 180 b
- P = 2.50 f + 6.75 c
- P = 2.50 f + 6.75 t
- P = 2.50 t + 6.75 f
- None of these
- 20 t + 10 c ≤ 70
- 15 t + 4 c ≥ 70
- 15 t + 4 c ≤ 70
- 20 t + 10 c ≤ 12
- 20 t + 10 c ≥ 12
- w + b ≤ 945
- 10 w + 15 b ≥ 945
- 10 w + 15 b ≤ 945
- 150 w + 180 w ≤ 945
- 150 w + 180 b ≤ 1,635
- 25 w + 30 b ≤ 1,635
- w + b ≤ 1,635
- 30 w + 25 b ≤ 1,635
- ( 0 , 0 ) , ( 0 , 12 ) , ( 10 , 2 ) , ( 12 , 0 )
- ( 0 , 0 ) , ( 0 , 12 ) , ( 2 , 10 ) , ( 4 2 3 , 0 )
- ( 0 , 0 ) , ( 17.5 , 0 ) , ( 2 , 10 ) , ( 12 , 0 )
Section 5.11 Exercises
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction
- Authors: Donna Kirk
- Publisher/website: OpenStax
- Book title: Contemporary Mathematics
- Publication date: Mar 22, 2023
- Location: Houston, Texas
- Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
- Section URL: https://openstax.org/books/contemporary-mathematics/pages/5-11-linear-programming
© Jul 25, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Solving mathematical problems using code: Project Euler
It is week 9 here at the Flatiron school and we are now approaching the end of our first module with Javascript. We have been so busy trying to digest all the new material that we have had barely anytime to catch a break. Everyday seems so long and packed yet there is never enough time. We have been moving at an accelerated pace, uncovering new topics when we are starting to barely grasp the material we are currently on. So to take a short breather from all this, I decided to take a step back to the very beginning stages of my coding journey and introduce you all to my friend Project Euler.
Project Euler
Project Euler is a series of challenging mathematical/computer programming problems that will require more than just mathematical insights to solve. Although mathematics will help you arrive at elegant and efficient methods, the use of a computer and programming skills will be required to solve most problems. The motivation for starting Project Euler, and its continuation, is to provide a platform for the inquiring mind to delve into unfamiliar areas and learn new concepts in a fun and recreational context.
I discovered Project Euler through a friend who recommended I try solving the problems on the site to enhance my coding skills to prep myself before attending a coding bootcamp. Project Euler is a site with many mathematical problems that are intended to be solved in an efficient way using code. The problems are labeled with the description/title, number of users that solved the problem, the difficulty level, and status of the problem (whether I solved it or not). Some of the problems also provide a PDF file that shows a mathematical approach to the problem using algorithms once the question has been solved.
Let’s take a look at one of the problems on the site:
“The prime factors of 13195 are 5, 7, 13 and 29. What is the largest prime factor of the number 600851475143 ?”
We are first given an example explaining what a prime factor is. From what we can tell, a prime factor is a number that is evenly divisible by a number and is also a prime number. Then we are given the number 600851475143 and are told to find the largest prime factor of this number.
Now let’s take this step by step and try to solve this problem using our coding knowledge.
First we need a method or function that can check whether a number is a factor of 600851475143. We also need a method or function that can check whether that number is a prime number.
Then we build out our largest_prime_factor_of(n) method to find the result.
In our new method, we are checking to see if every number between 1 and 600851475143 is a prime factor. If it is, then we select and store that number in an array and call .last on the array to return the greatest prime factor. Now I’m sure our logic works perfectly fine but when I ran this code, it went on for longer than 5 minutes so I terminated the process. Since 600851475143 is a very large number, it takes quite a bit of time for the system to calculate whether each number up to the given number is a prime factor or not.
So instead of having to calculate every single number up to 600851475143, we can simply reject all the numbers we don’t want to calculate using prime factorization. We can do this by dividing the number by it’s first prime factor until the only prime factor is itself.
Great! We can now see that our code returns the correct value in an acceptable amount of time. But we can further refactor this code to be more efficient than it is now by requiring and using the built in ruby Prime class.
- https://projecteuler.net

Written by James Rhee
Text to speech
- Docs »
- Introduction
- Edit on GitHub
Nothing in the world takes place without optimization, and there is no doubt that all aspects of the world that have a rational basis can be explained by optimization methods. Leonhard Euler, 1744 (translation found in “Optimization Stories”, edited by Martin Grötschel).
Introduction ¶
This introductory chapter is a run-up to Chapter 2 onwards. It is an overview of mathematical optimization through some simple examples, presenting also the main characteristics of the solver used in this book: SCIP ( http://scip.zib.de ).
The rest of this chapter is organized as follows. Section Mathematical Optimization introduces the basics of mathematical optimization and illustrates main ideas via a simple example. Section Linear Optimization presents a real-world production problem to discuss concepts and definitions of linear-optimization model, showing details of SCIP/Python code for solving a production problem. Section Integer Optimization introduces an integer optimization model by adding integer conditions to variables, taking as an example a simple puzzle sometimes used in junior high school examinations. A simple transportation problem, which is a special form of the linear optimization problem, along with its solution is discussed in Section Transportation Problem . Here we show how to model an optimization problem as a function, using SCIP/Python. Section Duality explains duality, an important theoretical background of linear optimization, by taking a transportation problem as an example. Section Multi-product Transportation Problem presents a multi-commodity transportation problem, which is an generalization of the transportation, and describes how to handle sparse data with SCIP/Python. Section Blending problem introduces mixture problems as an application example of linear optimization. Section Fraction optimization problem presents the fraction optimization problem, showing two ways to reduce it to a linear problem. Section Multi-Constrained Knapsack Problem illustrates a knapsack problem with details of its solution procedure, including an explanation on how to debug a formulation. Section The Modern Diet Problem considers how to cope with nutritional problems, showing an example of an optimization problem with no solution.
Mathematical Optimization ¶
Let us start by describing what mathematical optimization is: it is the science of finding the “best” solution based on a given objective function, i.e., finding a solution which is at least as good and any other possible solution. In order to do this, we must start by describing the actual problem in terms of mathematical formulas; then, we will need a methodology to obtain an optimal solution from these formulas. Usually, these formulas consist of constraints, describing conditions that must be satisfied, and by an objective function.
- objective function (which we want to maximize of minimize);
- conditions of the problem: constraint 1, constraint 2, …
- a set of variables : the unknowns that need to be found as a solution to the problem;
- a set of constraints : equations or inequalities that represent requirements in the problem as relationships between the variables
- an objective function : an expression, in terms of the defined variables, which determines e.g. the total cost, or the profit of the targeted problem.
The problem is a minimization when smaller values of the objective are preferrable, as with costs; it is a maximization when larger values are better, as with profits. The essence of the problem is the same, whether it is a minimization or a maximization (one can be converted into the other simply by putting a minus sign in the objective function).
In this text, the problem is described by the following format.
Maximize or minimize Objective function Subject to: Constraint 1 Constraint 2 …
The optimization problem seeks a solution to either minimize or maximize the objective function, while satisfying all the constraints. Such a desirable solution is called optimum or optimal solution — the best possible from all candidate solutions measured by the value of the objective function. The variables in the model are typically defined to be non-negative real numbers.
There are many kinds of mathematical optimization problems; the most basic and simple is linear optimization [1] . In a linear optimization problem, the objective function and the constraints are all linear expressions (which are straight lines, when represented graphically). If our variables are \(x_1, x_2, \ldots, x_n\) , a linear expression has the form \(a_1 x_1 + a_2 x_2 + \ldots + ax_n\) , where \(a_1, \ldots, a_n\) are constants.
For example,
is a linear optimization problem.
One of the important features of linear optimization problems is that they are easy to solve. Common texts on mathematical optimization describe in lengthy detail how a linear optimization problem can be solved. Taking the extreme case, for most practitioners, how to solve a linear optimization problem is not important. For details on how methods for solving these problems have emerged, see Margin seminar 1 . Most of the software packages for mathematical optimization support linear optimization. Given a description of the problem, an optimum solution (i.e., a solution that is guaranteed to be the best answer) to most of the practical problems can be obtained in an extremely short time.
Unfortunately, not all the problems that we find in the real world can be described as a linear optimization problem. Simple linear expressions are not enough to accurately represent many complex conditions that occur in practice. In general, optimization problems that do not fit in the linear optimization paradigm are called nonlinear optimization problems.
In practice, nonlinear optimization problems are often difficult to solve in a reliable manner. Using the mathematical optimization solver covered in this document, SCIP, it is possible to efficiently handle some nonlinear functions; in particular, quadratic optimization (involving functions which are a polynomial of up to two, such as \(x^2 + xy\) ) is well supported, especially if they are convex.
A different complication arises when some of the variables must take on integer values; in this situation, even if the expressions in the model are linear, the general case belongs to a class of difficult problems (technically, the NP-hard class [2] ). Such problems are called integer optimization problems; with ingenuity, it is possible to model a variety of practical situations under this paradigm. The case where some of the variables are restricted to integer values, and other are continuous, is called a mixed-integer optimization problem. Even for solvers that do not support nonlinear optimization, some techniques allow us to use mixed-integer optimization to approximate arbitrary nonlinear functions; these techniques (piecewise linear approximation) are described in detail in Chapter Piecewise linear approximation of nonlinear functions .
Linear Optimization ¶
We begin with a simple linear optimization problem; the goal is to explain the terminology commonly used optimization.
Let us start by explaining the meaning of \(x_1, x_2, x_3\) : these are values that we do not know, and which can change continuously; hence, they are called variables .
The first expression defines the function to be maximized, which is called the objective function .
The second and subsequent expressions restrict the value of the variables \(x1, x2, x3\) , and are commonly referred to as constraints . Expressions ensuring that the variables are non-negative \((x1, x2, x3 \geq 0)\) have the specific name of sign restrictions or non-negativity constraints . As these variables can take any non-negative real number, they are called real variables , or continuous variables .
In this problem, both the objective function and the constraint expressions consist of adding and subtracting the variables \(x_1, x_2, x_3\) multiplied by a constant. These are called linear expressions . The problem of maximizing (or minimizing) a linear objective function subject to linear constraints is called a linear optimization problem .
The set of values for variables \(x_1, x_2, x_3\) is called a solution , and if it satisfies all constraints it is called a feasible solution . Among feasible solutions, those that maximize (or minimize) the objective function are called optimal solutions . The maximum (or minimum) value of the objective function is called the optimum . In general, there are multiple solutions with an optimum objective value, but usually the aim is to find just one of them.
Finding such point can be explored in some methodical way; this is what a linear optimization solver does for finding the optimum. Without delay, we are going to see how to solve this example using the SCIP solver. SCIP has been developed at the Zuse Institute Berlin (ZIB), an interdisciplinary research institute for applied mathematics and computing. SCIP solver can be called from several programming languages; for this book we have chosen the very high-level language Python . For more information about SCIP and Python, see appendices SCIPintro and PYTHONintro , respectively.
The first thing to do is to read definitions contained in the SCIP module (a module is a different file containing programs written in Python). The SCIP module is called pyscipopt , and functionality defined there can be accessed with:
The instruction for using a module is import . In this statement we are importing the definitions of Model . We could also have used from pyscipopt import * , where the asterisk means to import all the definitions available in pyscipopt . .. ; we have imported just some of them, and we could have used other idioms, as we will see later. One of the features of Python is that, if the appropriate module is loaded, a program can do virtually anything [3] .
The next operation is to create an optimization model; this can be done with the Model class, which we have imported from the pyscipopt module.
With this instruction, we create an object named model , belonging the class Model (more precisely, model is a reference to that object). The model description is the (optional) string "Simple linear optimization" , passed as an argument.
There is a number of actions that can be done with objects of type Model , allowing us to add variables and constraints to the model before solving it. We start defining variables \(x_1, x_2, x_3\) (in the program, x1, x2, x3 ). We can generate a variable using the method addVar of the model object created above (a method is a function associated with objects of a class). For example, to generate a variable x1 we use the following statement:
With this statement, the method addVar of class Model is called, creating a variable x1 (to be precise, x1 holds a reference to the variable object). In Python, arguments are values passed to a function or method when calling it (each argument corresponds to a parameter that has been specified in the function definition). Arguments to this method are specified within parenthesis after addVar . There are several ways to specify arguments in Python, but the clearest way is to write argument name = argument value as a keyword argument .
Here, vtype = "C" indicates that this is a continuous variable, and name = "x1" indicates that its name (used, e.g., for printing) is the string "x1" . The complete signature (i.e., the set of parameters) for the addVar method is the following:
Arguments are, in order, the name, the type of variable, the lower bound, the upper bound, the coefficients in the objective function. The last parameter, pricedVar is used for column generation , a method that will be explained in Chapter Bin packing and cutting stock problems . In Python, when calling a method omitting keyword arguments (which are optional) default values (given after = ) are applied. In the case of addVar , all the parameters are optional. This means that if we add a variable with model.addVar() , SCIP will create a continuous, non-negative and unbounded variable, whose name is an empty string, with coefficient 0 in the objective ( obj=0 ). The default value for the lower bound is specified with lb=0.0 , and the upper bound ub is implicitly assigned the value infinity (in Python, the constant None usually means the absence of a value). When calling a function or method, keyword arguments without a default value cannot be omitted.
Functions and methods may also be called by writing the arguments without their name, in a predetermined order, as in:
Other variables may be generated similarly. Note that the third constraint \(x 3 \leq 30\) is the upper bound constraint of variable \(x_3\) , so we may write ub = 30 when declaring the variable.
Next, we will see how to enter a constraint. For specifying a constraint, we will need to create a linear expression , i.e., an expression in the form of \(c_1 x_1 + c_2 x2 + \ldots + c_n x_n\) , where each \(c_i\) is a constant and each \(x_i\) is a variable. We can specify a linear constraint through a relation between two linear expressions. In SCIP’s Python interface, the constraint \(2x1 + x2 + x3 \leq 60\) is entered by using method addConstr as follows:
The signature for addConstr (ignoring some parameters which are not of interest now) is:
SCIP supports more general cases, but for the time being let us concentrate on linear constraints. In this case, parameter relation is a linear constraint, including a left-hand side (lhs), a right-hand side (rhs), and the sense of the constraint. Both lhs and rhs may be constants, variables, or linear expressions; sense maybe "<=" for less than or equal to, ">=" for greater than or equal to, or "==" for equality. The name of the constraint is optional, the default being an empty string. Linear constraints may be specified in several ways; for example, the previous constraint could be written equivalently as:
Before solving the model, we must specify the objective using the setObjective method, as in:
The signature for setObjective is:
The first argument of setObjective is a linear (or more general) expression, and the second argument specifies the direction of the objective function with strings "minimize" (the default) or "maximize" . (The third parameter, clear , if "true" indicates that coefficients for all other variables should be set to zero.) We may also set the direction of optimization using model.setMinimize() or model.setMaximize() .
At this point, we can solve the problem using the method optimize of the model object:
After executing this statement — if the problem is feasible and bounded, thus allowing completion of the solution process —, we can output the optimal value of each variable. This can be done through method getVal of Model objects; e.g.:
The complete program for solving our model can be stated as follows:
| from pyscipopt import Model model = Model("Simple linear optimization") x1 = model.addVar(vtype="C", name="x1") x2 = model.addVar(vtype="C", name="x2") x3 = model.addVar(vtype="C", name="x3") model.addCons(2*x1 + x2 + x3 <= 60) model.addCons(x1 + 2*x2 + x3 <= 60) model.addCons(x3 <= 30) model.setObjective(15*x1 + 18*x2 + 30*x3, "maximize") model.optimize() if model.getStatus() == "optimal": print("Optimal value:", model.getObjVal()) print("Solution:") print(" x1 = ", model.getVal(x1)) print(" x2 = ", model.getVal(x2)) print(" x3 = ", model.getVal(x3)) else: print("Problem could not be solved to optimality") |
If we execute this Python program, the output will be:
| [solver progress output omitted] Optimal value: 1230.0 Solution: x1 = 10.0 x2 = 10.0 x3 = 30.0 |
The first lines, not shown, report progress of the SCIP solver (this can be suppressed) while lines 2 to 6 correspond to the output instructions of lines 14 to 16 of the previous program.
Margin seminar 1
Linear programming
Linear programming was proposed by George Dantzig in 1947, based on the work of three Nobel laureate economists: Wassily Leontief, Leonid Kantrovich, Tjalling Koopmans. At that time, the term used was “optimization in linear structure”, but it was renamed as “linear programming” in 1948, and this is the name commonly used afterwards. The simplex method developed by Dantzig has long been the almost unique algorithm for linear optimization problems, but it was pointed out that there are (mostly theoretical) cases where the method requires a very long time.
The question as to whether linear optimization problems can be solved efficiently in the theoretical sense (in other words, whether there is an algorithm which solves linear optimization problems in polynomial time) has been answered when the ellipsoid method was proposed by Leonid Khachiyan (Khachian), of the former Soviet Union, in 1979. Nevertheless, the algorithm of Khachiyan was only theoretical, and in practice the supremacy of the simplex method was unshaken. However, the interior point method proposed by Narendra Karmarkar in 1984 [4] has been proved to be theoretically efficient, and in practice it was found that its performance can be similar or higher than the simplex method’s. Currently available optimization solvers are usually equipped with both the simplex method (and its dual version, the dual simplex method ) and with interior point methods, and are designed so that users can choose the most appropriate of them.

Integer Optimization ¶
For many real-world optimization problems, sometimes it is necessary to obtain solutions composed of integers instead of real numbers. For instance, there are many puzzles like this: “In a farm having chicken and rabbits, there are 5 heads and 16 feet. How many chicken and rabbits are there?” Answer to this puzzle is meaningful if the solution has integer values only.
Let us consider a concrete puzzle.
Let us formalize this as an optimization problem with mathematical formulas. This process of describing a situation algebraically is called the formulation of a problem in mathematical optimization.
Then, the number of heads can be expressed as \(x + y + z\) . Cranes have two legs each, turtles have four legs each, and each octopus has eight legs. Therefore, the number of legs can be expressed as \(2x + 4y + 8z\) . So the set of \(x, y, z\) must satisfy the following “constraints”:
Since there are three variables and only two equations, there may be more than one solution. Therefore, we add a condition to minimize the sum \(y + z\) of the number of turtles and octopuses. This is the “objective function”. We obtain the complete model after adding the non-negativity constraints.
When we use a linear optimization solver, we obtain the solution \(x = 29.3333, y = 0, z = 2.66667\) . This is obviously a strange answer. Cranes, tortoises and octopuses can be divided when they are lined up as food on the shelves, but not when they are alive. To solve this model, we need to add conditions to force the variables to have integer values. These are called integrality constraints : \(x, y, z\) must be non-negative integers. Linear optimization problems with conditions requiring variables to be integers are called integer optimization problems . For the puzzle we are solving, thus, the correct model is:
Below is a simple Python/SCIP program for solving it. The main difference with respect to the programs that we have seen before concerns the declaration of variables; in this case, there is an argument to addVar for specifying that variables are integer: vtype="I" . Continuous variables (the default) can be explicitly declared with vtype="C" , and binary variables — a special case of integers, restricted to the values 0 or 1 — are declared with vtype="B" .
| from pyscipopt import Model model = Model("Simple linear optimization") x = model.addVar(vtype="I", name="x") y = model.addVar(vtype="I", name="y") z = model.addVar(vtype="I", name="x") model.addCons(x + y + z == 32,"Heads") model.addCons(2*x + 4*y + 8*z == 80,"Legs") model.setObjective(y + z, "minimize") model.optimize() if model.getStatus() == "optimal": print("Optimal value:", model.getObjVal()) print("Solution:") print(" x = ", model.getVal(x)) print(" y = ", model.getVal(y)) print(" z = ", model.getVal(z)) else: print("Problem could not be solved to optimality") |
For small integer optimization problems like this, the answer can be quickly found: \(x=28\) , \(y=2\) , and \(z=2\) , meaning that there are 28 cranes, 2 turtles and 2 octopuses. Notice that this solution is completely different of the continuous version’s; in general, we cannot guess the value of an integer solution from the continuous model. In general, integer-optimization problems are much harder to solve when compared to linear-optimization problems.
[ source code ]
Transportation Problem ¶
The next example is a classical linear optimization problem called the transportation problem . Consider the following scenario.

Transportation problem
| Customers \(i\) | |||||||
|---|---|---|---|---|---|---|---|
| Transportation cost \(c_{ij}\) | 1 | 2 | 3 | 4 | 5 | capacity \(M_j\) | |
| plant \(j\) | 1 | 4 | 5 | 6 | 8 | 10 | 500 |
| 2 | 6 | 4 | 3 | 5 | 8 | 500 | |
| 3 | 9 | 7 | 4 | 2 | 4 | 500 | |
| demand \(d_i\) | 80 | 270 | 250 | 160 | 180 | ||
Table Data for the transportation problem shows customer demand volumes, shipping costs from each factory to each customer, and production capacity at each factory. More precisely, \(d_i\) is the demand of customer \(i\) , where \(i =\) 1 to 5. Each plant \(j\) can supply its customers with goods but their production capacities are limited by \(M_j\) , where \(j =\) 1 to 3. Transportation cost for shipping goods from plant \(i\) to customer \(j\) is given in the table by \(c_{ij}\) .
Let us formulate the above problem as a linear optimization model. Suppose that the number of customers is \(n\) and the number of factories is \(m\) . Each customer is represented by \(i = 1, 2, \ldots, n\) , and each factory by \(j = 1, 2, \ldots, m\) . Also, let the set of customers be \(I = {1, 2, \ldots, n}\) and the set of factories \(J = {1, 2, \ldots, m}\) . Suppose that the demand amount of customer \(i\) is \(d_i\) , the transportation cost for shipping one unit of demand from plant \(i\) to customer \(j\) is \(c_{ij}\) , and that each plant \(j\) can supply its customers with goods, but their production capacities are limited by \(M_j\)
We use continuous variables as defined below.
Using the above symbols and variables, the transport problem can be formulated as the following linear optimization problem.
The objective function is the minimization of the sum of transportation costs. The first constraint requires that the demand is satisfied, and the second constraint ensures that factory capacities are not exceeded.
Let us solve this with Python/SCIP. First, we prepare the data needed for describing an instance [5] . In the transportation problem, it is necessary to prepare data defining demand amount \(d_i\) , transportation costs \(c_{ij}\) , capacities \(M_j\) . In the following program, we will use the same symbol used in the formulation for holding a Python’s dictionary. A dictionary is composed of a key and a value as its mapping, and is generated by arranging pais of keys and values in brackets, separated by commas: {key1:value1, key2:value2, ...} . (For details on dictionaries see appendix A.2.5 ).
The demand amount \(d_i\) is stored in a dictionary d with the customer’s number as the key and the demand amount as the value, and the capacity \(M_j\) is stored in the dictionary M with the factory number as the key and the capacity as the value.
In addition, a list I of customers’ numbers and a list J of factory numbers can be prepared as follows.
Actually, the dictionaries and lists above can be created at once by using the multidict function available in Python/SCIP, as follows.
When the dictionary is entered as an argument, the multidict function returns a pair of values; the first is the list of keys, and the second value is the dictionary sent as argument. Later, we will see that this function is very useful when we want to associate more than one value to each key. (For a more detailed usage of multidict , see appendix B.4 .)
Shipping cost \(c_{ij}\) has two subscripts. This is represented in Python by a dictionary c with a tuple of subscripts (customer and factory) as keys, and the corresponding costs as values. A tuple is a sequence, like a list; however, unlike a list, its contents can not be changed: a tuple is immutable . Tuples are created using parentheses and, due to the fact that they are immutable, can be used as keys of a dictionary (see appendix A.2.4 for details on tuples).
With this dictionary c , the transportation cost from factory \(j\) to customer \(i\) can be accessed with c[(i,j)] or c[i,j] (in a tuple, we can omit parenthesis).
As a programming habit, it is preferable not to use a one-letter variables such as d, M, c above. We have done it so that the same symbols are used in the formulation and in the program. However, in larger programs it is recommended to use meaningful variables names, such as demand, capacity, cost .
Let us write a program to solve the instance specified above.
| model = Model("transportation") x = {} for i in I: for j in J: x[i,j] = model.addVar(vtype="C", name="x(%s,%s)" % (i,j)) |
First, we define a Python variable x , which initially contains an empty dictionary (line 2). We then use dictionary x to store variable’s objects, each of them corresponding to an \(x_{ij}\) of our model (lines 3 to 5). As I is a list of customers’ indices, the for cycle of line 3 iterates over all customers \(i\) . Likewise, since J is a list of factory indices, the for cycle of line 4 iterates over the quantity transported from factory \(j\) to customer \(i\) (see appendix A.4.2 for more information about iteration). In the rightmost part of line 5 the variable is named x(i,j) ; this uses Python’s string format operation % , where %s represents substitution into a character string.
Next we add constraints. First, we add the constraint
which imposes that the demand is satisfied. Since this is a constraint for all customers \(i\) , a constraint \(\sum_{j=1}^m x_{ij} = d_i\) is added by the addCons method (line 2) at each iteration of the for cycle of line 1.
| for i in I: model.addCons(quicksum(x[i,j] for j in J if (i,j) in x) == d[i], name="Demand(%s)" % i) |
Notice that here we also give a name, Demand(i) , to constraints. Although, as for variables, the name of a constraint may be omitted, it is desirable to add an appropriate name for later reference (an example of this will be seen in Duality ). The quicksum function on the second line is an enhanced version of the sum function available in Python, used in Python/SCIP to do the computation of linear expressions more efficiently. It is possible to provide quicksum explicitly with a list, or with a list generated by iteration with a for statement, as we did here; these generator work in the same way as in list comprehensions in Python (see appendix A.4.2 ). In the above example, we calculate a linear expression by summing variables \(x_{ij}\) for element \(j \in J\) by means of quicksum(x[i,j] for j in J) . (For a more detailed explanation of quicksum , see appendix B.4 .)
Similarly, we add the factory capacity constraint
to the model as follows:
| for j in J: model.addCons(quicksum(x[i,j] for i in I if (i,j) in x) <= M[j], name="Capacity(%s)" % j) |
Again, we give a name Capacity(j) to each constraint. In the following, to simplify the description, names of constraints are often omitted; but in fact it is safer to give an appropriate name.
The objective function
is set using the setObjective method, as follows.
| model.setObjective(quicksum(c[i,j]*x[i,j] for (i,j) in x), "minimize") |
Finally, we can optimize the model and display the result.
| model.optimize() print("Optimal value:", model.getObjVal()) EPS = 1.e-6 for (i,j) in x: if model.getVal(x[i,j]) > EPS: print("sending quantity %10s from factory %3s to customer %3s" % (model.getVal(x[i,j]),j,i)) |
In this code, for (i,j) in x in line 4 is an iteration over dictionary x , holding our model’s variable. This iteration goes through all the tuples \((i,j)\) of customers and factories which are keys of the dictionary. Line 5 is a conditional statement for outputting only non-zero variables. Line 6 uses Python’s string formatting operator % , where %10s is converted into a 10-digit character string and %3s is converted into a 3-digit character string.
When the above program is executed, the following result is obtained. The results are shown in Table Optimal solution for the transportation problem and Figure Transportation problem .
| [solver progress output omitted] SCIP Status : problem is solved [optimal solution found] Solving Time (sec) : 0.00 Solving Nodes : 1 Primal Bound : +3.35000000000000e+03 (1 solutions) Dual Bound : +3.35000000000000e+03 Gap : 0.00 % Optimal value: 3350.0 sending quantity 230.0 from factory 2 to customer 3 sending quantity 20.0 from factory 3 to customer 3 sending quantity 160.0 from factory 3 to customer 4 sending quantity 270.0 from factory 2 to customer 2 sending quantity 80.0 from factory 1 to customer 1 sending quantity 180.0 from factory 3 to customer 5 |
| Customer \(i\) | 1 | 2 | 3 | 4 | 5 | ||
|---|---|---|---|---|---|---|---|
| Amount demanded | 80 | 270 | 250 | 160 | 180 | ||
| Plant \(j\) | Optimum volume transported | total | capacity | ||||
| 1 | 80 | 80 | 500 | ||||
| 2 | 270 | 230 | 500 | 500 | |||
| 3 | 20 | 160 | 180 | 360 | 500 | ||
Consider the following scenario.
In order to solve this problem smartly, the concept of dual problem is useful. Here, the dual problem is a linear optimization problem associated to the original problem (which in this context is called the primal problem). The derivation method and meaning of the dual problem are given in Margin seminar 2 ; here, we will explain how to use information from the dual of the transportation problem with Python/SCIP.
In order to investigate whether or not a factory can be expanded, let us first focus on the capacity constraint
For such an inequality constraint, a variable representing the difference between the right and the left hand sides, \(M_j - \sum_{i \in I} x_{ij}\) , is called a slack variable . Of course, one can easily calculate slack variables from the optimal solution, but in Python/SCIP we can look at the getSlack attribute for constraint objects. Also, the optimal dual variable for a constraint can be obtained with the getDualsolLinear attribute. This represents the amount of reduction on costs when increasing the capacity constraint by one unit (see Margin seminar 2 ).
In order to estimate the cost of additional orders from customers, we focus on the demand satisfaction constraint
Since this is an equality constraint, all slack variables are 0. The optimal value of the dual variable associated with this constraint represents the increase in costs as demand increases by one unit.
Margin seminar 2
Duality in linear programming provides a unifying theory that develops the relationships between a given linear program and another related linear program, stated in terms of variables with this shadow-price interpretation. The importance of duality is twofold. First, fully understanding the shadow-price interpretation of the optimal simplex multipliers can prove very useful in understanding the implications of a particular linear-programming model. Second, it is often possible to solve the related linear program with the shadow prices as the variables in place of, or in conjunction with, the original linear program, thereby taking advantage of some computational efficiencies. The importance of duality for computational procedures will become more apparent in later chapters on network-flow problems and large-scale systems.
Let us re-visit the wine production problem considered earlier to discuss some important concepts in linear-optimization models that play vital role in sensitivity analysis . Sensitivity analysis is important for finding out how optimal solution and optimal value may change when there is any change to the data used in the model. Since data may not always be considered as totally accurate, such analysis can be very helpful to the decision makers.
Let us assume that an entrepreneur is interested in the wine making company and would like to buy its resources. The entrepreneur then needs to find out how much to pay for each unit of each of the resources, the pure-grape wines of 2010 A, B and C. This can be done by solving the dual version of the model that we will discuss next.
Let \(y_1 , y_2\) and \(y_3\) be the price paid, per barrel of Alfrocheiro, Baga, and Castelão, respectively. Then, the total price that should be paid is the quantities of each of the wines in inventory times their prices, i.e., \(60y_1 + 60y_2 + 30y_3\) . Since the entrepreneur would like the purchasing cost to be minimum, this is the objective function for minimization. Now, for each of the resources, constraints in the model must ensure that prices are high enough for the company to sell to the entrepreneur. For instance, with two barrels of A and one barrel of B, the company can prepare blend \(D\) worth 15; hence, it must be offered \(2y_1 + y_2 \ge 15\) . Similarly we obtain \(y_1 + 2y_2 \ge 18\) and \(y_1 + y_2 + y_3 \ge 30\) for the blends M and S, respectively. Thus we can formulate a dual model, stated as follows (for a more sound derivation, using Lagrange multipliers, see lagrange ).
The variables used in the linear-optimization model of the production problem are called primal variables and their solution values directly solve the optimization problem. The linear-optimization model in this setting is called the primal model .
As seen above, associated with every primal model, there is a dual model. The relationships between primal and dual problems can provide significant information regarding the quality of solutions found and sensitivity of the coefficients used. Moreover, they also provide vital economic interpretations. For example, \(y_1\) , the price paid for one unit of Alfrocheiro pure-grape wine is called the shadow price of that resource, because it is the amount by which the optimal value of the primal model will change for a unit increase in its availability — or, equivalently, the price the company would be willing to pay for an additional unit of that resource.
Gurobi allows us to access the shadow prices (i.e., the optimal values of the dual variables associated with each constraint) by means of the .Pi attribute of the constraint class; e.g., in the model for the wine production company of program wblending we are printing these values in line 31.
Another concept important in duality is the reduced cost , which is associated with each decision variable. It is defined as the change in objective function value if one unit of some product that is normally not produced is forced into production; it can also be seen as the amount that the coefficient in the objective has to improve, for a variable that is zero in the optimal solution to become non-zero. Therefore, reduced cost is also appropriately called opportunity cost . Shadow prices and reduced costs allow sensitivity analysis in linear-optimization and help determine how sensitive the solutions are to small changes in the data. Such analysis can tell us how the solution will change if the objective function coefficients change or if the resource availability changes. It can also tell us how the solution may change if a new constraint is brought into the model. Gurobi allows us accessing the reduced costs through the .RC attribute of the variable class; e.g., x.RC is the reduced cost of variable x in the optimal solution.
As we will see later, primal and dual models can be effectively used not only to gain insights into the solution but also to find a bound for the linear-optimization relaxation of an integer-optimization model; linear-optimization relaxation is obtained by having the integrality constraints relaxed to non-integer solution values. Typically, an integer-optimization model is much harder to solve than its linear-optimization relaxation. Specialized algorithms have been designed around the relaxation versions of primal as well as dual optimization models for finding optimal solution more efficiently. Optimal solution of a relaxation model gives a bound for the optimal solution value of the underlying integer-optimization model, and that can be exploited in a branch-and-bound scheme for solving the integer optimization model.
Multi-product Transportation Problem ¶
In the previous transportation problem, we considered only one kind of goods produced at the production plants. In the real-world, however, that is a very restrictive scenario: A producer typically produces many different kinds of products and the customers typically demand different sets of the products available from the producers. Moreover, some producers may be specialized into producing only certain kinds of products while some others may only supply to certain customers. Therefore, a general instance of the transportation problem needs to be less restrictive and account for many such possibilities.

Multicommodity transportation
A more general version of the transportation problem is typically studied as a multi-commodity transportation model. A linear-optimization model can be built using decision variables \(x_{ijk}\) where \(i\) denotes the customer, \(j\) denotes the production plant and \(k\) denotes the product type. Customer demand is indexed by \(i\) and \(k\) to denote the customer and product type. Then the model can be stated as follows.
Note that the objective function addresses the minimum total cost for all possible cost combinations involving customers, production plants and product types. The first set of constraints ensure that all demands of the product types from the customers are met exactly while the second set of constraints ensure that capacity at each production plant is not exceeded by taking into account all product types and all customers.
A model for this in Python/Gurobi can be written as follows:
| def mctransp(I, J, K, c, d, M): model = Model("multi-commodity transportation") x = {} for i,j,k in c: x[i,j,k] = model.addVar(vtype="C", name="x[%s,%s,%s]" % (i, j, k)) model.update() for i in I: for k in K: model.addConstr(quicksum(x[i,j,k] for j in J if (i,j,k) in x) == d[i,k], "Demand[%s,%s]" % (i,k)) for j in J: model.addConstr(quicksum(x[i,j,k] for (i,j2,k) in x if j2 == j) <= M[j], "Capacity[%s]" % j) model.setObjective(quicksum(c[i,j,k]*x[i,j,k] for i,j,k in x), GRB.MINIMIZE) model.update() model.__data = x return model |
Variables are created in line 5. In lines 9 and 10 we create a list the variables that appear in each demand-satisfaction constraint, and the corresponding coefficients; these are then used for creating a linear expression, which is used as the left-hand side of a constraint in line 11. Capacity constraints are created in a similar way, in lines 13 to 15. For an example, consider now the same three production plants and five customers as before. Plant 1 produces two products, football and volleyball; it can supply football only to Customer 1 and volleyball to all five customers. Plant 2 produces football and basketball; it can supply football to Customers 2 and 3, basketball to Customers 1, 2 and 3. Plant 3 produces football, basketball and rugby ball; it can supply football and basketball to Customers 4 and 5, rugby ball to all five customers.
Let us specify the data for this problem in a Python program. First of all, we must state what products each of the plants can manufacture; on dictionary produce the key is the plant, to which we are associating a list of compatible products. We also create a dictionary M with the capacity of each plant (3000 units, in this instance).
The demand for each of the customers can be written as a double dictionary: for each customer, we associate a dictionary of products and quantities demanded.
For determining the transportation cost, we may specify the unit weight for each product and the transportation cost per unit of weight; then, we calculate \(c_{ijk}\) as their product:
We are now ready to construct a model using this data, and solving it:
If we execute this Python program, the output is the following:
| Optimize a model with 18 rows, 40 columns and 70 nonzeros Presolve removed 18 rows and 40 columns Presolve time: 0.00s Presolve: All rows and columns removed Iteration Objective Primal Inf. Dual Inf. Time 0 1.7400000e+04 0.000000e+00 0.000000e+00 0s Solved in 0 iterations and 0.00 seconds Optimal objective 1.740000000e+04 Optimal value: 17400.0 sending 100.0 units of 2 from plant 3 to customer 4 sending 210.0 units of 3 from plant 3 to customer 3 sending 40.0 units of 3 from plant 2 to customer 3 sending 40.0 units of 1 from plant 2 to customer 1 sending 10.0 units of 3 from plant 2 to customer 1 sending 100.0 units of 2 from plant 1 to customer 2 sending 100.0 units of 3 from plant 2 to customer 2 sending 70.0 units of 1 from plant 2 to customer 2 sending 60.0 units of 1 from plant 2 to customer 4 sending 30.0 units of 2 from plant 1 to customer 1 sending 180.0 units of 1 from plant 2 to customer 5 |
Readers may have noticed by now that for these two transportation problems, even though we have used linear-optimization models to solve them, the optimal solutions are integer-valued — as if we have solved integer-optimization models instead. This is because of the special structures of the constraints in the transportation problems that allow this property, commonly referred to as unimodularity . This property has enormous significance because, for many integer-optimization problems that can be modeled as transportation problems, we only need to solve their linear-optimization relaxations.
Blending problem ¶
Fraction optimization problem ¶, multi-constrained knapsack problem ¶.
Knapsack problems are specially structured optimization problems. The general notion of the knapsack problem is to fill up a knapsack of certain capacity with items from a given set such that the collection has maximum value with respect to some special attribute of the items. For instance, given a knapsack of certain volume and several items of different weights, the problem can be that of taking the heaviest collection of the items in the knapsack. Based on weights, the knapsack can then be appropriately filled by a collection that is optimal in the context of weight as the special attribute.
Suppose we have a knapsack of volume 10,000 cubic-cm that can carry up to 7 Kg weight. We have four items having weights 2, 3, 4 and 5, respectively, and volume 3000, 3500, 5100 and 7200, respectively. Associated with each of the items is its value of 16, 19, 23 and 28, respectively. We would like to fill the knapsack with items such that the total value is maximum.

Knapsack instance
An integer-optimization model of this problem can be found by defining the decision variables \(x_j=\) 1 if item \(j\) is taken, and \(x_j = 0\) otherwise, where \(j =\) 1 to 4. For constraints, we need to make sure that total weight does not exceed 7 kg and total volume does not exceed 10,000 cubic-cm. Thus, we have an integer-optimization model:
The standard version of the knapsack problem concerns the maximization of the profit subject to a constraint limiting the weight allowed in the knapsack to a constant \(W\) ; the objective is to \(\mbox{maximize } \sum_j {v_j x_j}\) subject to \(\sum_j {w_j x_j \leq W}\) , with \(x_j \in \{0,1\}\) , where \(v_j\) is the value of item \(j\) and \(w_j\) is its weight. A more general problem includes constraints in more than one dimension, say, \(m\) dimensions (as in the example above); this is called the multi-constrained knapsack problem, or \(m\) -dimensional knapsack problem. If we denote the “weight” of an object \(j\) in dimension \(i\) by \(a_{ij}\) and the capacity of the knapsack in this dimension by \(b_i\) , an integer-optimization model of this problem has the following structure:
A Python/Gurobi model for the multi-constrained knapsack problem is:
| def mkp(I, J, v, a, b): model = Model("mkp") x = {} for j in J: x[j] = model.addVar(vtype="B", name="x[%d]"%j) model.update() for i in I: model.addConstr(quicksum(a[i,j]*x[j] for j in J) <= b[i], "Dimension[%d]"%i) model.setObjective(quicksum(v[j]*x[j] for j in J), GRB.MAXIMIZE) model.update() return model |
This model can be used to solve the example above in the following way:
| J,v = multidict({1:16, 2:19, 3:23, 4:28}) a = {(1,1):2, (1,2):3, (1,3):4, (1,4):5, (2,1):3000, (2,2):3500, (2,3):5100, (2,4):7200, } I,b = multidict({1:7, 2:10000}) model = mkp(I, J, v, a, b) model.ModelSense = -1 model.optimize() print "Optimal value=", model.ObjVal EPS = 1.e-6 for v in model.getVars(): if v.X > EPS: print v.VarName,v.X |
The solution of this example is found by Gurobi: \(x_2=x_3=1, x_1=x_4=0\) . We will next briefly sketch how this solution is found.
Branch-and-bound ¶
Many optimization problems, such as knapsack problems, require the solutions to have integer values. In particular, variables in the knapsack problem require values of either 1 or 0 for making decision on whether to include an item in the knapsack or not. Simplex method cannot be used directly to solve for such solution values because it cannot be used to capture the integer requirements on the variables. We can write the constraints \(0 \le x_j \le 1\) for all \(j\) for the binary requirements on the variables, but the simplex method may give fractional values for the solution. Therefore, in general, solving integer-optimization models is much harder. However, we can use a systematic approach called branch-and-bound for solving an integer-optimization model, using the simplex method for solving linear-optimization relaxation model obtained by “relaxing” any integer requirement on the variables to non-negatives only. The process begins with the linear-optimization relaxation of the integer-optimization model and solves several related linear-optimization models by simplex method for ultimately finding an optimal solution of the integer-optimization model.
Let us use the previous knapsack example to illustrate this procedure. We can transform this integer-optimization model of the knapsack problem to its linear-optimization relaxation by replacing the binary requirements by the constraints \(0 \le x_j \le 1\) for all \(j\) . All feasible solutions of the integer-optimization model are also feasible for this linear-optimization relaxation; i.e., the polyhedron of the integer-optimization model is now contained within the polyhedron of its linear-optimization relaxation.
This linear-optimization relaxation can be solved easily by the simplex method. If the optimal solution found is feasible to the integer-optimization model also — i.e., it satisfies the binary constraints also, then we have found the optimal solution to the integer-optimization model. Otherwise, for this maximization problem, we can use the value of the optimal solution of the linear-optimization relaxation as the upper bound on the maximum value any solution of the integer-optimization model can possibly attain. Thus, optimal solution value of the linear-optimization relaxation provides an upper bound for the optimal solution value of the underlying integer-optimization model; this information can be suitably used for solving integer-optimization model via solving several related linear-optimization models.
The general notion of branch-and-bound scheme is to use bound on the optimal solution value in a tree search, as shown in Figure Branch-and-bound . Each leaf of the tree represents some linear-optimization relaxation of the original integer-optimization model. We start at the root of the search tree with the linear-optimization relaxation of the original integer-optimization model. Simplex method, gives the optimal solution \(x = (1,1,0.5,0)\) and objective function value 46.5. Since \(x_3 = 0.5\) is not integer and for the original integer-optimization model we need the variables to be either 0 or 1, we create two different subproblem children of the root by forcing \(x_3 =1\) and \(x_3 = 0\) , say \(P1\) and \(P2\) , respectively. Their optimal solutions are \(x= ( 1,1,0,0.4)\) with objective value 46.2 and \(x= (1, 0.333,1,0)\) with objective value 45.333, respectively. Now these two subproblems can be expanded again by branching on their fractional values just as before. The process will yield a binary search tree because \(x_j\) can only take values of 0 and 1.

Branch-and-bound
Consider the two children of \(P1\) , \(P3\) and \(P4\) . As found, the optimal solutions for \(P3\) and \(P4\) are \(x = (0,1,1,0)\) with objective function value 42 and \(x = (1,0,1,0.2)\) with objective function value 44.6, respectively. Since \(P3\) gives us a feasible solution for the integer-optimization model, we have an incumbent solution \(x = (0,1,1,0)\) with value 42. If no other feasible solution to the integer-optimization model from the tree search produces objective value larger than 42, then the incumbent is the optimal solution.
As can be seen from this small example, exploring the whole solution space can lead to a very large number of computations, as the number of nodes may potentially duplicate from one level to the other. Gurobi uses branch-and-bound in connection to other advanced techniques, such as the cutting plane approach, in order to achieve a very good performance on this process. As we will see later (e.g., in Chapter Graph problems ), there are some limitations to the size of the problems that can be tackled by Gurobi; however, a very large number of interesting, real-world problems can be solved successfully. In other situations, even if Gurobi cannot find the optimal solution, it will find a solution close to the optimum within reasonable time; in many applications, this is enough for practical implementation.
The Modern Diet Problem ¶
In this section we consider a mathematical model for maximizing diversity of diet intakes, subject to nutritional requirements and calorie restrictions. Let \(\mathcal{F}\) be a set of distinct foods and \(\mathcal{N}\) be a set of nutrients. Let \(d_{ij}\) be the amount of nutrient \(i\) in food \(j\) . The minimum and maximum intake of each nutrient \(i\) is given by \(a_i\) and \(b_i\) , respectively. An upper bound for the quantity of each food is given by \(M\) . Let \(x_j\) be the number of dishes to be used for each food \(j\) , and let \(y_j=1\) indicate if food \(j\) is chosen, \(y_j=0\) if not. Let the cost of the diet be \(v\) and the amount of intake of each nutrient be given by \(z_i\) . The problem is to minimize the number of distinct foods.
The first set of constraints ( Nutr in the program below) calculate the amount of each nutrient by summing over the selection of foods. Together with the last set of constraints (which is entered as bounds on \(z\) , line 8 in the program below), they ensure that nutrient levels \(z_i\) are maintained within the maximum and minimum amounts, \(a_i\) and \(b_i\) , as required. The second set of constraints ( Eat in the program below) impose that a dish variety \(y_j\) will be allowed into the objective (i.e., be non-zero) only if at least one unit of that dish \(x_j\) is selected. The third constraint ( Cost , line 16 in the program) calculates cost \(v\) of selecting a diet, while the other two constraints impose non-negativity and binary requirements on the variables \(x_j\) and \(y_j\) defined earlier.
In Python/Gurobi, this model can be specified as follows.
| def diet(F, N, a, b, c, d): model = Model("modern diet") x, y, z = {}, {}, {} for j in F: x[j] = model.addVar(lb=0, vtype="I", name="x[%s]" % j) y[j] = model.addVar(vtype="B", name="y[%s]" % j) for i in N: z[i] = model.addVar(lb=a[i], ub=b[i], name="z[%s]" % j) v = model.addVar(name="v") model.update() for i in N: model.addConstr(quicksum(d[j][i]*x[j] for j in F) == z[i], "Nutr[%s]" % i) model.addConstr(quicksum(c[j]*x[j] for j in F) == v, "Cost") for j in F: model.addConstr(y[j] <= x[j], "Eat[%s]" % j) model.setObjective(quicksum(y[j] for j in F), GRB.MAXIMIZE) model.__data = x, y, z, v return model |
We may use the data provided in http://www.ampl.com/EXAMPLES/MCDONALDS/diet2.dat for applying this model to a concrete instance:
| inf = GRB.INFINITY N, a, b = multidict({ "Cal" : [ 2000, inf ], "Carbo" : [ 350, 375 ], "Protein" : [ 55, inf ], "VitA" : [ 100, inf ], "VitC" : [ 100, inf ], "Calc" : [ 100, inf ], "Iron" : [ 100, inf ], }) F, c, d = multidict({ "QPounder":[1.84, {"Cal":510, "Carbo":34, "Protein":28, "VitA":15, "VitC": 6, "Calc":30, "Iron":20}], "McLean" :[2.19, {"Cal":370, "Carbo":35, "Protein":24, "VitA":15, "VitC": 10, "Calc":20, "Iron":20}], "Big Mac" :[1.84, {"Cal":500, "Carbo":42, "Protein":25, "VitA": 6, "VitC": 2, "Calc":25, "Iron":20}], "FFilet" :[1.44, {"Cal":370, "Carbo":38, "Protein":14, "VitA": 2, "VitC": 0, "Calc":15, "Iron":10}], "Chicken" :[2.29, {"Cal":400, "Carbo":42, "Protein":31, "VitA": 8, "VitC": 15, "Calc":15, "Iron": 8}], "Fries" :[ .77, {"Cal":220, "Carbo":26, "Protein": 3, "VitA": 0, "VitC": 15, "Calc": 0, "Iron": 2}], "McMuffin":[1.29, {"Cal":345, "Carbo":27, "Protein":15, "VitA": 4, "VitC": 0, "Calc":20, "Iron":15}], "1%LFMilk":[ .60, {"Cal":110, "Carbo":12, "Protein": 9, "VitA":10, "VitC": 4, "Calc":30, "Iron": 0}], "OrgJuice":[ .72, {"Cal": 80, "Carbo":20, "Protein": 1, "VitA": 2, "VitC":120, "Calc": 2, "Iron": 2}], }) |
In this specification of data we have used a new feature of the multidict function: for the same key (e.g., nutrients), we may specify more than one value, and assign it to several Python variables; for example, in line 3 we are specifying both the minimum and the maximum intake amount concerning calories; respectively, a and b . We are now ready to solve the diet optimization model; let us do it for several possibilities concerning the maximum calorie intake b["Cal"] :
The data is specified in lines 1 through 43. In lines 45 to 58, we solve this problem for different values of the maximum calorie intake, from infinity (i.e., no upper bound on calories) down to 2500. We encourage the reader to use Python/Gurobi to solve this problem, and check that the variety of dishes allowed decreases when the calorie intake is reduced. Interestingly, the amount spent does not vary monotonously: among those values of the calorie intake, the minimum price is for a maximum of calories of 3500 (see also Appendix dietinput ).
| As said before, until recently these were called problems, which had been abbreviated as ; complying to the new nomenclature, the abbreviation we will use is , for problems. |
| A class of problems which, even though no one proved it, are believed to be difficult to solve; i.e., solving these problems requires resources that grow exponentially with the size of the input. |
| Of course “anything” is an exaggeration. In a Python lecture found at the Massachusetts Institute of Technology home page there is a reference to an antigravity module. Please try it with antigravity. |
| Sometimes it is called a barrier method. |
| A problem with all the parameters substituted by numerical values is called ; this meaning is different of “objects generated from a class”, used in object-oriented programming, which are also called “instances” of the class. |
Do You Solve Programming Problems or Complete Exercises? (The Difference Matters.)

People tend to use the terms “problems” and “exercises” interchangeably. But there’s a difference—and it matters.
Professor Paul Zeitz makes the distinction.
Take 5 × 5. That’s easy, and that’s an exercise. So is 5,490,900 × 496. It’s a bit harder and will take you more time to solve, but you know what to do. That’s the key point.
“An exercise is a mathematical question that you immediately know how to answer,” explains Zeitz in a lecture series on problem-solving . “You may not answer it correctly, in fact you may never answer it correctly...but there’s no doubt about how to proceed.”
Not so with problems. A problem, according to Zeitz, “is a mathematical question that you do not know how to answer, at least initially.”
He defines problems and exercises through the lens of mathematical problem-solving, but they’re applicable to programming as well.
Each day we put our problem-solving skills to work as programmers: debugging code, learning a new topic, or even solving a problem. Exercises have their place, but as a programmer there’s no replacement for solving problems.
Exercise with Exercises
There are two ways you can benefit from exercises. First, they’re helpful when learning a new topic.
I’m learning JavaScript right now and using a mix of exercises and problems to do so. The exercises help me see patterns and get comfortable with concepts and syntax.
Here’s an example of an exercise from a project that asked me to write a function, which took an array of cars.
I had to sort the array of objects by the car_model key, in ascending order.
It’s not to say this exercise was a breeze—it wasn’t. It took me time and I got my fair share of error messages.
However, it qualifies as an exercise because I knew what I needed to do from the start.
I’d recently learned about arrays in JavaScript. I was familiar with sorting data from my experience with Python, though I had to research how to do this in JavaScript. The explicit directions helped, too.
But the concepts were still new. I needed practice putting them together, which is why this exercise was valuable. Repetition breeds familiarity, and the concepts began to solidify in my mind.
Maintain What You’ve Gained
Exercises also help keep learned information fresh.
As I learn JavaScript, I don’t want to forget everything I’ve learned about the first language I learned, Python. So I use Anki, a flashcard program, multiple times per day.
In this context, exercises help you keep a mountain of material straight, remind you of important concepts, and get more comfortable using a particular data structure or approach. It’s maintenance work on the body of knowledge you’ve gained so far.
I have over 1,000 cards that are filled with material I’ve seen many times before. Some cards have questions about syntax. Others ask me to write SQL queries or command-line or Git commands. Many others are filled with exercises, like “rotate a list of numbers to the right by one place value.”
It’s important to note that this exercise was once a problem for me. If you do a problem enough, it can become an exercise. At the same time, you can make an exercise a problem by adding a constraint .
Exercises are a slippery slope. On the one hand, they’re useful for learning purposes. On the other, it’s easy to get comfortable by sticking with exercises exclusively.
That’s the downside: staying in your comfort zone.
Dealing with Ambiguity
Programming is about problem-solving. And solving problems will take you outside of your comfort zone. This is a good thing.
For me, problems have two distinctive qualities. The first is ambiguity. Problem-solving is largely about how to effectively deal with ambiguity.
- An error message appears each time your program runs. Why? What’s going on? Where’s the bug? How can you fix it?
- You pull up a new problem statement. You read it and re-read it. At first glance, you’ve got no idea what’s going on, let alone what you need to do to solve it. You may even get the “deer in headlights” sensation that’s accompanied by a pit in the bottom of your stomach. (You picked a good problem!)
- You need to learn about relational databases. That’s pretty broad. How are you going to go about it? What to focus on first? What matters most? What do you really need to know right now ?
These examples all involve ambiguity. And all of them require solving problems , whether that’s finding and trouble-shooting a bug, solving an actual problem, or learning a new topic.
To make progress, you research, experiment, pull out the facts, create a plan, and apply a variety of problem-solving tactics. In short, you learn to figure it out. The more time you spend with a problem and the different perspectives you gain , the more layers it reveals and the closer you get to the “aha” moment.
Embrace the Struggle
The other difference with problems is the struggle. It’s real.
Problem-solving will test your mental stamina and patience. Progress can be slow, and the process tedious. I’ve toiled away at problems for hours, days, and even weeks.
It’s not to say that exercises won’t challenge you. They can. It’s one thing when you know that you need to use a particular method; you just need to get it to work properly. That’s a challenge, which can sometimes be downright frustrating.
But it’s something else entirely when you have no idea what to do from the start, which may happen multiple times when solving a problem. To me, problems are a struggle.
The best solution is to endure it and get yourself unstuck . In my experience, the struggle means I’m learning a lot and the breakthrough is usually around the corner.
As you push through the mental discomfort, you’ll find yourself thinking creatively and devising solutions you never thought of before. (You surprise and impress yourself—you know more than you think!) You’re becoming a stronger programmer.
You’ll even find yourself having fun. Problem-solving is challenging, to be sure, and even frustrating at times. But it’s also incredibly rewarding.
It’s like crossing the finish line of a half-marathon. No doubt the past 13.1 miles were grueling, but crossing the finish line was worth it and I’d do it again. Solving a problem feels the same way.
Which Is It: Problems or Exercises?
When you crack open your laptop, are you going to solve problems or complete exercises?
Exercises have benefits, and it’s fine to incorporate them into your programming sessions. I use exercises as a warm-up prior to a programming session. I’ll flip through an Anki flashcard deck for ten or fifteen minutes and work through some exercises. If I’m learning something new, like JavaScript, I may have an entire programming session devoted to exercises.
However, I devote time each day to solving problems —no matter what else I’m learning or building. Even on the days when I allocate a large chunk of time to exercises, I allocate plenty of time to solving problems, too.
So when you’re about to start a programming session, be aware what you’re setting out to do: exercises or problems. And no matter what, make time for solving problems.
Problem-solving is a skill that takes a lot of practice and time to develop. The only way to get better is to work at it each day. It’s that important, and for good reason.
We solve problems each day as programmers, and in a variety of ways. Making time to problem-solve is a no-brainer; our work as programmers depends on it.
I write about learning to program, and the best ways to go about it ( amymhaddad.com ).
Programmer and writer | howtolearneffectively.com | dailyskillplanner.com
If you read this far, thank the author to show them you care. Say Thanks
Learn to code for free. freeCodeCamp's open source curriculum has helped more than 40,000 people get jobs as developers. Get started

Math Programming Modeling Basics

Mathematical programming is an extremely powerful technology that enables companies to make better use of available resources. Mathematical programming technologies like linear programming (LP) and mixed-integer programming (MIP) have been applied in a variety of business areas, often resulting in tens or even hundreds of millions of dollars in cost savings. To give a quick sampling of the breadth of applications for LP and MIP techniques:
- Sports scheduling: The NFL uses MIP to compute better schedules.
- Manufacturing: SAP uses MIP to schedule the production of goods in factories in order to meet customer orders.
- Logistics: FedEx uses MIP to optimize the routing of packages through their shipping network.
- Electrical power distribution: New York ISO uses MIP to choose the most cost effective way to deliver electricity to customers.
- Finance: Betterment uses MIP to choose the optimal mix of assets which maximize after-tax returns while minimizing risk.
While the process of building a mathematical programming model will probably look like magic to a non-expert, the intent of this page is to provide a bit of insight into what goes on behind the magic, and hopefully give an indication of how you might wield some of this magic for yourself. Math programming practitioners typically have mathematical training and significant practical experience, but understanding a few simple concepts can help you get a sense of the overall process. This page provides a quick, high-level overview of mathematical programming, as well as a few useful links to additional information, including case studies and example models.
The important steps in moving from a business problem to a math programming solution
We’ll start our discussion at the point where you’ve identified a part of your business that could potentially benefit from optimization (note that we’ll use the terms “mathematical programming”, “math programming”, “mathematical optimization”, and “optimization” interchangeably here). Such opportunities are generally found wherever critical resources are being underutilized because multiple different business processes compete for resources. The goal of a mathematical programming model is to
- Capture the important decisions in your business process (e.g., “Should I build this product?”, “Should I send this truck to Boston?”, “Should I buy this stock?”, etc.),
- Capture the resources potentially consumed by these decisions (e.g., “Building this product uses these machines”, “Sending this truck consumes time and money”, etc.),
- Capture the potential conflicts between these activities (e.g., “The total budget is $X”, “Building these two products requires the same machine”, “If I send this truck to Boston, I can’t deliver anything to New York”, etc.), and then
- Suggest a plan of action that maximizes the overall efficiency of the process.
If this description seems a bit non-specific, that’s actually due to the flexibility of math programming. LP and MIP are highly mathematical technologies that don’t make any assumptions about the type of problem you are trying to solve or your goal in solving it. The person building the optimization model can specify what it means to maximize efficiency – maximizing profit, minimizing cost, minimizing delays, etc. Similarly, your resources can be anything – money, raw materials, machines, workers, etc. It’s up to the mathematical modeler to translate the often very tangible items that are part of the business process into the very mathematical objects that are used represent them in the optimization model.
If you have a sense that optimization could be the right tool for your business problem, you have a few options for scoping the opportunity. The simplest is probably to speak with an expert. Gurobi has a number of experts on staff, plus a network of consulting partners, that can help you size up an opportunity. The initial assessment typically only takes a few hours. We also have many customers with no background in optimization who have managed to teach themselves the relevant mathematical modeling concepts and have succeeded in building and deploying sophisticated optimization models.
From opportunity to application
Once you’ve identified a business process that could benefit from optimization, the next step is to create an optimization model to exploit the opportunity. There are three main steps to this process:
- Create the conceptual mathematical model that captures the important resources and constraints in the business problem.
- Translate the conceptual mathematical model into a computer program that builds that model.
- Solve the mathematical model using a math programming solver.
Let’s talk about each of these in more detail…
Creating the conceptual mathematical model
As we’ve noted, the first step in using optimization is to create a mathematical model of your business problem. An LP or MIP model consists of three primary ingredients:
- A set of decision variables, which capture the range of possible decisions you can make (e.g., “How many widgets should I produce?”, “Should I send a truck from New York to Boston?”, “Should these two teams play in week 1?”, etc.). Variables can be continuous (i.e., allowed to take any value between specified lower or upper bounds), or integral (i.e., only allowed to take integral values). A model that only contains continuous variables is a linear program (LP). Mixed-Integer Programming (MIP) models can contain a mix of integer and continuous variables. Integer variables (particulary binary variables) give you quite a bit more modeling power than continuous variables, but they also generally make the resulting model much more difficult to solve. If you are curious, you can refer to our LP Basics and our MIP basics pages for more information on why MIP models are harder than LP models.
- A set of constraints, which capture global limits on the values your decision variables can take (e.g., “These teams can’t play against each other more than once”, “A truck can only be sent to a single destination in a day”, “There are only enough parts to make 10 widgets today”, etc.). For LP and MIP, these constraints must be linear inequalities (e.g., “x + 2 y <= 3”).
- An objective function on the decision variables that captures the value you are trying to minimize or maximize (e.g., “Maximize profit”, “Minimize cost”, “Minimize late deliveries”, etc.). For LP and MIP, the objective function must be a linear expression.
The challenge here is to map the business problem, which may involve tangible entities like machines or products or people, into the form described above, which involves linear constraints on decision variables. At first glance, LP and MIP may appear to be a strange choice for solving business problems. As we noted above, LP and MIP allow you to state a set of linear constraints on decision variables (e.g., ‘2x + 3y + 5z <= 5’) and a linear objective on these same variables (e.g., ‘maximize x + y + z’). MIP also allows you to specify that certain variables must take integer values. These tools then compute values for your decision variables that maximize the objective function while respecting all stated linear constraints. That’s all that LP and MIP can do. While the merits of being able to optimize over a set of linear constraints might be clear if you are solving geometry problems, the suitability for production scheduling or electricity distribution problems probably isn’t so obvious.
For now, you’ll have to take our word for it that it is possible to map a wide variety of problems to LP/MIP form. Let’s spend a minute talking about why you would want to…
When faced with the task of solving a difficult problem, the first step is often to assemble a set of tools that might help to solve that problem. While you may not be able to find a tool that solves your exact problem, you can often find one that is effective at solving a related problem. While a custom tool may be able to exploit some special property of the specific problem you are solving, a general purpose tool has the advantage that it has probably been tuned and refined over a long period of time and a variety of users and uses.
This is particularly true for LP and MIP. If you can express your model as a set of linear constraints with a linear objective, over a set of continuous or integer decision variables, then you can reap the benefit of using a technology that has undergone a process of extensive refinement and improvement over the last 50+ years. The improvements in the technology have been quite spectacular , often transforming problems that were entirely intractable a decade ago into problems that are routinely solved today. What’s more, by building an LP or MIP model for your problem, you are then able to obtain the benefits of future improvements in the technology with no additional effort on your part.
To say that the benefits of expressing your problem as an LP or MIP are due to decades of effort focused on solving the problem doesn’t fully capture the virtues of LP and MIP, though. LP and MIP sit at a juncture between rich mathematical theory, elegant computational implementations, and richness of modeling and expressiveness that is quite rare and quite special. You could set the best and brightest minds at work for 50 years on many other problem types, and you would probably not wind up with technologies that are as powerful or as elegant as LP and MIP.
Mathematical Modeling
Hopefully we’ve convinced you that there are substantial benefits to formulating your problem as an LP or MIP model. If so, then the next step is to talk a bit about how that is done. The fundamental building block for a MIP model is the binary decision variable. It typically capture a yes/no decision, where a value of 1 means yes and a value of 0 means no. You can use a binary variable to represent any number of business decisions (“should I build this product?”, “should I buy this raw material?”, etc.). Constraints between binary variables represent competition for resources. Constraints between binary variables and continuous variables often capture the more detailed implications of these decisions.
Common Modeling Constructs
Let’s consider a few simple examples. If you can choose at most one from among a set of conflicting activities, that would be captured as a linear constraint on binary decision variables:
b 1 + b 2 + b 3 <= 1
If these are all binary variables, then at most one variable in the list can take value 1, and that one would correspond to the chosen activity. Similarly, changing the inequality to an equality:
b 1 + b 2 + b 3 = 1
…would force you to always choose one of the three possible activities.
Given a decision that is reflected in the value of a binary variable, you can use additional variables and constraints to capture the consequences of that decision. For example, if you need to transport items from one city to another, then a decision about whether to send a truck between those cities determines the maximum number of items that can be sent. By introducing a variable items[ij] to represent the number of items sent from city i to city j, then the following linear constraint would capture the relationship between the number of items sent and a decision about whether to send a truck with a capacity of 10 items:
items ij <= 10 * truck ij
If binary variable truck[ij] is 1, then you can send up to 10 items. If it is 0, then you can’t send any items.
These are just a few examples chosen from among a large set of idioms that are useful when building a mathematical model. A typical optimization model will consist of a mix of many straightforward linear constraints (e.g., the sum of these cost variables must respect the overall budget), along with a few more idiomatic constraints. Furthermore, a typical model will consist of thousands or even millions of constraints, but the overall size is typically the result of replicating the same set of constraints over multiple pieces of input data. One of the best ways to learn these idioms is to study example models. You’ll find examples from a variety of industries that you can browse and learn from here .
Modeling Patterns
If you ask an architect to design a house for you, his first thought is not going to be about how to pour concrete for the foundation. He’s going to try to identify important characteristics of the desired house (size, style, bedrooms, etc.), and then modify a house design with similar characteristics to meet your specific needs. Similarly, while understanding the low-level process of building an optimization model can be quite useful, the reality is that the mathematical modeling process is often mostly about recognizing common structure in your problem and customizing well-established models to capture the specifics of your problem.
Mathematical modeling has a number of commonly occurring model patterns that appear in many different applications. Examples include fixed-charge network flow, set partitioning, production planning, facility location, job shop scheduling, portfolio optimization, etc. It is well worth your time to familiarize yourself with common model types. Our website provides a number of example models that capture common model types. To reiterate, the model you need for your problem may not match any of these patterns exactly, but you are often better off approaching your problem by identifying a similar pattern and then thinking about how it could to customized to capture your problem, rather than trying to solve your problem from scratch.
While we’ve only mentioned LP and MIP so far, there are a number of interesting extensions that can also be solved efficiently. If your problem has a quadratic objective, involving products of decision variables rather than just linear terms, then you can solve your model as a Quadratic Program (QP) or a Mixed-Integer Quadratic Program (MIQP). If your model has quadratic constraints as well, you can solve your model as a Quadratically Constrained Program (QCP), or a Mixed-Integer Quadratically Constrained Program (MIQCP). These variants place a few restrictions on the form of the quadratic objective or constraint, but many important types of models can be cast in this form.
Another common class of models is non-linear programming (NLP) problems. While general NLP is an extremely difficult problem, such problems can often be solved using a very common and powerful approach called piecewise-linear approximation. By approximating the non-linear function using a series of linear functions, you can often transform what is typically an exceedingly difficult optimization problem into one that can be easily handled by an LP or MIP solver. Optimization solvers typically include modeling tools that make it straightforward to express a piecewise-linear function.
Implementing the model
Once you have an idea of how to build a math programming model that would solve your problem, the next step is to write a computer program that implements your model. Gurobi provides interfaces for most of the commonly used programming languages: C, C++, Java, .NET, Python, R, and MATLAB. When people ask us which language is best for math programming, our answer is that people should use the language they are most comfortable in. All of our interfaces are thin layers that sit on top of the same optimization algorithms (implemented in C). There are difference in our various language API’s, but ultimately those differences will have a smaller impact on your productivity than working in an unfamiliar language would. Another point to consider is that mathematical models rarely live in isolation. They typically consume data from some data source, and they produce results that are consumed by some downstream process. The languages and formats of these dependent processes will influence your choice of language.
Having said that, if you don’t have a reason to prefer one language over another, we recommend you use our Python API . We’ve found that this API increases modeling productivity substantially. It includes a number of higher-level modeling constructs that reduce the gap between the mathematical model itself and the implementation of that model, which makes it a lot easier to build and maintain optimization models.
The mechanics of building the optimization model are generally quite straightforward, once you have assembled the necessary input data. Our Getting Started with the Gurobi API Tutorials work through simple examples in each of our supported languages. This example touches on the basics of our API’s, including the process of creating a model, adding decision variables, adding constraints, setting the objective function, etc. We also include a number of functional examples that cover the use of more advanced features in our product.
Solving the model
A large part of the power of LP and MIP is that they provide a declarative approach to solving a problem. It is your job to state, or declare , your problem (the decision variables, constraints, and objective), and it is our job to find an optimal solution. The solver employs a number of very sophisticated algorithms for both LP and MIP problem types (and a number of parameters that optionally give you control over the behavior of these algorithms), but you generally don’t need to understand how these algorithms works to obtain a solution to your problem.
Your next step in building an optimization model will depend on how hands-on you’d like to be. As we noted above, if you are interested in further details about different aspects of math programming, you can refer to our Python basics discussion for more information on building a model, or our LP basics and MIP basics pages for more information on the underlying solution algorithms. You also browse our examples or our case studies .
If you are a commercial user who would like to discuss your problem with an expert, you can contact Gurobi directly . As Gurobi is free for qualified academic users, we provide direct support for installation and licensing questions and a monitored Gurobi Community Discussion Forum for other questions.
We also have a list of consulting firms who can help you to scope your problem and build a solution.
Of course, the best next step is to try Gurobi for yourself:
Guidance for Your Journey
30 day free trial for commercial users, always free for academics.
GUROBI NEWSLETTER
Latest news and releases
- Intro to Mathematical Optimization Modeling
- Chapter 1: Mathematical Programming
- Recommended Books, Blogs, and More
Try Gurobi for Free
Choose the evaluation license that fits you best, and start working with our Expert Team for technical guidance and support.
Evaluation License
Academic license, cloud trial.
Request free trial hours, so you can see how quickly and easily a model can be solved on the cloud.
Looking for documentation?
Jupyter Models
Case studies, privacy overview.
| Cookie | Duration | Description |
|---|---|---|
| _biz_flagsA | 1 year | A Cloudflare cookie set to record users’ settings as well as for authentication and analytics. |
| _biz_pendingA | 1 year | A Cloudflare cookie set to record users’ settings as well as for authentication and analytics. |
| _biz_sid | 30 minutes | This cookie is set by Bizible, to store the user's session id. |
| ARRAffinity | session | ARRAffinity cookie is set by Azure app service, and allows the service to choose the right instance established by a user to deliver subsequent requests made by that user. |
| ARRAffinitySameSite | session | This cookie is set by Windows Azure cloud, and is used for load balancing to make sure the visitor page requests are routed to the same server in any browsing session. |
| BIGipServersj02web-nginx-app_https | session | NGINX cookie |
| cookielawinfo-checkbox-advertisement | 1 year | Set by the GDPR Cookie Consent plugin, this cookie is used to record the user consent for the cookies in the "Advertisement" category . |
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| CookieLawInfoConsent | 1 year | Records the default button state of the corresponding category & the status of CCPA. It works only in coordination with the primary cookie. |
| elementor | never | This cookie is used by the website's WordPress theme. It allows the website owner to implement or change the website's content in real-time. |
| JSESSIONID | session | New Relic uses this cookie to store a session identifier so that New Relic can monitor session counts for an application. |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |
| Cookie | Duration | Description |
|---|---|---|
| __cf_bm | 30 minutes | This cookie, set by Cloudflare, is used to support Cloudflare Bot Management. |
| _biz_nA | 1 year | Bizible sets this cookie to remember users’ settings as well as for authentication and analytics. |
| _biz_uid | 1 year | This cookie is set by Bizible, to store user id on the current domain. |
| _hjAbsoluteSessionInProgress | 30 minutes | Hotjar sets this cookie to detect a user's first pageview session, which is a True/False flag set by the cookie. |
| _mkto_trk | 2 years | This cookie is set by Marketo. This allows a website to track visitor behavior on the sites on which the cookie is installed and to link a visitor to the recipient of an email marketing campaign, to measure campaign effectiveness. Tracking is performed anonymously until a user self-identifies by submitting a form. |
| bcookie | 1 year | LinkedIn sets this cookie from LinkedIn share buttons and ad tags to recognize browser ID. |
| bscookie | 1 year | LinkedIn sets this cookie to store performed actions on the website. |
| doc_langsBB | 1 year | Documentation system cookie |
| doc_version | 1 year | Documentation system cookie |
| lang | session | LinkedIn sets this cookie to remember a user's language setting. |
| lidc | 1 day | LinkedIn sets the lidc cookie to facilitate data center selection. |
| UserMatchHistory | 1 month | LinkedIn sets this cookie for LinkedIn Ads ID syncing. |
| whova_client_id | 10 years | Event agenda system cookie |
| Cookie | Duration | Description |
|---|---|---|
| _gat_UA-5909815-1 | 1 minute | A variation of the _gat cookie set by Google Analytics and Google Tag Manager to allow website owners to track visitor behaviour and measure site performance. The pattern element in the name contains the unique identity number of the account or website it relates to. |
| Cookie | Duration | Description |
|---|---|---|
| _an_uid | 7 days | 6Sense Cookie |
| _BUID | 1 year | This cookie, set by Bizible, is a universal user id to identify the same user across multiple clients’ domains. |
| _ga | 2 years | The _ga cookie, installed by Google Analytics, calculates visitor, session and campaign data and also keeps track of site usage for the site's analytics report. The cookie stores information anonymously and assigns a randomly generated number to recognize unique visitors. |
| _ga_* | 1 year 1 month 4 days | Google Analytics sets this cookie to store and count page views. |
| _gat_UA-* | 1 minute | Google Analytics sets this cookie for user behaviour tracking. |
| _gcl_au | 3 months | Provided by Google Tag Manager to experiment advertisement efficiency of websites using their services. |
| _gd_session | 4 hours | This cookie is used for collecting information on users visit to the website. It collects data such as total number of visits, average time spent on the website and the pages loaded. |
| _gd_visitor | 2 years | This cookie is used for collecting information on the users visit such as number of visits, average time spent on the website and the pages loaded for displaying targeted ads. |
| _gid | 1 day | Installed by Google Analytics, _gid cookie stores information on how visitors use a website, while also creating an analytics report of the website's performance. Some of the data that are collected include the number of visitors, their source, and the pages they visit anonymously. |
| _hjFirstSeen | 30 minutes | Hotjar sets this cookie to identify a new user’s first session. It stores the true/false value, indicating whether it was the first time Hotjar saw this user. |
| _hjIncludedInSessionSample_* | 2 minutes | Hotjar cookie that is set to determine if a user is included in the data sampling defined by a site's daily session limit. |
| _hjRecordingEnabled | never | Hotjar sets this cookie when a Recording starts and is read when the recording module is initialized, to see if the user is already in a recording in a particular session. |
| _hjRecordingLastActivity | never | Hotjar sets this cookie when a user recording starts and when data is sent through the WebSocket. |
| _hjSession_* | 30 minutes | Hotjar cookie that is set when a user first lands on a page with the Hotjar script. It is used to persist the Hotjar User ID, unique to that site on the browser. This ensures that behavior in subsequent visits to the same site will be attributed to the same user ID. |
| _hjSessionUser_* | 1 year | Hotjar cookie that is set when a user first lands on a page with the Hotjar script. It is used to persist the Hotjar User ID, unique to that site on the browser. This ensures that behavior in subsequent visits to the same site will be attributed to the same user ID. |
| _hjTLDTest | session | To determine the most generic cookie path that has to be used instead of the page hostname, Hotjar sets the _hjTLDTest cookie to store different URL substring alternatives until it fails. |
| 6suuid | 2 years | 6Sense Cookie |
| AnalyticsSyncHistory | 1 month | LinkedIn cookie |
| BE_CLA3 | 1 year 1 month 4 days | BrightEdge sets this cookie to enable data aggregation, analysis and report creation to assess marketing effectiveness and provide solutions for SEO, SEM and website performance. |
| CONSENT | 2 years | YouTube sets this cookie via embedded youtube-videos and registers anonymous statistical data. |
| dj | 10 years | DemandJump cookie |
| djaimid.a28e | 2 years | DemandJump cookiean |
| djaimses.a28e | 30 minutes | DemandJump cookie |
| li_gc | 5 months 27 days | LinkedIn Cookie |
| ln_or | 1 day | LinkedIn Cookie |
| vuid | 2 years | Vimeo installs this cookie to collect tracking information by setting a unique ID to embed videos to the website. |
| Cookie | Duration | Description |
|---|---|---|
| __adroll | 1 year 1 month | This cookie is set by AdRoll to identify users across visits and devices. It is used by real-time bidding for advertisers to display relevant advertisements. |
| __adroll_fpc | 1 year | AdRoll sets this cookie to target users with advertisements based on their browsing behaviour. |
| __adroll_shared | 1 year 1 month | Adroll sets this cookie to collect information on users across different websites for relevant advertising. |
| __ar_v4 | 1 year | This cookie is set under the domain DoubleClick, to place ads that point to the website in Google search results and to track conversion rates for these ads. |
| _fbp | 3 months | This cookie is set by Facebook to display advertisements when either on Facebook or on a digital platform powered by Facebook advertising, after visiting the website. |
| _te_ | session | Adroll cookie |
| fr | 3 months | Facebook sets this cookie to show relevant advertisements to users by tracking user behaviour across the web, on sites that have Facebook pixel or Facebook social plugin. |
| IDE | 1 year 24 days | Google DoubleClick IDE cookies are used to store information about how the user uses the website to present them with relevant ads and according to the user profile. |
| li_sugr | 3 months | LinkedIn sets this cookie to collect user behaviour data to optimise the website and make advertisements on the website more relevant. |
| test_cookie | 15 minutes | The test_cookie is set by doubleclick.net and is used to determine if the user's browser supports cookies. |
| VISITOR_INFO1_LIVE | 5 months 27 days | A cookie set by YouTube to measure bandwidth that determines whether the user gets the new or old player interface. |
| YSC | session | YSC cookie is set by Youtube and is used to track the views of embedded videos on Youtube pages. |
| yt-remote-connected-devices | never | YouTube sets this cookie to store the video preferences of the user using embedded YouTube video. |
| yt-remote-device-id | never | YouTube sets this cookie to store the video preferences of the user using embedded YouTube video. |
| yt.innertube::nextId | never | This cookie, set by YouTube, registers a unique ID to store data on what videos from YouTube the user has seen. |
| yt.innertube::requests | never | This cookie, set by YouTube, registers a unique ID to store data on what videos from YouTube the user has seen. |
Mathematics
Find the point easy problem solving (basic) max score: 5 success rate: 88.49%, maximum draws easy problem solving (basic) max score: 5 success rate: 95.75%, handshake easy problem solving (basic) max score: 10 success rate: 93.90%, minimum height triangle easy problem solving (basic) max score: 10 success rate: 92.22%, army game easy problem solving (basic) max score: 10 success rate: 84.87%, leonardo's prime factors easy problem solving (basic) max score: 10 success rate: 77.21%, connecting towns easy problem solving (basic) max score: 10 success rate: 87.52%, cutting paper squares easy problem solving (basic) max score: 15 success rate: 87.97%, summing the n series medium problem solving (basic) max score: 20 success rate: 75.14%, sherlock and moving tiles easy problem solving (basic) max score: 20 success rate: 76.49%, cookie support is required to access hackerrank.
Seems like cookies are disabled on this browser, please enable them to open this website
Advertisement
Examining primary students’ mathematical problem-solving in a programming context: towards computationally enhanced mathematics education
- Original Paper
- Published: 04 November 2020
- Volume 53 , pages 847–860, ( 2021 )
Cite this article

- Oi-Lam Ng ORCID: orcid.org/0000-0003-3736-7845 1 &
- Zhihao Cui 1
3118 Accesses
32 Citations
Explore all metrics
This paper reports on a design-based study within the context of a 3-day digital making (DM) summer camp attended by a group of students (aged 11–13) in grades 5 and 6. During the camp, students were presented with a set of mathematical problems to solve in a block-based programming environment, which was connected to various physical input sensors and output devices (e.g., push buttons, LED lights, number displays, etc.). Students’ code files, and screen captures of their computer work, were analyzed in terms of their developed computational problem-solving practices and any computational concepts that emerged during the problem-based DM. The results suggested that the designed tasks consistently supported the students’ modeling and algorithmic thinking, while also occasioning their testing and debugging practices; moreover, the students utilized computational abstractions in the form of variables, and employed different approaches, to formulate mathematical models in a programming context. This study contributes to the ‘big picture’ of how using computers might fundamentally change mathematics learning, with an emphasis on mathematical problem-solving. It also provides empirically grounded evidence to enhance the potential of computational thinking as a new literacy, and problem-solving as a global competence, in formal school settings.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
Price includes VAT (Russian Federation)
Instant access to the full article PDF.
Rent this article via DeepDyve
Institutional subscriptions

Similar content being viewed by others

Primary Mathematics Teachers’ Understanding of Computational Thinking
Exploring the characteristics of an optimal design of non-programming plugged learning for developing primary school students’ computational thinking in mathematics

Analyzing Students’ Computational Thinking and Programming Skills for Mathematical Problem Solving
Explore related subjects.
- Artificial Intelligence
Arzarello, F., Ferrara, F., & Robutti, O. (2012). Mathematical modeling with technology: The role of dynamic representations. Teaching Mathematics and Its Applications, 31 (1), 20–30.
Article Google Scholar
Baldwin, D., Walker, H. M., & Henderson, P. B. (2013). The roles of mathematics in computer science. ACM Inroads, 4 (4), 74–80. https://doi.org/10.1145/2537753.2537777 .
Barab, S., & Squire, K. (2004). Design-based research: Putting a stake in the ground. Journal of the Learning Sciences, 13 (1), 1–14.
Benton, L., Hoyles, C., Kalas, I., & Noss, R. (2017). Bridging primary programming and mathematics: Some findings of design research in England. Digital Experiences in Mathematics Education, 3 (2), 115–138. https://doi.org/10.1007/s40751-017-0028-x
Benton, L., Saunders, P., Kalas, I., Hoyles, C., & Noss, R. (2018). Designing for learning mathematics through programming: A case study of pupils engaging with place value. International Journal of Child-Computer Interaction, 16, 68–76.
Blum, W., & Leiß, D. (2007). How do students and teachers deal with modeling problems? In C. Haines, W. Blum, P. Galbraith, & S. Khan (Eds.), Mathematical modeling (ICTMA 12): Education, engineering and economics (pp. 222–231). Chichester: Horwood.
Google Scholar
Brennan, K., Resnick, M. (2012). New frameworks for studying and assessing the development of computational thinking . Paper Presented at the Conference of American Education Researcher Association, Vancouver.
Cai, J., Lew, H. C., Morris, A., Moyer, J. C., Ng, S. F., & Schmittau, J. (2005). The development of students’ algebraic thinking in earlier grades. ZDM Mathematics Education, 37 (1), 5–15. https://doi.org/10.1007/bf02655892 .
Carreira, S., & Jacinto, H. (2019). A model of mathematical problem solving with technology: The case of Marco solving-and-expressing two geometry problems. In P. Liljedahl & M. Santos-Trigo (Eds.), Mathematical problem solving (pp. 41–62). Cham: Springer.
Chapter Google Scholar
Cetin, I. (2015). Students’ understanding of loops and nested loops in computer programming: An APOS theory perspective. Canadian Journal of Science, Mathematics and Technology Education, 15 (2), 155–170.
Chu, S., Quek, F., Saenz, M., Bhangaonkar, S., & Okundaye, O. (2015). Enabling instrumental interaction through electronics making: Effects on children’s storytelling. In H. Schoenau-Fog, L. Bruni, S. Louchart, & S. Baceviciute (Eds.), Interactive storytelling. ICIDS 2015. Lecture notes in computer science (pp. 329–337). Cham: Springer.
Feurzeig, W., Papert, S. A., & Lawler, B. (2011). Programming-languages as a conceptual framework for teaching mathematics. Interactive Learning Environments, 19 (5), 487–501.
Gadanidis, G., Hughes, J. M., Minniti, L., & White, B. J. G. (2017). Computational thinking, grade 1 students and the binomial theorem. Digital Experiences in Mathematics Education, 3 (2), 77–96. https://doi.org/10.1007/s40751-016-0019-3
Greefrath, G., Hertleif, C., & Siller, H. S. (2018). Mathematical modeling with digital tools—A quantitative study on mathematising with dynamic geometry software. ZDM Mathematics Education, 50 (1–2), 233–244.
Greefrath, G., & Siller, H. S. (2017). Modeling and simulation with the help of digital tools. In G. A. Stillman, W. Blum, & G. Kaiser (Eds.), Mathematical modeling and applications (pp. 529–539). Cham: Springer.
Grover, S., & Pea, R. (2013). Computational thinking in K–12: A review of the state of the field. Educational Researcher, 42 (1), 38–43.
Hughes, J., Gadanidis, G., & Yiu, C. (2017). Digital making in elementary mathematics education. Digital Experiences in Mathematics Education, 3 (2), 139–153. https://doi.org/10.1007/s40751-016-0020-x
Kong, S. (2019). Components and methods of evaluating computational thinking for fostering creative problem-solvers in senior primary school education. In S. Kong & H. Abelson (Eds.), Computational thinking education . Singapore: Springer. https://doi.org/10.1007/978-981-13-6528-7 .
Liljedahl, P. (2016). Building thinking classrooms: Conditions for problem-solving. In P. Felmer, E. Pehkonen, & J. Kilpatrick (Eds.), Posing and solving mathematical problems (pp. 361–386). Cham: Springer.
Namukasa, I. K., Kotsopoulos, D., Floyd, L., Weber, J., Kafai, Y. B., Khan, S., et al. (2016). From computational thinking to computational participation: Towards achieving excellence through coding in elementary schools. In G. Gadanidis (Ed.), Math + coding symposium . London: Western University.
Ng, O., & Chan, T. (2019). Learning as making: Using 3D computer-aided design to enhance the learning of shapes and space in STEM-integrated ways. British Journal of Educational Technology, 50 (1), 294–308. https://doi.org/10.1111/bjet.12643
Ng, O., & Ferrara, F. (2019). Towards a materialist vision of ‘learning as making’: The case of 3D printing pens in school mathematics. International Journal of Science and Mathematics Education . https://doi.org/10.1007/s10763-019-10000-9
Niemelä, P., Partanen, T., Harsu, M., Leppänen, L., & Ihantola, P. (2017). Computational thinking as an emergent learning trajectory of mathematics. Proceedings of the 17th Koli Calling Conference on Computing Education Research—Koli Calling 17 . https://doi.org/10.1145/3141880.3141885
Organisation for Economic Co-operation and Development (OECD). (2004). The PISA 2003 assessment framework: Mathematics, reading, science and problem solving knowledge and skills . Paris: OECD Publishing. https://doi.org/10.1787/9789264101739-en
Book Google Scholar
Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas . New York: Basic Books.
Papert, S., & Harel, I. (1991). Situating constructionism. Constructionism, 36 (2), 1–11.
Pólya, G. (1945). How to solve it . Princeton: Princeton University Press.
Pei, C. Y., Weintrop, D., & Wilensky, U. (2018). Cultivating computational thinking practices and mathematical habits of mind in lattice land. Mathematical Thinking and Learning, 20 (1), 75–89. https://doi.org/10.1080/10986065.2018.1403543
Resnick, M., Maloney, J., Monroy-Hernández, A., Rusk, N., Eastmond, E., Brennan, K., & Kafai, Y. B. (2009). Scratch: Programming for all. Communications of the ACM, 52 (11), 60–67.
Rodríguez-Martínez, J., González-Calero, J., & Sáez-López, J. (2019). Computational thinking and mathematics using scratch: An experiment with sixth-grade students. Interactive Learning Environments, 28 (3), 316–327.
Roschelle, J., Pea, R., Hoadley, C., Gordin, D., & Means, B. (2000). Future of children. Children and Computer Technology, 10 (2), 76–101.
Roschelle, J., Noss, R., Blikstein, P., & Jackiw, N. (2017). Technology for learning mathematics. In J. Cai (Ed.), Compendium for research in mathematics education (pp. 853–876). Reston: National Council of Teachers of Mathematics.
Santos-Trigo, M. (2019). Mathematical problem solving and the use of digital technologies. In P. Liljedahl & M. Santos-Trigo (Eds.), Mathematical problem solving (pp. 63–89). Cham: Springer.
Strauss, A. L., & Corbin, J. (2008). Basics of qualitative research . Los Angeles: SAGE Publications.
Van de Walle, J., Karp, K., & Bay-Williams, J. (2015). Elementary and middle school mathematics—Teaching developmentally (9th ed.). New York: Pearson.
Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., & Wilensky, U. (2016). Defining computational thinking for mathematics and science classrooms. Journal of Science Education and Technology, 25 (1), 127–147. https://doi.org/10.1007/s10956-015-9581-5
Wilkerson-Jerde, M. H. (2014). Construction, categorization, and consensus: Student generated computational artifacts as a context for disciplinary reflection. Educational Technology Research and Development, 62 (1), 99–121.
Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49 (3), 33–35.
Yadav, A., Mayfield, C., Zhou, N., Hambrusch, S., & Korb, J. T. (2014). Computational thinking in elementary and secondary teacher education. ACM Transactions on Computing Education, 14 (1), 1–16.
Download references
Acknowledgements
This study was supported by the Chinese University of Hong Kong Faculty of Education Direct Grant (Ref. No. 4058081). The authors would like to thank the anonymous students who participated so enthusiastically in the study.
Author information
Authors and affiliations.
The Chinese University of Hong Kong, Shatin, Hong Kong SAR
Oi-Lam Ng & Zhihao Cui
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Oi-Lam Ng .
Additional information
Publisher's note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Reprints and permissions
About this article
Ng, OL., Cui, Z. Examining primary students’ mathematical problem-solving in a programming context: towards computationally enhanced mathematics education. ZDM Mathematics Education 53 , 847–860 (2021). https://doi.org/10.1007/s11858-020-01200-7
Download citation
Accepted : 23 October 2020
Published : 04 November 2020
Issue Date : August 2021
DOI : https://doi.org/10.1007/s11858-020-01200-7
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Problem-solving
- Computational thinking
- Constructionism
- Digital making
- Programming
- Mathematics education
- Find a journal
- Publish with us
- Track your research

IMAGES
COMMENTS
Project Euler is a series of challenging mathematical/computer programming problems that will require more than just mathematical insights to solve. Although mathematics will help you arrive at elegant and efficient methods, the use of a computer and programming skills will be required to solve most problems. The motivation for starting Project ...
Mathematical Programming in Practice5In management science, as in most sciences, there is a natura. interplay between theory andpractice. Theory provides tools for applied work and suggests viable approaches to problem solving, whereas practice adds focus to the theory by suggesting areas for theoretical development in its continual.
Our platform offers a range of essential problems for practice, as well as the latest questions being asked by top-tier companies. Explore; Problems; ... Interview. Store. problemset_primary. Study Plan. See all. Array 1722. String 717. Hash Table 621. Dynamic Programming 525. Math 513. Sorting 410. Greedy 375. Depth-First Search 295. Database ...
Guided interactive problem solving that's effective and fun. Master concepts in 15 minutes a day. Get started. Math. Data Analysis. Computer Science. Programming & AI. Science & Engineering. Join over 10 million people learning on Brilliant. Master concepts in 15 minutes a day.
This course is an introduction to linear optimization and its extensions emphasizing the underlying mathematical structures, geometrical ideas, algorithms and solutions of practical problems. The topics covered include: formulations, the geometry of linear optimization, duality theory, the simplex method, sensitivity analysis, robust optimization, large scale optimization network flows ...
Linear programming is a set of techniques used in mathematical programming, sometimes called mathematical optimization, ... The basic method for solving linear programming problems is called the simplex method, which has several variants. Another popular approach is the interior-point method.
To address this research gap, this study analyses the participants' thinking processes in solving programming-based mathematical problems from a flexibility perspective, focusing on the interplay between computational and mathematical thinking, that is, how CT and MT work together to influence and determine the problem-solver's choice of ...
Mathematical programming is a problem-solving approach that uses mathematical models and algorithms to optimize decision-making processes. Computer programming, on the other hand, is about writing code to create software or systems that computers can execute. While they both involve the word "programming," they have different focuses and ...
Mathematical programming refers to mathematical models used to solve problems such as decision problems. (Bruno Tisseyre et al., 2020) It involves a separation between the representation of the problem through a mathematical model and its solving. (Bruno Tisseyre et al., 2020) The solving may be done through general methods, such as branching methods, using the mathematical model designed to ...
Linear programming is a mathematical technique to solve problems involving finding maximums or minimums where a linear function is limited by various constraints. ... There are four steps that need to be completed when solving a problem using linear programming. They are as follows: Step 1: Compose an objective function to be minimized or ...
Project Euler is a series of challenging mathematical/computer programming problems that will require more than just mathematical insights to solve. Although mathematics will help you arrive at ...
Linear optimization problems with conditions requiring variables to be integers are called integer optimization problems. For the puzzle we are solving, thus, the correct model is: minimize y + z subject to: x + y + z = 32 2x + 4y + 8z = 80 x, y, z ≥ 0, integer. Below is a simple Python/SCIP program for solving it.
How Edabit Works. This is an introduction to how challenges on Edabit work. In the Code tab above you'll see a starter function that looks like this: function hello () { } All you have to do is type return "hello edabit.com" between the curly braces { } and then click the Check button. If you did this correctly, the button will turn red and ...
He defines problems and exercises through the lens of mathematical problem-solving, but they're applicable to programming as well. Each day we put our problem-solving skills to work as programmers: debugging code, learning a new topic, or even solving a problem. Exercises have their place, but as a programmer there's no replacement for ...
There are three main steps to this process: Create the conceptual mathematical model that captures the important resources and constraints in the business problem. Translate the conceptual mathematical model into a computer program that builds that model. Solve the mathematical model using a math programming solver.
Mathematical optimization (alternatively spelled optimisation) or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. [ 1 ] [ 2 ] It is generally divided into two subfields: discrete optimization and continuous optimization .
Dep. Informatics Engineering. 3030-290 Coimbra - Port ugal. +351 239 790000. [email protected]. ABSTRACT. Programming is hard to learn to most novice students. Several. reasons can be pointed out to ...
Join over 23 million developers in solving code challenges on HackerRank, one of the best ways to prepare for programming interviews.
The optimization techniques used to solve the problems are primarily linear, mixed-integer linear, nonlinear, and mixed integer nonlinear programming. The book also covers important considerations for solving real-world optimization problems, such as dealing with valid inequalities and symmetry during the modeling phase, but also data ...
Fundamental concepts of mathematical modeling Modeling is one of the most effective, commonly used tools in engineering and the applied sciences. In this book, the authors deal with mathematical programming models both linear and nonlinear and across a wide range of practical applications. Whereas other books concentrate on standard methods of analysis, the authors focus on the power of ...
In summary, here are 10 of our most popular problem solving courses. Effective Problem-Solving and Decision-Making: University of California, Irvine. Creative Thinking: Techniques and Tools for Success: Imperial College London. Solving Complex Problems: Macquarie University. Solving Problems with Creative and Critical Thinking: IBM.
This paper reports on a design-based study within the context of a 3-day digital making (DM) summer camp attended by a group of students (aged 11-13) in grades 5 and 6. During the camp, students were presented with a set of mathematical problems to solve in a block-based programming environment, which was connected to various physical input sensors and output devices (e.g., push buttons, LED ...
5.1: Problem Solving An introduction to problem-solving is the process of identifying a challenge or obstacle and finding an effective solution through a systematic approach. It involves critical thinking, analyzing the problem, devising a plan, implementing it, and reflecting on the outcome to ensure the problem is resolved.
amining primar students' mathematical problem-solving in a programming context: towards… 849 1 3 Examples of common software-hardware combinations with DM capabilities include Micro:bit and Arduino, the latter of which was used in this study. Despite widespread recognition that making is benecial
Works with the team to mine data using modern tools and programming languages. Develops algorithms, performs small scale experimentation, builds data driven applications to translate data into intelligence, and develops solutions for solving business problems. Incorporates predictive modeling, statistics and other analysis techniques for collecting, exploring, interpreting and extracting ...