
Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

7 Module 7: Thinking, Reasoning, and Problem-Solving
This module is about how a solid working knowledge of psychological principles can help you to think more effectively, so you can succeed in school and life. You might be inclined to believe that—because you have been thinking for as long as you can remember, because you are able to figure out the solution to many problems, because you feel capable of using logic to argue a point, because you can evaluate whether the things you read and hear make sense—you do not need any special training in thinking. But this, of course, is one of the key barriers to helping people think better. If you do not believe that there is anything wrong, why try to fix it?
The human brain is indeed a remarkable thinking machine, capable of amazing, complex, creative, logical thoughts. Why, then, are we telling you that you need to learn how to think? Mainly because one major lesson from cognitive psychology is that these capabilities of the human brain are relatively infrequently realized. Many psychologists believe that people are essentially “cognitive misers.” It is not that we are lazy, but that we have a tendency to expend the least amount of mental effort necessary. Although you may not realize it, it actually takes a great deal of energy to think. Careful, deliberative reasoning and critical thinking are very difficult. Because we seem to be successful without going to the trouble of using these skills well, it feels unnecessary to develop them. As you shall see, however, there are many pitfalls in the cognitive processes described in this module. When people do not devote extra effort to learning and improving reasoning, problem solving, and critical thinking skills, they make many errors.
As is true for memory, if you develop the cognitive skills presented in this module, you will be more successful in school. It is important that you realize, however, that these skills will help you far beyond school, even more so than a good memory will. Although it is somewhat useful to have a good memory, ten years from now no potential employer will care how many questions you got right on multiple choice exams during college. All of them will, however, recognize whether you are a logical, analytical, critical thinker. With these thinking skills, you will be an effective, persuasive communicator and an excellent problem solver.
The module begins by describing different kinds of thought and knowledge, especially conceptual knowledge and critical thinking. An understanding of these differences will be valuable as you progress through school and encounter different assignments that require you to tap into different kinds of knowledge. The second section covers deductive and inductive reasoning, which are processes we use to construct and evaluate strong arguments. They are essential skills to have whenever you are trying to persuade someone (including yourself) of some point, or to respond to someone’s efforts to persuade you. The module ends with a section about problem-solving. A solid understanding of the key processes involved in problem-solving will help you to handle many daily challenges.
7.1. Different kinds of thought
7.2. Reasoning and Judgment
7.3. Problem Solving
READING WITH PURPOSE
Remember and understand.
By reading and studying Module 7, you should be able to remember and describe:
- Concepts and inferences (7.1)
- Procedural knowledge (7.1)
- Metacognition (7.1)
- Characteristics of critical thinking: skepticism; identify biases, distortions, omissions, and assumptions; reasoning and problem-solving skills (7.1)
- Reasoning: deductive reasoning, deductively valid argument, inductive reasoning, inductively strong argument, availability heuristic, representativeness heuristic (7.2)
- Fixation: functional fixedness, mental set (7.3)
- Algorithms, heuristics, and the role of confirmation bias (7.3)
- Effective problem-solving sequence (7.3)
By reading and thinking about how the concepts in Module 7 apply to real life, you should be able to:
- Identify which type of knowledge a piece of information is (7.1)
- Recognize examples of deductive and inductive reasoning (7.2)
- Recognize judgments that have probably been influenced by the availability heuristic (7.2)
- Recognize examples of problem-solving heuristics and algorithms (7.3)
Analyze, Evaluate, and Create
By reading and thinking about Module 7, participating in classroom activities, and completing out-of-class assignments, you should be able to:
- Use the principles of critical thinking to evaluate information (7.1)
- Explain whether examples of reasoning arguments are deductively valid or inductively strong (7.2)
- Outline how you could try to solve a problem from your life using the effective problem-solving sequence (7.3)
7.1. Different kinds of thought and knowledge
- Take a few minutes to write down everything that you know about dogs.
- Do you believe that:
- Psychic ability exists?
- Hypnosis is an altered state of consciousness?
- Magnet therapy is effective for relieving pain?
- Aerobic exercise is an effective treatment for depression?
- UFO’s from outer space have visited earth?
On what do you base your belief or disbelief for the questions above?
Of course, we all know what is meant by the words think and knowledge . You probably also realize that they are not unitary concepts; there are different kinds of thought and knowledge. In this section, let us look at some of these differences. If you are familiar with these different kinds of thought and pay attention to them in your classes, it will help you to focus on the right goals, learn more effectively, and succeed in school. Different assignments and requirements in school call on you to use different kinds of knowledge or thought, so it will be very helpful for you to learn to recognize them (Anderson, et al. 2001).
Factual and conceptual knowledge
Module 5 introduced the idea of declarative memory, which is composed of facts and episodes. If you have ever played a trivia game or watched Jeopardy on TV, you realize that the human brain is able to hold an extraordinary number of facts. Likewise, you realize that each of us has an enormous store of episodes, essential facts about events that happened in our own lives. It may be difficult to keep that in mind when we are struggling to retrieve one of those facts while taking an exam, however. Part of the problem is that, in contradiction to the advice from Module 5, many students continue to try to memorize course material as a series of unrelated facts (picture a history student simply trying to memorize history as a set of unrelated dates without any coherent story tying them together). Facts in the real world are not random and unorganized, however. It is the way that they are organized that constitutes a second key kind of knowledge, conceptual.
Concepts are nothing more than our mental representations of categories of things in the world. For example, think about dogs. When you do this, you might remember specific facts about dogs, such as they have fur and they bark. You may also recall dogs that you have encountered and picture them in your mind. All of this information (and more) makes up your concept of dog. You can have concepts of simple categories (e.g., triangle), complex categories (e.g., small dogs that sleep all day, eat out of the garbage, and bark at leaves), kinds of people (e.g., psychology professors), events (e.g., birthday parties), and abstract ideas (e.g., justice). Gregory Murphy (2002) refers to concepts as the “glue that holds our mental life together” (p. 1). Very simply, summarizing the world by using concepts is one of the most important cognitive tasks that we do. Our conceptual knowledge is our knowledge about the world. Individual concepts are related to each other to form a rich interconnected network of knowledge. For example, think about how the following concepts might be related to each other: dog, pet, play, Frisbee, chew toy, shoe. Or, of more obvious use to you now, how these concepts are related: working memory, long-term memory, declarative memory, procedural memory, and rehearsal? Because our minds have a natural tendency to organize information conceptually, when students try to remember course material as isolated facts, they are working against their strengths.
One last important point about concepts is that they allow you to instantly know a great deal of information about something. For example, if someone hands you a small red object and says, “here is an apple,” they do not have to tell you, “it is something you can eat.” You already know that you can eat it because it is true by virtue of the fact that the object is an apple; this is called drawing an inference, assuming that something is true on the basis of your previous knowledge (for example, of category membership or of how the world works) or logical reasoning.
Procedural knowledge
Physical skills, such as tying your shoes, doing a cartwheel, and driving a car (or doing all three at the same time, but don’t try this at home) are certainly a kind of knowledge. They are procedural knowledge, the same idea as procedural memory that you saw in Module 5. Mental skills, such as reading, debating, and planning a psychology experiment, are procedural knowledge, as well. In short, procedural knowledge is the knowledge how to do something (Cohen & Eichenbaum, 1993).
Metacognitive knowledge
Floyd used to think that he had a great memory. Now, he has a better memory. Why? Because he finally realized that his memory was not as great as he once thought it was. Because Floyd eventually learned that he often forgets where he put things, he finally developed the habit of putting things in the same place. (Unfortunately, he did not learn this lesson before losing at least 5 watches and a wedding ring.) Because he finally realized that he often forgets to do things, he finally started using the To Do list app on his phone. And so on. Floyd’s insights about the real limitations of his memory have allowed him to remember things that he used to forget.
All of us have knowledge about the way our own minds work. You may know that you have a good memory for people’s names and a poor memory for math formulas. Someone else might realize that they have difficulty remembering to do things, like stopping at the store on the way home. Others still know that they tend to overlook details. This knowledge about our own thinking is actually quite important; it is called metacognitive knowledge, or metacognition . Like other kinds of thinking skills, it is subject to error. For example, in unpublished research, one of the authors surveyed about 120 General Psychology students on the first day of the term. Among other questions, the students were asked them to predict their grade in the class and report their current Grade Point Average. Two-thirds of the students predicted that their grade in the course would be higher than their GPA. (The reality is that at our college, students tend to earn lower grades in psychology than their overall GPA.) Another example: Students routinely report that they thought they had done well on an exam, only to discover, to their dismay, that they were wrong (more on that important problem in a moment). Both errors reveal a breakdown in metacognition.
The Dunning-Kruger Effect
In general, most college students probably do not study enough. For example, using data from the National Survey of Student Engagement, Fosnacht et al. (2018) reported that first-year students at 4-year colleges in the U.S. averaged less than 14 hours per week preparing for classes. The typical suggestion is that you should spend two hours outside of class for every hour in class, or 24 – 30 hours per week for a full-time student. Clearly, students generally are nowhere near that recommended mark. Many observers, including some faculty, believe that this shortfall is a result of students being too busy or lazy. Now, it may be true that many students are too busy, with work and family obligations, for example. Others are not particularly motivated in school, and therefore might correctly be labeled lazy. A third possible explanation, however, is that some students might not think they need to spend this much time. And this is a matter of metacognition. Consider the scenario that we mentioned above, students thinking they had done well on an exam only to discover that they did not. Justin Kruger and David Dunning examined scenarios very much like this in 1999. Kruger and Dunning gave research participants tests measuring humor, logic, and grammar. Then, they asked the participants to assess their own abilities and test performance in these areas. They found that participants generally tended to overestimate their abilities, already a problem with metacognition. Importantly, the participants who scored the lowest overestimated their abilities the most. Specifically, students who scored in the bottom quarter (averaging in the 12th percentile) thought they had scored in the 62nd percentile. This has become known as the Dunning-Kruger effect . Many individual faculty members have replicated these results with their own students on their course exams, including the authors of this book. Think about it. Some students who just took an exam and performed poorly believe that they did well before seeing their score. It seems very likely that these are the very same students who stopped studying the night before because they thought they were “done.” Quite simply, it is not just that they did not know the material. They did not know that they did not know the material. That is poor metacognition.
In order to develop good metacognitive skills, you should continually monitor your thinking and seek frequent feedback on the accuracy of your thinking (Medina et al., 2017). For example, in classes get in the habit of predicting your exam grades. As soon as possible after taking an exam, try to find out which questions you missed and try to figure out why. If you do this soon enough, you may be able to recall the way it felt when you originally answered the question. Did you feel confident that you had answered the question correctly? Then you have just discovered an opportunity to improve your metacognition. Be on the lookout for that feeling and respond with caution.
concept: a mental representation of a category of things in the world
Dunning-Kruger effect : individuals who are less competent tend to overestimate their abilities more than individuals who are more competent do
inference: an assumption about the truth of something that is not stated. Inferences come from our prior knowledge and experience, and from logical reasoning
metacognition: knowledge about one’s own cognitive processes; thinking about your thinking
Critical thinking
One particular kind of knowledge or thinking skill that is related to metacognition is critical thinking (Chew, 2020). You may have noticed that critical thinking is an objective in many college courses, and thus it could be a legitimate topic to cover in nearly any college course. It is particularly appropriate in psychology, however. As the science of (behavior and) mental processes, psychology is obviously well suited to be the discipline through which you should be introduced to this important way of thinking.
More importantly, there is a particular need to use critical thinking in psychology. We are all, in a way, experts in human behavior and mental processes, having engaged in them literally since birth. Thus, perhaps more than in any other class, students typically approach psychology with very clear ideas and opinions about its subject matter. That is, students already “know” a lot about psychology. The problem is, “it ain’t so much the things we don’t know that get us into trouble. It’s the things we know that just ain’t so” (Ward, quoted in Gilovich 1991). Indeed, many of students’ preconceptions about psychology are just plain wrong. Randolph Smith (2002) wrote a book about critical thinking in psychology called Challenging Your Preconceptions, highlighting this fact. On the other hand, many of students’ preconceptions about psychology are just plain right! But wait, how do you know which of your preconceptions are right and which are wrong? And when you come across a research finding or theory in this class that contradicts your preconceptions, what will you do? Will you stick to your original idea, discounting the information from the class? Will you immediately change your mind? Critical thinking can help us sort through this confusing mess.
But what is critical thinking? The goal of critical thinking is simple to state (but extraordinarily difficult to achieve): it is to be right, to draw the correct conclusions, to believe in things that are true and to disbelieve things that are false. We will provide two definitions of critical thinking (or, if you like, one large definition with two distinct parts). First, a more conceptual one: Critical thinking is thinking like a scientist in your everyday life (Schmaltz et al., 2017). Our second definition is more operational; it is simply a list of skills that are essential to be a critical thinker. Critical thinking entails solid reasoning and problem-solving skills; skepticism; and an ability to identify biases, distortions, omissions, and assumptions. Excellent deductive and inductive reasoning, and problem-solving skills contribute to critical thinking. So, you can consider the subject matter of sections 7.2 and 7.3 to be part of critical thinking. Because we will be devoting considerable time to these concepts in the rest of the module, let us begin with a discussion about the other aspects of critical thinking.
Let’s address that first part of the definition. Scientists form hypotheses, or predictions, about some possible future observations. Then, they collect data or information (think of this as making those future observations). They do their best to make unbiased observations using reliable techniques that have been verified by others. Then, and only then, they draw a conclusion about what those observations mean. Oh, and do not forget the most important part. “Conclusion” is probably not the most appropriate word because this conclusion is only tentative. A scientist is always prepared that someone else might come along and produce new observations that would require a new conclusion to be drawn. Wow! If you like to be right, you could do a lot worse than using a process like this.
A Critical Thinker’s Toolkit
Now for the second part of the definition. Good critical thinkers (and scientists) rely on a variety of tools to evaluate information. Perhaps the most recognizable tool for critical thinking is skepticism (and this term provides the clearest link to the thinking like a scientist definition, as you are about to see). Some people intend it as an insult when they call someone a skeptic. But if someone calls you a skeptic, if they are using the term correctly, you should consider it a great compliment. Simply put, skepticism is a way of thinking in which you refrain from drawing a conclusion or changing your mind until good evidence has been provided. People from Missouri should recognize this principle, as Missouri is known as the Show-Me State. As a skeptic, you are not inclined to believe something just because someone said so, because someone else believes it, or because it sounds reasonable. You must be persuaded by high-quality evidence.
Of course, if that evidence is produced, you have a responsibility as a skeptic to change your belief. Failure to change a belief in the face of good evidence is not skepticism; skepticism has open-mindedness at its core. M. Neil Browne and Stuart Keeley (2018) use the term weak sense critical thinking to describe critical thinking behaviors that are used only to strengthen a prior belief. Strong sense critical thinking, on the other hand, has as its goal reaching the best conclusion. Sometimes that means strengthening your prior belief, but sometimes it means changing your belief to accommodate the better evidence.
Many times, a failure to think critically or a weak sense of critical thinking is related to a bias , an inclination, tendency, leaning, or prejudice. Everybody has biases, but many people are unaware of them. Awareness of your own biases gives you the opportunity to control or counteract them. Unfortunately, however, many people are happy to let their biases creep into their attempts to persuade others; indeed, it is a key part of their persuasive strategy. To see how these biases influence messages, just look at the different descriptions and explanations of the same events given by people of different ages or income brackets, or conservative versus liberal commentators, or by commentators from different parts of the world. Of course, to be successful, these people who are consciously using their biases must disguise them. Even undisguised biases can be difficult to identify, so disguised ones can be nearly impossible.
Here are some common sources of biases:
- Personal values and beliefs. Some people believe that human beings are basically driven to seek power and that they are typically in competition with one another over scarce resources. These beliefs are similar to the world-view that political scientists call “realism.” Other people believe that human beings prefer to cooperate and that, given the chance, they will do so. These beliefs are similar to the world-view known as “idealism.” For many people, these deeply held beliefs can influence, or bias, their interpretations of such wide-ranging situations as the behavior of nations and their leaders or the behavior of the driver in the car ahead of you. For example, if your worldview is that people are typically in competition and someone cuts you off on the highway, you may assume that the driver did it purposely to get ahead of you. Other types of beliefs about the way the world is or the way the world should be, for example, political beliefs, can similarly become a significant source of bias.
- Racism, sexism, ageism and other forms of prejudice and bigotry. These are, sadly, a common source of bias in many people. They are essentially a special kind of “belief about the way the world is.” These beliefs—for example, that women do not make effective leaders—lead people to ignore contradictory evidence (examples of effective women leaders, or research that disputes the belief) and to interpret ambiguous evidence in a way consistent with the belief.
- Self-interest. When particular people benefit from things turning out a certain way, they can sometimes be very susceptible to letting that interest bias them. For example, a company that will earn a profit if they sell their product may have a bias in the way that they give information about their product. A union that will benefit if its members get a generous contract might have a bias in the way it presents information about salaries at competing organizations. (Note that our inclusion of examples describing both companies and unions is an explicit attempt to control for our own personal biases). Homebuyers are often dismayed to discover that they purchased their dream house from someone whose self-interest led them to lie about flooding problems in the basement or back yard. This principle, the biasing power of self-interest, is likely what led to the famous phrase Caveat Emptor (let the buyer beware) .
Knowing that these types of biases exist will help you evaluate evidence more critically. Do not forget, though, that people are not always keen to let you discover the sources of biases in their arguments. For example, companies or political organizations can disguise their support of a research study by contracting with a university professor, who comes complete with a seemingly unbiased institutional affiliation, to conduct the study.
People’s biases, conscious or unconscious, can lead them to make omissions, distortions, and assumptions that undermine our ability to correctly evaluate evidence. It is essential that you look for these elements. Always ask, what is missing, what is not as it appears, and what is being assumed here? For example, consider this (fictional) chart from an ad reporting customer satisfaction at 4 local health clubs.
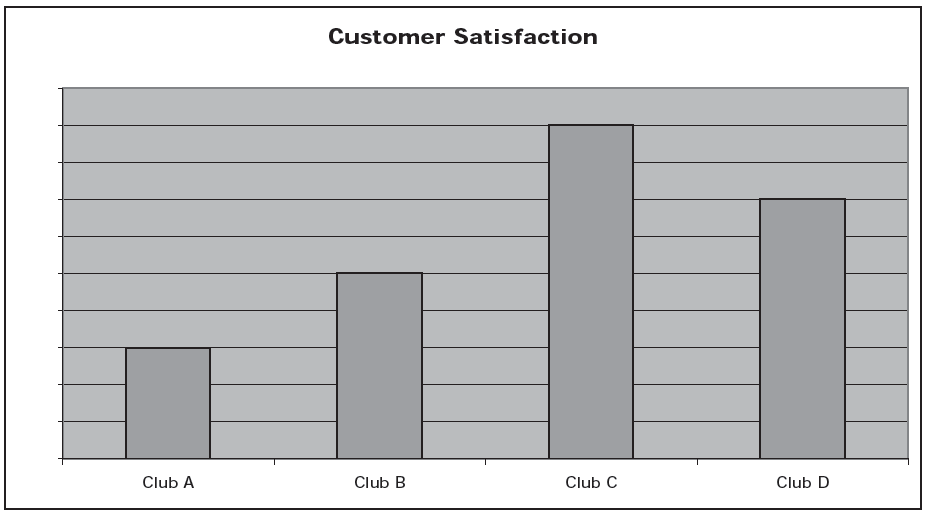
Clearly, from the results of the chart, one would be tempted to give Club C a try, as customer satisfaction is much higher than for the other 3 clubs.
There are so many distortions and omissions in this chart, however, that it is actually quite meaningless. First, how was satisfaction measured? Do the bars represent responses to a survey? If so, how were the questions asked? Most importantly, where is the missing scale for the chart? Although the differences look quite large, are they really?
Well, here is the same chart, with a different scale, this time labeled:
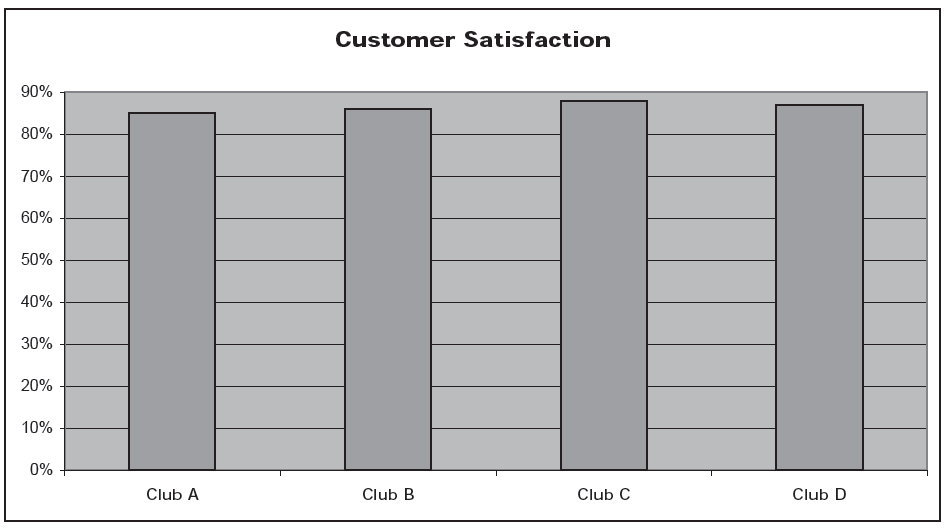
Club C is not so impressive anymore, is it? In fact, all of the health clubs have customer satisfaction ratings (whatever that means) between 85% and 88%. In the first chart, the entire scale of the graph included only the percentages between 83 and 89. This “judicious” choice of scale—some would call it a distortion—and omission of that scale from the chart make the tiny differences among the clubs seem important, however.
Also, in order to be a critical thinker, you need to learn to pay attention to the assumptions that underlie a message. Let us briefly illustrate the role of assumptions by touching on some people’s beliefs about the criminal justice system in the US. Some believe that a major problem with our judicial system is that many criminals go free because of legal technicalities. Others believe that a major problem is that many innocent people are convicted of crimes. The simple fact is, both types of errors occur. A person’s conclusion about which flaw in our judicial system is the greater tragedy is based on an assumption about which of these is the more serious error (letting the guilty go free or convicting the innocent). This type of assumption is called a value assumption (Browne and Keeley, 2018). It reflects the differences in values that people develop, differences that may lead us to disregard valid evidence that does not fit in with our particular values.
Oh, by the way, some students probably noticed this, but the seven tips for evaluating information that we shared in Module 1 are related to this. Actually, they are part of this section. The tips are, to a very large degree, a set of ideas you can use to help you identify biases, distortions, omissions, and assumptions. If you do not remember this section, we strongly recommend you take a few minutes to review it.
skepticism: a way of thinking in which you refrain from drawing a conclusion or changing your mind until good evidence has been provided
bias: an inclination, tendency, leaning, or prejudice
- Which of your beliefs (or disbeliefs) from the Activate exercise for this section were derived from a process of critical thinking? If some of your beliefs were not based on critical thinking, are you willing to reassess these beliefs? If the answer is no, why do you think that is? If the answer is yes, what concrete steps will you take?
7.2 Reasoning and Judgment
- What percentage of kidnappings are committed by strangers?
- Which area of the house is riskiest: kitchen, bathroom, or stairs?
- What is the most common cancer in the US?
- What percentage of workplace homicides are committed by co-workers?
An essential set of procedural thinking skills is reasoning , the ability to generate and evaluate solid conclusions from a set of statements or evidence. You should note that these conclusions (when they are generated instead of being evaluated) are one key type of inference that we described in Section 7.1. There are two main types of reasoning, deductive and inductive.
Deductive reasoning
Suppose your teacher tells you that if you get an A on the final exam in a course, you will get an A for the whole course. Then, you get an A on the final exam. What will your final course grade be? Most people can see instantly that you can conclude with certainty that you will get an A for the course. This is a type of reasoning called deductive reasoning , which is defined as reasoning in which a conclusion is guaranteed to be true as long as the statements leading to it are true. The three statements can be listed as an argument , with two beginning statements and a conclusion:
Statement 1: If you get an A on the final exam, you will get an A for the course
Statement 2: You get an A on the final exam
Conclusion: You will get an A for the course
This particular arrangement, in which true beginning statements lead to a guaranteed true conclusion, is known as a deductively valid argument . Although deductive reasoning is often the subject of abstract, brain-teasing, puzzle-like word problems, it is actually an extremely important type of everyday reasoning. It is just hard to recognize sometimes. For example, imagine that you are looking for your car keys and you realize that they are either in the kitchen drawer or in your bookbag. After looking in the kitchen drawer, you instantly know that they must be in your bookbag. That conclusion results from a simple deductive reasoning argument. In addition, solid deductive reasoning skills are necessary for you to succeed in the sciences, philosophy, math, computer programming, and any endeavor involving the use of logic to persuade others to your point of view or to evaluate others’ arguments.
Cognitive psychologists, and before them philosophers, have been quite interested in deductive reasoning, not so much for its practical applications, but for the insights it can offer them about the ways that human beings think. One of the early ideas to emerge from the examination of deductive reasoning is that people learn (or develop) mental versions of rules that allow them to solve these types of reasoning problems (Braine, 1978; Braine, Reiser, & Rumain, 1984). The best way to see this point of view is to realize that there are different possible rules, and some of them are very simple. For example, consider this rule of logic:
therefore q
Logical rules are often presented abstractly, as letters, in order to imply that they can be used in very many specific situations. Here is a concrete version of the of the same rule:
I’ll either have pizza or a hamburger for dinner tonight (p or q)
I won’t have pizza (not p)
Therefore, I’ll have a hamburger (therefore q)
This kind of reasoning seems so natural, so easy, that it is quite plausible that we would use a version of this rule in our daily lives. At least, it seems more plausible than some of the alternative possibilities—for example, that we need to have experience with the specific situation (pizza or hamburger, in this case) in order to solve this type of problem easily. So perhaps there is a form of natural logic (Rips, 1990) that contains very simple versions of logical rules. When we are faced with a reasoning problem that maps onto one of these rules, we use the rule.
But be very careful; things are not always as easy as they seem. Even these simple rules are not so simple. For example, consider the following rule. Many people fail to realize that this rule is just as valid as the pizza or hamburger rule above.
if p, then q
therefore, not p
Concrete version:
If I eat dinner, then I will have dessert
I did not have dessert
Therefore, I did not eat dinner
The simple fact is, it can be very difficult for people to apply rules of deductive logic correctly; as a result, they make many errors when trying to do so. Is this a deductively valid argument or not?
Students who like school study a lot
Students who study a lot get good grades
Jane does not like school
Therefore, Jane does not get good grades
Many people are surprised to discover that this is not a logically valid argument; the conclusion is not guaranteed to be true from the beginning statements. Although the first statement says that students who like school study a lot, it does NOT say that students who do not like school do not study a lot. In other words, it may very well be possible to study a lot without liking school. Even people who sometimes get problems like this right might not be using the rules of deductive reasoning. Instead, they might just be making judgments for examples they know, in this case, remembering instances of people who get good grades despite not liking school.
Making deductive reasoning even more difficult is the fact that there are two important properties that an argument may have. One, it can be valid or invalid (meaning that the conclusion does or does not follow logically from the statements leading up to it). Two, an argument (or more correctly, its conclusion) can be true or false. Here is an example of an argument that is logically valid, but has a false conclusion (at least we think it is false).
Either you are eleven feet tall or the Grand Canyon was created by a spaceship crashing into the earth.
You are not eleven feet tall
Therefore the Grand Canyon was created by a spaceship crashing into the earth
This argument has the exact same form as the pizza or hamburger argument above, making it is deductively valid. The conclusion is so false, however, that it is absurd (of course, the reason the conclusion is false is that the first statement is false). When people are judging arguments, they tend to not observe the difference between deductive validity and the empirical truth of statements or conclusions. If the elements of an argument happen to be true, people are likely to judge the argument logically valid; if the elements are false, they will very likely judge it invalid (Markovits & Bouffard-Bouchard, 1992; Moshman & Franks, 1986). Thus, it seems a stretch to say that people are using these logical rules to judge the validity of arguments. Many psychologists believe that most people actually have very limited deductive reasoning skills (Johnson-Laird, 1999). They argue that when faced with a problem for which deductive logic is required, people resort to some simpler technique, such as matching terms that appear in the statements and the conclusion (Evans, 1982). This might not seem like a problem, but what if reasoners believe that the elements are true and they happen to be wrong; they will believe that they are using a form of reasoning that guarantees they are correct and yet be wrong.
reasoning , the ability to generate and evaluate solid conclusions from a set of statements or evidence
deductive reasoning: a type of reasoning in which the conclusion is guaranteed to be true any time the statements leading up to it are true
argument: a set of statements in which the beginning statements lead to a conclusion
deductively valid argument: an argument for which true beginning statements guarantee that the conclusion is true
Inductive reasoning and judgment
Every day, you make many judgments about the likelihood of one thing or another. Whether you realize it or not, you are practicing inductive reasoning on a daily basis. In inductive reasoning arguments, a conclusion is likely whenever the statements preceding it are true. The first thing to notice about inductive reasoning is that, by definition, you can never be sure about your conclusion; you can only estimate how likely the conclusion is. Inductive reasoning may lead you to focus on Memory Encoding and Recoding when you study for the exam, but it is possible the instructor will ask more questions about Memory Retrieval instead. Unlike deductive reasoning, the conclusions you reach through inductive reasoning are only probable, not certain. That is why scientists consider inductive reasoning weaker than deductive reasoning. But imagine how hard it would be for us to function if we could not act unless we were certain about the outcome.
Inductive reasoning can be represented as logical arguments consisting of statements and a conclusion, just as deductive reasoning can be. In an inductive argument, you are given some statements and a conclusion (or you are given some statements and must draw a conclusion). An argument is inductively strong if the conclusion would be very probable whenever the statements are true. So, for example, here is an inductively strong argument:
- Statement #1: The forecaster on Channel 2 said it is going to rain today.
- Statement #2: The forecaster on Channel 5 said it is going to rain today.
- Statement #3: It is very cloudy and humid.
- Statement #4: You just heard thunder.
- Conclusion (or judgment): It is going to rain today.
Think of the statements as evidence, on the basis of which you will draw a conclusion. So, based on the evidence presented in the four statements, it is very likely that it will rain today. Will it definitely rain today? Certainly not. We can all think of times that the weather forecaster was wrong.
A true story: Some years ago psychology student was watching a baseball playoff game between the St. Louis Cardinals and the Los Angeles Dodgers. A graphic on the screen had just informed the audience that the Cardinal at bat, (Hall of Fame shortstop) Ozzie Smith, a switch hitter batting left-handed for this plate appearance, had never, in nearly 3000 career at-bats, hit a home run left-handed. The student, who had just learned about inductive reasoning in his psychology class, turned to his companion (a Cardinals fan) and smugly said, “It is an inductively strong argument that Ozzie Smith will not hit a home run.” He turned back to face the television just in time to watch the ball sail over the right-field fence for a home run. Although the student felt foolish at the time, he was not wrong. It was an inductively strong argument; 3000 at-bats is an awful lot of evidence suggesting that the Wizard of Ozz (as he was known) would not be hitting one out of the park (think of each at-bat without a home run as a statement in an inductive argument). Sadly (for the die-hard Cubs fan and Cardinals-hating student), despite the strength of the argument, the conclusion was wrong.
Given the possibility that we might draw an incorrect conclusion even with an inductively strong argument, we really want to be sure that we do, in fact, make inductively strong arguments. If we judge something probable, it had better be probable. If we judge something nearly impossible, it had better not happen. Think of inductive reasoning, then, as making reasonably accurate judgments of the probability of some conclusion given a set of evidence.
We base many decisions in our lives on inductive reasoning. For example:
Statement #1: Psychology is not my best subject
Statement #2: My psychology instructor has a reputation for giving difficult exams
Statement #3: My first psychology exam was much harder than I expected
Judgment: The next exam will probably be very difficult.
Decision: I will study tonight instead of watching Netflix.
Some other examples of judgments that people commonly make in a school context include judgments of the likelihood that:
- A particular class will be interesting/useful/difficult
- You will be able to finish writing a paper by next week if you go out tonight
- Your laptop’s battery will last through the next trip to the library
- You will not miss anything important if you skip class tomorrow
- Your instructor will not notice if you skip class tomorrow
- You will be able to find a book that you will need for a paper
- There will be an essay question about Memory Encoding on the next exam
Tversky and Kahneman (1983) recognized that there are two general ways that we might make these judgments; they termed them extensional (i.e., following the laws of probability) and intuitive (i.e., using shortcuts or heuristics, see below). We will use a similar distinction between Type 1 and Type 2 thinking, as described by Keith Stanovich and his colleagues (Evans and Stanovich, 2013; Stanovich and West, 2000). Type 1 thinking is fast, automatic, effortless, and emotional. In fact, it is hardly fair to call it reasoning at all, as judgments just seem to pop into one’s head. Type 2 thinking , on the other hand, is slow, effortful, and logical. So obviously, it is more likely to lead to a correct judgment, or an optimal decision. The problem is, we tend to over-rely on Type 1. Now, we are not saying that Type 2 is the right way to go for every decision or judgment we make. It seems a bit much, for example, to engage in a step-by-step logical reasoning procedure to decide whether we will have chicken or fish for dinner tonight.
Many bad decisions in some very important contexts, however, can be traced back to poor judgments of the likelihood of certain risks or outcomes that result from the use of Type 1 when a more logical reasoning process would have been more appropriate. For example:
Statement #1: It is late at night.
Statement #2: Albert has been drinking beer for the past five hours at a party.
Statement #3: Albert is not exactly sure where he is or how far away home is.
Judgment: Albert will have no difficulty walking home.
Decision: He walks home alone.
As you can see in this example, the three statements backing up the judgment do not really support it. In other words, this argument is not inductively strong because it is based on judgments that ignore the laws of probability. What are the chances that someone facing these conditions will be able to walk home alone easily? And one need not be drunk to make poor decisions based on judgments that just pop into our heads.
The truth is that many of our probability judgments do not come very close to what the laws of probability say they should be. Think about it. In order for us to reason in accordance with these laws, we would need to know the laws of probability, which would allow us to calculate the relationship between particular pieces of evidence and the probability of some outcome (i.e., how much likelihood should change given a piece of evidence), and we would have to do these heavy math calculations in our heads. After all, that is what Type 2 requires. Needless to say, even if we were motivated, we often do not even know how to apply Type 2 reasoning in many cases.
So what do we do when we don’t have the knowledge, skills, or time required to make the correct mathematical judgment? Do we hold off and wait until we can get better evidence? Do we read up on probability and fire up our calculator app so we can compute the correct probability? Of course not. We rely on Type 1 thinking. We “wing it.” That is, we come up with a likelihood estimate using some means at our disposal. Psychologists use the term heuristic to describe the type of “winging it” we are talking about. A heuristic is a shortcut strategy that we use to make some judgment or solve some problem (see Section 7.3). Heuristics are easy and quick, think of them as the basic procedures that are characteristic of Type 1. They can absolutely lead to reasonably good judgments and decisions in some situations (like choosing between chicken and fish for dinner). They are, however, far from foolproof. There are, in fact, quite a lot of situations in which heuristics can lead us to make incorrect judgments, and in many cases, the decisions based on those judgments can have serious consequences.
Let us return to the activity that begins this section. You were asked to judge the likelihood (or frequency) of certain events and risks. You were free to come up with your own evidence (or statements) to make these judgments. This is where a heuristic crops up. As a judgment shortcut, we tend to generate specific examples of those very events to help us decide their likelihood or frequency. For example, if we are asked to judge how common, frequent, or likely a particular type of cancer is, many of our statements would be examples of specific cancer cases:
Statement #1: Andy Kaufman (comedian) had lung cancer.
Statement #2: Colin Powell (US Secretary of State) had prostate cancer.
Statement #3: Bob Marley (musician) had skin and brain cancer
Statement #4: Sandra Day O’Connor (Supreme Court Justice) had breast cancer.
Statement #5: Fred Rogers (children’s entertainer) had stomach cancer.
Statement #6: Robin Roberts (news anchor) had breast cancer.
Statement #7: Bette Davis (actress) had breast cancer.
Judgment: Breast cancer is the most common type.
Your own experience or memory may also tell you that breast cancer is the most common type. But it is not (although it is common). Actually, skin cancer is the most common type in the US. We make the same types of misjudgments all the time because we do not generate the examples or evidence according to their actual frequencies or probabilities. Instead, we have a tendency (or bias) to search for the examples in memory; if they are easy to retrieve, we assume that they are common. To rephrase this in the language of the heuristic, events seem more likely to the extent that they are available to memory. This bias has been termed the availability heuristic (Kahneman and Tversky, 1974).
The fact that we use the availability heuristic does not automatically mean that our judgment is wrong. The reason we use heuristics in the first place is that they work fairly well in many cases (and, of course, that they are easy to use). So, the easiest examples to think of sometimes are the most common ones. Is it more likely that a member of the U.S. Senate is a man or a woman? Most people have a much easier time generating examples of male senators. And as it turns out, the U.S. Senate has many more men than women (74 to 26 in 2020). In this case, then, the availability heuristic would lead you to make the correct judgment; it is far more likely that a senator would be a man.
In many other cases, however, the availability heuristic will lead us astray. This is because events can be memorable for many reasons other than their frequency. Section 5.2, Encoding Meaning, suggested that one good way to encode the meaning of some information is to form a mental image of it. Thus, information that has been pictured mentally will be more available to memory. Indeed, an event that is vivid and easily pictured will trick many people into supposing that type of event is more common than it actually is. Repetition of information will also make it more memorable. So, if the same event is described to you in a magazine, on the evening news, on a podcast that you listen to, and in your Facebook feed; it will be very available to memory. Again, the availability heuristic will cause you to misperceive the frequency of these types of events.
Most interestingly, information that is unusual is more memorable. Suppose we give you the following list of words to remember: box, flower, letter, platypus, oven, boat, newspaper, purse, drum, car. Very likely, the easiest word to remember would be platypus, the unusual one. The same thing occurs with memories of events. An event may be available to memory because it is unusual, yet the availability heuristic leads us to judge that the event is common. Did you catch that? In these cases, the availability heuristic makes us think the exact opposite of the true frequency. We end up thinking something is common because it is unusual (and therefore memorable). Yikes.
The misapplication of the availability heuristic sometimes has unfortunate results. For example, if you went to K-12 school in the US over the past 10 years, it is extremely likely that you have participated in lockdown and active shooter drills. Of course, everyone is trying to prevent the tragedy of another school shooting. And believe us, we are not trying to minimize how terrible the tragedy is. But the truth of the matter is, school shootings are extremely rare. Because the federal government does not keep a database of school shootings, the Washington Post has maintained its own running tally. Between 1999 and January 2020 (the date of the most recent school shootings with a death in the US at the time this paragraph was written), the Post reported a total of 254 people died in school shootings in the US. Not 254 per year, 254 total. That is an average of 12 per year. Of course, that is 254 people who should not have died (particularly because many were children), but in a country with approximately 60,000,000 students and teachers, this is a very small risk.
But many students and teachers are terrified that they will be victims of school shootings because of the availability heuristic. It is so easy to think of examples (they are very available to memory) that people believe the event is very common. It is not. And there is a downside to this. We happen to believe that there is an enormous gun violence problem in the United States. According to the Centers for Disease Control and Prevention, there were 39,773 firearm deaths in the US in 2017. Fifteen of those deaths were in school shootings, according to the Post. 60% of those deaths were suicides. When people pay attention to the school shooting risk (low), they often fail to notice the much larger risk.
And examples like this are by no means unique. The authors of this book have been teaching psychology since the 1990s. We have been able to make the exact same arguments about the misapplication of the availability heuristics and keep them current by simply swapping out for the “fear of the day.” In the 1990’s it was children being kidnapped by strangers (it was known as “stranger danger”) despite the facts that kidnappings accounted for only 2% of the violent crimes committed against children, and only 24% of kidnappings are committed by strangers (US Department of Justice, 2007). This fear overlapped with the fear of terrorism that gripped the country after the 2001 terrorist attacks on the World Trade Center and US Pentagon and still plagues the population of the US somewhat in 2020. After a well-publicized, sensational act of violence, people are extremely likely to increase their estimates of the chances that they, too, will be victims of terror. Think about the reality, however. In October of 2001, a terrorist mailed anthrax spores to members of the US government and a number of media companies. A total of five people died as a result of this attack. The nation was nearly paralyzed by the fear of dying from the attack; in reality, the probability of an individual person dying was 0.00000002.
The availability heuristic can lead you to make incorrect judgments in a school setting as well. For example, suppose you are trying to decide if you should take a class from a particular math professor. You might try to make a judgment of how good a teacher she is by recalling instances of friends and acquaintances making comments about her teaching skill. You may have some examples that suggest that she is a poor teacher very available to memory, so on the basis of the availability heuristic, you judge her a poor teacher and decide to take the class from someone else. What if, however, the instances you recalled were all from the same person, and this person happens to be a very colorful storyteller? The subsequent ease of remembering the instances might not indicate that the professor is a poor teacher after all.
Although the availability heuristic is obviously important, it is not the only judgment heuristic we use. Amos Tversky and Daniel Kahneman examined the role of heuristics in inductive reasoning in a long series of studies. Kahneman received a Nobel Prize in Economics for this research in 2002, and Tversky would have certainly received one as well if he had not died of melanoma at age 59 in 1996 (Nobel Prizes are not awarded posthumously). Kahneman and Tversky demonstrated repeatedly that people do not reason in ways that are consistent with the laws of probability. They identified several heuristic strategies that people use instead to make judgments about likelihood. The importance of this work for economics (and the reason that Kahneman was awarded the Nobel Prize) is that earlier economic theories had assumed that people do make judgments rationally, that is, in agreement with the laws of probability.
Another common heuristic that people use for making judgments is the representativeness heuristic (Kahneman & Tversky 1973). Suppose we describe a person to you. He is quiet and shy, has an unassuming personality, and likes to work with numbers. Is this person more likely to be an accountant or an attorney? If you said accountant, you were probably using the representativeness heuristic. Our imaginary person is judged likely to be an accountant because he resembles, or is representative of the concept of, an accountant. When research participants are asked to make judgments such as these, the only thing that seems to matter is the representativeness of the description. For example, if told that the person described is in a room that contains 70 attorneys and 30 accountants, participants will still assume that he is an accountant.
inductive reasoning: a type of reasoning in which we make judgments about likelihood from sets of evidence
inductively strong argument: an inductive argument in which the beginning statements lead to a conclusion that is probably true
heuristic: a shortcut strategy that we use to make judgments and solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions
availability heuristic: judging the frequency or likelihood of some event type according to how easily examples of the event can be called to mind (i.e., how available they are to memory)
representativeness heuristic: judging the likelihood that something is a member of a category on the basis of how much it resembles a typical category member (i.e., how representative it is of the category)
Type 1 thinking: fast, automatic, and emotional thinking.
Type 2 thinking : slow, effortful, and logical thinking.
- What percentage of workplace homicides are co-worker violence?
Many people get these questions wrong. The answers are 10%; stairs; skin; 6%. How close were your answers? Explain how the availability heuristic might have led you to make the incorrect judgments.
- Can you think of some other judgments that you have made (or beliefs that you have) that might have been influenced by the availability heuristic?
7.3 Problem Solving
- Please take a few minutes to list a number of problems that you are facing right now.
- Now write about a problem that you recently solved.
- What is your definition of a problem?
Mary has a problem. Her daughter, ordinarily quite eager to please, appears to delight in being the last person to do anything. Whether getting ready for school, going to piano lessons or karate class, or even going out with her friends, she seems unwilling or unable to get ready on time. Other people have different kinds of problems. For example, many students work at jobs, have numerous family commitments, and are facing a course schedule full of difficult exams, assignments, papers, and speeches. How can they find enough time to devote to their studies and still fulfill their other obligations? Speaking of students and their problems: Show that a ball thrown vertically upward with initial velocity v0 takes twice as much time to return as to reach the highest point (from Spiegel, 1981).
These are three very different situations, but we have called them all problems. What makes them all the same, despite the differences? A psychologist might define a problem as a situation with an initial state, a goal state, and a set of possible intermediate states. Somewhat more meaningfully, we might consider a problem a situation in which you are in here one state (e.g., daughter is always late), you want to be there in another state (e.g., daughter is not always late), and with no obvious way to get from here to there. Defined this way, each of the three situations we outlined can now be seen as an example of the same general concept, a problem. At this point, you might begin to wonder what is not a problem, given such a general definition. It seems that nearly every non-routine task we engage in could qualify as a problem. As long as you realize that problems are not necessarily bad (it can be quite fun and satisfying to rise to the challenge and solve a problem), this may be a useful way to think about it.
Can we identify a set of problem-solving skills that would apply to these very different kinds of situations? That task, in a nutshell, is a major goal of this section. Let us try to begin to make sense of the wide variety of ways that problems can be solved with an important observation: the process of solving problems can be divided into two key parts. First, people have to notice, comprehend, and represent the problem properly in their minds (called problem representation ). Second, they have to apply some kind of solution strategy to the problem. Psychologists have studied both of these key parts of the process in detail.
When you first think about the problem-solving process, you might guess that most of our difficulties would occur because we are failing in the second step, the application of strategies. Although this can be a significant difficulty much of the time, the more important source of difficulty is probably problem representation. In short, we often fail to solve a problem because we are looking at it, or thinking about it, the wrong way.
problem: a situation in which we are in an initial state, have a desired goal state, and there is a number of possible intermediate states (i.e., there is no obvious way to get from the initial to the goal state)
problem representation: noticing, comprehending and forming a mental conception of a problem
Defining and Mentally Representing Problems in Order to Solve Them
So, the main obstacle to solving a problem is that we do not clearly understand exactly what the problem is. Recall the problem with Mary’s daughter always being late. One way to represent, or to think about, this problem is that she is being defiant. She refuses to get ready in time. This type of representation or definition suggests a particular type of solution. Another way to think about the problem, however, is to consider the possibility that she is simply being sidetracked by interesting diversions. This different conception of what the problem is (i.e., different representation) suggests a very different solution strategy. For example, if Mary defines the problem as defiance, she may be tempted to solve the problem using some kind of coercive tactics, that is, to assert her authority as her mother and force her to listen. On the other hand, if Mary defines the problem as distraction, she may try to solve it by simply removing the distracting objects.
As you might guess, when a problem is represented one way, the solution may seem very difficult, or even impossible. Seen another way, the solution might be very easy. For example, consider the following problem (from Nasar, 1998):
Two bicyclists start 20 miles apart and head toward each other, each going at a steady rate of 10 miles per hour. At the same time, a fly that travels at a steady 15 miles per hour starts from the front wheel of the southbound bicycle and flies to the front wheel of the northbound one, then turns around and flies to the front wheel of the southbound one again, and continues in this manner until he is crushed between the two front wheels. Question: what total distance did the fly cover?
Please take a few minutes to try to solve this problem.
Most people represent this problem as a question about a fly because, well, that is how the question is asked. The solution, using this representation, is to figure out how far the fly travels on the first leg of its journey, then add this total to how far it travels on the second leg of its journey (when it turns around and returns to the first bicycle), then continue to add the smaller distance from each leg of the journey until you converge on the correct answer. You would have to be quite skilled at math to solve this problem, and you would probably need some time and a pencil and paper to do it.
If you consider a different representation, however, you can solve this problem in your head. Instead of thinking about it as a question about a fly, think about it as a question about the bicycles. They are 20 miles apart, and each is traveling 10 miles per hour. How long will it take for the bicycles to reach each other? Right, one hour. The fly is traveling 15 miles per hour; therefore, it will travel a total of 15 miles back and forth in the hour before the bicycles meet. Represented one way (as a problem about a fly), the problem is quite difficult. Represented another way (as a problem about two bicycles), it is easy. Changing your representation of a problem is sometimes the best—sometimes the only—way to solve it.
Unfortunately, however, changing a problem’s representation is not the easiest thing in the world to do. Often, problem solvers get stuck looking at a problem one way. This is called fixation . Most people who represent the preceding problem as a problem about a fly probably do not pause to reconsider, and consequently change, their representation. A parent who thinks her daughter is being defiant is unlikely to consider the possibility that her behavior is far less purposeful.
Problem-solving fixation was examined by a group of German psychologists called Gestalt psychologists during the 1930s and 1940s. Karl Dunker, for example, discovered an important type of failure to take a different perspective called functional fixedness . Imagine being a participant in one of his experiments. You are asked to figure out how to mount two candles on a door and are given an assortment of odds and ends, including a small empty cardboard box and some thumbtacks. Perhaps you have already figured out a solution: tack the box to the door so it forms a platform, then put the candles on top of the box. Most people are able to arrive at this solution. Imagine a slight variation of the procedure, however. What if, instead of being empty, the box had matches in it? Most people given this version of the problem do not arrive at the solution given above. Why? Because it seems to people that when the box contains matches, it already has a function; it is a matchbox. People are unlikely to consider a new function for an object that already has a function. This is functional fixedness.
Mental set is a type of fixation in which the problem solver gets stuck using the same solution strategy that has been successful in the past, even though the solution may no longer be useful. It is commonly seen when students do math problems for homework. Often, several problems in a row require the reapplication of the same solution strategy. Then, without warning, the next problem in the set requires a new strategy. Many students attempt to apply the formerly successful strategy on the new problem and therefore cannot come up with a correct answer.
The thing to remember is that you cannot solve a problem unless you correctly identify what it is to begin with (initial state) and what you want the end result to be (goal state). That may mean looking at the problem from a different angle and representing it in a new way. The correct representation does not guarantee a successful solution, but it certainly puts you on the right track.
A bit more optimistically, the Gestalt psychologists discovered what may be considered the opposite of fixation, namely insight . Sometimes the solution to a problem just seems to pop into your head. Wolfgang Kohler examined insight by posing many different problems to chimpanzees, principally problems pertaining to their acquisition of out-of-reach food. In one version, a banana was placed outside of a chimpanzee’s cage and a short stick inside the cage. The stick was too short to retrieve the banana but was long enough to retrieve a longer stick also located outside of the cage. This second stick was long enough to retrieve the banana. After trying, and failing, to reach the banana with the shorter stick, the chimpanzee would try a couple of random-seeming attempts, react with some apparent frustration or anger, then suddenly rush to the longer stick, the correct solution fully realized at this point. This sudden appearance of the solution, observed many times with many different problems, was termed insight by Kohler.
Lest you think it pertains to chimpanzees only, Karl Dunker demonstrated that children also solve problems through insight in the 1930s. More importantly, you have probably experienced insight yourself. Think back to a time when you were trying to solve a difficult problem. After struggling for a while, you gave up. Hours later, the solution just popped into your head, perhaps when you were taking a walk, eating dinner, or lying in bed.
fixation: when a problem solver gets stuck looking at a problem a particular way and cannot change their representation of it (or their intended solution strategy)
functional fixedness: a specific type of fixation in which a problem solver cannot think of a new use for an object that already has a function
mental set: a specific type of fixation in which a problem solver gets stuck using the same solution strategy that has been successful in the past
insight: a sudden realization of a solution to a problem
Solving Problems by Trial and Error
Correctly identifying the problem and your goal for a solution is a good start, but recall the psychologist’s definition of a problem: it includes a set of possible intermediate states. Viewed this way, a problem can be solved satisfactorily only if one can find a path through some of these intermediate states to the goal. Imagine a fairly routine problem, finding a new route to school when your ordinary route is blocked (by road construction, for example). At each intersection, you may turn left, turn right, or go straight. A satisfactory solution to the problem (of getting to school) is a sequence of selections at each intersection that allows you to wind up at school.
If you had all the time in the world to get to school, you might try choosing intermediate states randomly. At one corner you turn left, the next you go straight, then you go left again, then right, then right, then straight. Unfortunately, trial and error will not necessarily get you where you want to go, and even if it does, it is not the fastest way to get there. For example, when a friend of ours was in college, he got lost on the way to a concert and attempted to find the venue by choosing streets to turn onto randomly (this was long before the use of GPS). Amazingly enough, the strategy worked, although he did end up missing two out of the three bands who played that night.
Trial and error is not all bad, however. B.F. Skinner, a prominent behaviorist psychologist, suggested that people often behave randomly in order to see what effect the behavior has on the environment and what subsequent effect this environmental change has on them. This seems particularly true for the very young person. Picture a child filling a household’s fish tank with toilet paper, for example. To a child trying to develop a repertoire of creative problem-solving strategies, an odd and random behavior might be just the ticket. Eventually, the exasperated parent hopes, the child will discover that many of these random behaviors do not successfully solve problems; in fact, in many cases they create problems. Thus, one would expect a decrease in this random behavior as a child matures. You should realize, however, that the opposite extreme is equally counterproductive. If the children become too rigid, never trying something unexpected and new, their problem-solving skills can become too limited.
Effective problem solving seems to call for a happy medium that strikes a balance between using well-founded old strategies and trying new ground and territory. The individual who recognizes a situation in which an old problem-solving strategy would work best, and who can also recognize a situation in which a new untested strategy is necessary is halfway to success.
Solving Problems with Algorithms and Heuristics
For many problems there is a possible strategy available that will guarantee a correct solution. For example, think about math problems. Math lessons often consist of step-by-step procedures that can be used to solve the problems. If you apply the strategy without error, you are guaranteed to arrive at the correct solution to the problem. This approach is called using an algorithm , a term that denotes the step-by-step procedure that guarantees a correct solution. Because algorithms are sometimes available and come with a guarantee, you might think that most people use them frequently. Unfortunately, however, they do not. As the experience of many students who have struggled through math classes can attest, algorithms can be extremely difficult to use, even when the problem solver knows which algorithm is supposed to work in solving the problem. In problems outside of math class, we often do not even know if an algorithm is available. It is probably fair to say, then, that algorithms are rarely used when people try to solve problems.
Because algorithms are so difficult to use, people often pass up the opportunity to guarantee a correct solution in favor of a strategy that is much easier to use and yields a reasonable chance of coming up with a correct solution. These strategies are called problem solving heuristics . Similar to what you saw in section 6.2 with reasoning heuristics, a problem-solving heuristic is a shortcut strategy that people use when trying to solve problems. It usually works pretty well, but does not guarantee a correct solution to the problem. For example, one problem-solving heuristic might be “always move toward the goal” (so when trying to get to school when your regular route is blocked, you would always turn in the direction you think the school is). A heuristic that people might use when doing math homework is “use the same solution strategy that you just used for the previous problem.”
By the way, we hope these last two paragraphs feel familiar to you. They seem to parallel a distinction that you recently learned. Indeed, algorithms and problem-solving heuristics are another example of the distinction between Type 1 thinking and Type 2 thinking.
Although it is probably not worth describing a large number of specific heuristics, two observations about heuristics are worth mentioning. First, heuristics can be very general or they can be very specific, pertaining to a particular type of problem only. For example, “always move toward the goal” is a general strategy that you can apply to countless problem situations. On the other hand, “when you are lost without a functioning GPS, pick the most expensive car you can see and follow it” is specific to the problem of being lost. Second, all heuristics are not equally useful. One heuristic that many students know is “when in doubt, choose c for a question on a multiple-choice exam.” This is a dreadful strategy because many instructors intentionally randomize the order of answer choices. Another test-taking heuristic, somewhat more useful, is “look for the answer to one question somewhere else on the exam.”
You really should pay attention to the application of heuristics to test-taking. Imagine that while reviewing your answers for a multiple-choice exam before turning it in, you come across a question for which you originally thought the answer was c. Upon reflection, you now think that the answer might be b. Should you change the answer to b, or should you stick with your first impression? Most people will apply the heuristic strategy to “stick with your first impression.” What they do not realize, of course, is that this is a very poor strategy (Lilienfeld et al., 2009). Most of the errors on exams come on questions that were answered wrong originally and were not changed (so they remain wrong). There are many fewer errors where we change a correct answer to an incorrect answer. And, of course, sometimes we change an incorrect answer to a correct answer. In fact, research has shown that it is more common to change a wrong answer to a right answer than vice versa (Bruno, 2001).
The belief in this poor test-taking strategy (stick with your first impression) is based on the confirmation bias (Nickerson, 1998; Wason, 1960). You first saw the confirmation bias in Module 1, but because it is so important, we will repeat the information here. People have a bias, or tendency, to notice information that confirms what they already believe. Somebody at one time told you to stick with your first impression, so when you look at the results of an exam you have taken, you will tend to notice the cases that are consistent with that belief. That is, you will notice the cases in which you originally had an answer correct and changed it to the wrong answer. You tend not to notice the other two important (and more common) cases, changing an answer from wrong to right, and leaving a wrong answer unchanged.
Because heuristics by definition do not guarantee a correct solution to a problem, mistakes are bound to occur when we employ them. A poor choice of a specific heuristic will lead to an even higher likelihood of making an error.
algorithm: a step-by-step procedure that guarantees a correct solution to a problem
problem solving heuristic: a shortcut strategy that we use to solve problems. Although they are easy to use, they do not guarantee correct judgments and solutions
confirmation bias: people’s tendency to notice information that confirms what they already believe
An Effective Problem-Solving Sequence
You may be left with a big question: If algorithms are hard to use and heuristics often don’t work, how am I supposed to solve problems? Robert Sternberg (1996), as part of his theory of what makes people successfully intelligent (Module 8) described a problem-solving sequence that has been shown to work rather well:
- Identify the existence of a problem. In school, problem identification is often easy; problems that you encounter in math classes, for example, are conveniently labeled as problems for you. Outside of school, however, realizing that you have a problem is a key difficulty that you must get past in order to begin solving it. You must be very sensitive to the symptoms that indicate a problem.
- Define the problem. Suppose you realize that you have been having many headaches recently. Very likely, you would identify this as a problem. If you define the problem as “headaches,” the solution would probably be to take aspirin or ibuprofen or some other anti-inflammatory medication. If the headaches keep returning, however, you have not really solved the problem—likely because you have mistaken a symptom for the problem itself. Instead, you must find the root cause of the headaches. Stress might be the real problem. For you to successfully solve many problems it may be necessary for you to overcome your fixations and represent the problems differently. One specific strategy that you might find useful is to try to define the problem from someone else’s perspective. How would your parents, spouse, significant other, doctor, etc. define the problem? Somewhere in these different perspectives may lurk the key definition that will allow you to find an easier and permanent solution.
- Formulate strategy. Now it is time to begin planning exactly how the problem will be solved. Is there an algorithm or heuristic available for you to use? Remember, heuristics by their very nature guarantee that occasionally you will not be able to solve the problem. One point to keep in mind is that you should look for long-range solutions, which are more likely to address the root cause of a problem than short-range solutions.
- Represent and organize information. Similar to the way that the problem itself can be defined, or represented in multiple ways, information within the problem is open to different interpretations. Suppose you are studying for a big exam. You have chapters from a textbook and from a supplemental reader, along with lecture notes that all need to be studied. How should you (represent and) organize these materials? Should you separate them by type of material (text versus reader versus lecture notes), or should you separate them by topic? To solve problems effectively, you must learn to find the most useful representation and organization of information.
- Allocate resources. This is perhaps the simplest principle of the problem-solving sequence, but it is extremely difficult for many people. First, you must decide whether time, money, skills, effort, goodwill or some other resource would help to solve the problem Then, you must make the hard choice of deciding which resources to use, realizing that you cannot devote maximum resources to every problem. Very often, the solution to the problem is simply to change how resources are allocated (for example, spending more time studying in order to improve grades).
- Monitor and evaluate solutions. Pay attention to the solution strategy while you are applying it. If it is not working, you may be able to select another strategy. Another fact you should realize about problem-solving is that it never does end. Solving one problem frequently brings up new ones. Good monitoring and evaluation of your problem solutions can help you to anticipate and get a jump on solving the inevitable new problems that will arise.
Please note that this is an effective problem-solving sequence, not THE effective problem-solving sequence. Just as you can become fixated and end up representing the problem incorrectly or trying an inefficient solution, you can become stuck applying the problem-solving sequence in an inflexible way. Clearly, there are problem situations that can be solved without using these skills in this order.
Additionally, many real-world problems may require that you go back and redefine a problem several times as the situation changes (Sternberg et al., 2000). For example, consider the problem with Mary’s daughter one last time. At first, Mary did represent the problem as one of defiance. When her early strategy of pleading and threatening punishment was unsuccessful, Mary began to observe her daughter more carefully. She noticed that, indeed, her daughter’s attention would be drawn by an irresistible distraction or book. Fresh with a re-representation of the problem, she began a new solution strategy. She began to remind her daughter every few minutes to stay on task and remind her that if she is ready before it is time to leave, she may return to the book or other distracting object at that time. Fortunately, this strategy was successful, so Mary did not have to go back and redefine the problem again.
Pick one or two of the problems that you listed when you first started studying this section and try to work out the steps of Sternberg’s problem-solving sequence for each one.
Introduction to Psychology, 2nd Edition Copyright © 2021 by Ken Gray; Elizabeth Arnott-Hill; and Or'Shaundra Benson is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License , except where otherwise noted.
Share This Book
7.5 Problem-Solving
| Estimated completion time: 12 minutes. |
Questions to Consider:
- How can determining the best approach to solve a problem help you generate solutions?
- Why do thinkers create multiple solutions to problems?
When we’re solving a problem, whether at work, school, or home, we are being asked to perform multiple, often complex, tasks. The most effective problem-solving approach includes some variation of the following steps:
- Determine the issue(s)
- Recognize other perspectives
- Think of multiple possible results
- Research and evaluate the possibilities
- Select the best result(s)
- Communicate your findings
- Establish logical action items based on your analysis
Determining the best approach to any given problem and generating more than one possible solution to the problem constitutes the complicated process of problem-solving. People who are good at these skills are highly marketable because many jobs consist of a series of problems that need to be solved for production, services, goods, and sales to continue smoothly. Think about what happens when a worker at your favorite coffee shop slips on a wet spot behind the counter, dropping several drinks she just prepared. One problem is the employee may be hurt, in need of attention, and probably embarrassed; another problem is that several customers do not have the drinks they were waiting for; and another problem is that stopping production of drinks (to care for the hurt worker, to clean up her spilled drinks, to make new drinks) causes the line at the cash register to back up. A good manager has to juggle all of these elements to resolve the situation as quickly and efficiently as possible. That resolution and return to standard operations doesn’t happen without a great deal of thinking: prioritizing needs, shifting other workers off one station onto another temporarily, and dealing with all the people involved, from the injured worker to the impatient patrons.
Determining the Best Approach
Faced with a problem-solving opportunity, you must assess the skills you will need to create solutions. Problem-solving can involve many different types of thinking. You may have to call on your creative, analytical, or critical thinking skills—or more frequently, a combination of several different types of thinking—to solve a problem satisfactorily. When you approach a situation, how can you decide what is the best type of thinking to employ? Sometimes the answer is obvious; if you are working a scientific challenge, you likely will use analytical thinking; if you are a design student considering the atmosphere of a home, you may need to tap into creative thinking skills; and if you are an early childhood education major outlining the logistics involved in establishing a summer day camp for children, you may need a combination of critical, analytical, and creative thinking to solve this challenge.
What sort of thinking do you imagine initially helped in the following scenarios? How would the other types of thinking come into resolving these problems?
- Analytical thinking
- Creative thinking
- Critical thinking
Write a one- to two-sentence rationale for why you chose the answers you did on the above survey.
Generating Multiple Solutions
Why do you think it is important to provide multiple solutions when you’re going through the steps to solve problems? Typically, you’ll end up only using one solution at a time, so why expend the extra energy to create alternatives? If you planned a wonderful trip to Europe and had all the sites you want to see planned out and reservations made, you would think that your problem-solving and organizational skills had quite a workout. But what if when you arrived, the country you’re visiting is enmeshed in a public transportation strike experts predict will last several weeks if not longer? A back-up plan would have helped you contemplate alternatives you could substitute for the original plans. You certainly cannot predict every possible contingency—sick children, weather delays, economic downfalls—but you can be prepared for unexpected issues to come up and adapt more easily if you plan for multiple solutions.
Write out at least two possible solutions to these dilemmas:
- Your significant other wants a birthday present—you have no cash.
- You have three exams scheduled on a day when you also need to work.
- Your car needs new tires, an oil change, and gas—you have no cash. (Is there a trend here?)
- You have to pass a running test for your physical education class, but you’re out of shape.
Providing more than one solution to a problem gives people options. You may not need several options, but having more than one solution will allow you to feel more in control and part of the problem-solving process.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/college-success/pages/1-introduction
- Authors: Amy Baldwin
- Publisher/website: OpenStax
- Book title: College Success
- Publication date: Mar 27, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/college-success/pages/1-introduction
- Section URL: https://openstax.org/books/college-success/pages/7-5-problem-solving
© Sep 20, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Math Expressions Grade 3 Unit 7 Lesson 8 Answer Key Problem Solving with Fractions
Solve the questions in Math Expressions Grade 3 Homework and Remembering Answer Key Unit 7 Lesson 8 Answer Key Problem Solving with Fractions to attempt the exam with higher confidence. https://mathexpressionsanswerkey.com/math-expressions-grade-3-unit-7-lesson-8-answer-key/
Math Expressions Common Core Grade 3 Unit 7 Lesson 8 Answer Key Problem Solving with Fractions
Math Expressions Grade 3 Unit 7 Lesson 8 Homework
Solve. Draw diagrams or number lines if it helps.
Unit 7 Lesson 8 Math Expressions Grade 3 Answer Key Question 1. Jack buys \(\frac{4}{3}\) pounds of plums. Martin buys \(\frac{6}{3}\) pounds of apples. Who buys more fruit? Explain your answer. Answer: Martin has more fruits.
Explanation: Given that Jack buys \(\frac{4}{3}\) pounds of plums and Martin buys \(\frac{6}{3}\) pounds of apples. So who bought more fruit is Martin, as Martin has more apples which are 2 pounds and Jack has 1.3 pounds. So Martin has more fruits.
Unit 5 Lesson 10 Answer Key Grade 3 Problem Solving with Fractions Question 2. May runs \(\frac{10}{4}\) miles every day after school. Beth says that she runs farther than May every day because she runs \(\frac{5}{2}\) miles every day after school. Is her statement correct? Explain your answer. Answer: Beth’s statement is not correct.
Explanation: Given that May runs \(\frac{10}{4}\) miles every day after school. Beth says that she runs farther than May every day because she runs \(\frac{5}{2}\) miles every day after school. Here, Beth’s statement is not correct. As \(\frac{10}{4}\) is equivalent fraction of \(\frac{5}{2}\), they both ran same number of miles.
Lesson 8 Answer Key Grade 3 Math Expressions Unit 7 Question 3. Bess has knitted \(\frac{5}{8}\) of the scarf she is making. Has she knitted more than \(\frac{1}{2}\) of the scarf? Hint. Find an equivalent fraction in eighths for \(\frac{1}{2}\). Answer: Yes, Bess knitted more than \(\frac{1}{2}\) and the equivalent fraction in eighths for \(\frac{1}{2}\) is \(\frac{4}{8}\).
Explanation: Given that Bess has knitted \(\frac{5}{8}\) of the scarf she is making. Yes, she knitted more than \(\frac{1}{2}\) of the scarf as \(\frac{5}{8}\) is greater than \(\frac{1}{2}\). The equivalent fraction in eighths for \(\frac{1}{2}\) is \(\frac{4}{8}\).
Unit 7 Lesson 8 Problem Solving with Fractions Question 4. Bert used \(\frac{7}{8}\) foot of an oak board to make a tray. Akio made his tray from \(\frac{4}{4}\) foot of the same oak board. Who used more wood? How do you know? Answer: Akio used more feet of the oak board.
Explanation: Given that Bert used \(\frac{7}{8}\) foot of an oak board to make a tray and Akio made his tray from \(\frac{4}{4}\) foot of the same oak board. Here, Akio used more feet of the oak board as \(\frac{4}{4}\) is greater than \(\frac{7}{8}\).
Math Expressions Lesson 8 Solving with Fractions Grade 3 Unit 7 Question 5. A bottle of orange juice holds \(\frac{4}{6}\) quart of juice. A bottle of pineapple juice holds \(\frac{2}{3}\) quart of juice. Which bottle has more juice? How do you know? Answer: Both the bottles have the same quarts of juice.
Explanation: Given that a bottle of orange juice holds \(\frac{4}{6}\) quart of juice and a bottle of pineapple juice holds \(\frac{2}{3}\) quart of juice. Here, both the bottles have the same quarts of juice, as \(\frac{4}{6}\) is equal to \(\frac{2}{3}\).
Math Expressions Grade 3 Unit 7 Lesson 8 Remembering
The table shows the number of each type of book sold on Monday and Tuesday at the book sale.

Problem Solving with Fractions Grade 3 Unit 7 Answer Key Lesson 8 Question 1. On Monday, how many more nonfiction and used books are sold than fiction books? Answer: The number of nonfiction and used books are sold than fiction books is 35 books.
Explanation: On Monday, the total number of nonfiction and used books are 166+92 = 258, and the fiction books are 223. So the number of nonfiction and used books are sold than fiction books is 258 – 223 = 35 books.
Question 2. How many books were sold on Tuesday? Answer: The number of books that are sold on Tuesday is 482 books.
Explanation: The number of books that are sold on Tuesday is 137 + 257 + 88= 482 books.
Solve. Draw a diagram to represent the situation.

Complete the number line. Show all fractions including the fraction for 1.

Question 5. Stretch Your Thinking Christine and Alan each buy the same size sandwich. Christine eats \(\frac{3}{4}\) of her sandwich. Alan eats more of his sandwich than Christine. Use a different denominator to show how much of the sandwich Alan might have eaten. Answer: Alan eats \(\frac{6}{8}\) of her sandwich.
Explanation: Given that Christine eats \(\frac{3}{4}\) of her sandwich and Alan eats more of his sandwich than Christine. So Alan eats \(\frac{6}{8}\) of her sandwich.
Leave a Comment Cancel reply
Save my name, email, and website in this browser for the next time I comment.

Thinking and Intelligence
Introduction to Thinking and Problem-Solving
What you’ll learn to do: describe cognition and problem-solving strategies.

Imagine all of your thoughts as if they were physical entities, swirling rapidly inside your mind. How is it possible that the brain is able to move from one thought to the next in an organized, orderly fashion? The brain is endlessly perceiving, processing, planning, organizing, and remembering—it is always active. Yet, you don’t notice most of your brain’s activity as you move throughout your daily routine. This is only one facet of the complex processes involved in cognition. Simply put, cognition is thinking, and it encompasses the processes associated with perception, knowledge, problem solving, judgment, language, and memory. Scientists who study cognition are searching for ways to understand how we integrate, organize, and utilize our conscious cognitive experiences without being aware of all of the unconscious work that our brains are doing (for example, Kahneman, 2011).
Learning Objectives
- Distinguish between concepts and prototypes
- Explain the difference between natural and artificial concepts
- Describe problem solving strategies, including algorithms and heuristics
- Explain some common roadblocks to effective problem solving
CC licensed content, Original
- Modification, adaptation, and original content. Provided by : Lumen Learning. License : CC BY: Attribution
CC licensed content, Shared previously
- What Is Cognition?. Authored by : OpenStax College. Located at : https://openstax.org/books/psychology-2e/pages/7-1-what-is-cognition . License : CC BY: Attribution . License Terms : Download for free at https://openstax.org/books/psychology-2e/pages/1-introduction
- A Thinking Man Image. Authored by : Wesley Nitsckie. Located at : https://www.flickr.com/photos/nitsckie/5507777269 . License : CC BY-SA: Attribution-ShareAlike
General Psychology Copyright © by OpenStax and Lumen Learning is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
Share This Book

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Unit 2: Creativity and Language Learning

Activity 3: Problem Solving
Part a: group discussion, group discussion.
Work in groups and discuss your answers to the following questions.
Part B: Read the Article
Read the article.
Skim the text below and find the benefits of using creativity in problem solving.
How to become a creative problem solver
by Louise Cunnah posted in Quick Tips
Problem solving and creative thinking; these are two great skills to possess in various areas of your life, from education to the workplace, and ones that work in perfect harmony with each other. No matter the task at hand, becoming a creative problem solver is something we should all strive to achieve as it can help to give us fresh perspectives when troubleshooting problems that, at first glance, appear to be unsolvable.
Though ‘creativity’ is a quality that’s most commonly associated with art, design and writing, it is a highly flexible skill that can be applied to countless tasks – making it one of the most important to have under our belts. In fact, when it comes to solving problems, creative thinking becomes incredibly useful. This is because not every problem is the same, and they can’t all be solved in the same way. By utilizing creativity in problem solving, you can devise innovative solutions that might be just the ticket, but others haven’t thought to try.
Additionally, if you can’t crack the riddle with conventional methods, Creative Problem Solving (CPS) will stop you from giving up at the first hurdle. This makes you far more likely to achieve your personal and business goals.
But don’t worry if you don’t consider yourself to be a creative thinker; everyone has the power to be creative. It’s all about knowing the right tools and techniques to help get you there. So, what exactly is a Creative Problem Solver and how can you become one?
What is Creative Problem Solving?
Creative Problem Solving is a term that has been around for many years, initially being coined by Alex Faikney Osbourne in the 1940s (who is also responsible for popularizing ‘ brainstorming ’). It was developed with the help of Sid Parnes in the 1950s, becoming the Osborn-Parnes Creative Problem Solving process called the CPS Learner’s Model.
According to the Creative Education Foundation (which was founded by Osbourne), CPS begins with the assumption that everyone is creative in some way, and that creativity can be learned or developed further. The CPS Model outlines that the process of Creative Problem Solving should incorporate the following steps:
- Clarify: Identify the goal, gather data to understand the challenges you may encounter when achieving this goal, and create “challenge questions” that invite solutions (such as “is there enough time to complete the necessary actions?”).
- Ideate: Generate ideas that answer the challenge questions you identified.
- Develop: Turn your ideas into solutions by evaluating and strengthening them. You can then choose the solutions that best “fit” the goal and its challenges.
- Implement: Formulate a plan by identifying resources and actions that will support the implementation of your selected solutions.
Although Creative Problem Solving isn’t new, many businesses and organizations are now realizing the importance of creativity in problem solving. As Adobe has pointed out , the US Department of Education, World Economic Forum, and Bloomberg have all indicated that the jobs of the future will require creative problem-solving skills. In addition to this, 90% of surveyed educators said that it should be implemented across all curricula in education.
With all that in mind, here are just some of the techniques you can utilize to become a creative problem solver:
Mind Mapping
Mind Maps, by their very nature, are creative. Though they’re also an effective tool for boosting memory and recall due to their visual nature (often incorporating a range of shapes, colors and imagery), their flowing layout and use of keywords and short phrases also encourage our brains to make associations between ideas, thus enabling us to think more creatively.
With this in mind, it shouldn’t be surprising that Mind Mapping also lends itself to being a great problem-solving technique. Solving a problem can be stressful and overwhelming when you first attempt to tackle it, which can make it harder to generate potential solutions. Fortunately, using Mind Maps in your problem solving can help you to organize your thoughts, as well as stimulate your brain to devise more creative ideas – which is essential for every stage of the CPS Model.
The Six Thinking Hats
This problem-solving technique requires you to move beyond your comfort zone and consider a problem from a range of different perspectives by essentially wearing different thinking hats. Humans are creatures of habit; if someone is an emotional thinker, they will have a tendency to approach every problem with this mindset, resulting in similar conclusions being drawn each time. Whether you use the Six Thinking Hats technique on your own or in a group, it forces you to get a more rounded view of the problem at hand, resulting in more creative problem solving.
Each of the six hats is a different color to signify a different way of thinking. When someone is wearing the White Hat, for example, they need to focus on the available facts and figures, using this to analyze past trends and fill in gaps in their knowledge. When they switch to the Red Hat, they need to consider how people will react emotionally. Wearers of The Blue Hat will focus on the decision’s possible negative outcomes, while wearers of the Yellow Hat are more optimistic. When wearing the Green Hat, this is the time to use tools such as Mind Mapping to brainstorm and generate more creative solutions. Finally, the wearer of the Blue Hat is the person that sets objectives, defines the problem, and draws conclusions from the meeting; think of them as ‘the chairman’, if you will.
Focused daydreaming
We all know that we don’t get our best ideas when we’re sitting at a desk, having stared at the same notebook for the past 20 minutes while willing ourselves to think of something, anything creative to jot down. Instead, inspiration tends to strike later, and when we least expect it. More often or not, this happens when we’re daydreaming while we’re doing something else – such as listening to music on the train home from work or relaxing in the bath.
But before you put your computer into sleep mode and head off for a walk, it’s important to know that daydreaming is most beneficial when it’s focused – especially when it comes to solving a specific problem. So, before you chuck your coat on, make sure you gather as much information as you can about the problem beforehand, so you can generate as many creative solutions as possible (after all, knowledge is power), and define what exactly it is that you want to achieve. Then you can let your wandering mind do the creative thinking.
Reversing the problem
One thing that sets Creative Problem Solvers apart from others is their ability to utilize different techniques to tackle a problem from various angles. Turning a problem on its head by looking at it in reverse can be highly useful (whether this is done alone or with a group). It encourages you to discover new issues that you may not have considered when using conventional brainstorming methods, resulting in more innovative solutions being generated.
So, how do you conduct Reverse Brainstorming correctly? It’s really as simple as it sounds. Take a challenge, such as “how do we acquire more customers?” and flip it so that it becomes “how do we lose customers?”. This is something that you may never have considered before, which can help you be more innovative in your thinking. By looking at a problem from various angles, you can ensure all bases are covered.
Incubating ideas
As we’ve already explained, our best sparks of inspiration come to us when our minds wander; often when we’re waiting for the kettle or boil or having our morning shower. Another way you can take advantage of the creative powers of our wandering, distracted mind is by taking regular breaks, thus allowing our ideas time to ‘incubate’ and develop further.
Like with most tasks, if we force ourselves to keep working without a break, we will eventually ‘burn out’ and fail to be productive. However, research into incubating ideas has found that the best way to utilize breaks to generate creative ideas and innovative solutions to problems is by doing another task that doesn’t require a lot of concentration – for example, going for a walk or doing the dishes. So, spend some time problem solving, take that incubation break, then come back to the problem with that fresh burst of inspiration you needed.
Part C: Definitions
Definitions, part d: read for details.
Read the article from Part B again and answer the following questions in your group.
Each question has a sample answer that will be revealed when you click/tap on the Check button and then Show Solution .
Part E: Critical Thinking
Critical thinking.

To brainstorm solutions, use the following techniques:
Step 1- Divergent Thinking
When producing ideas:
- Strive for quantity (i.e., generate as many ideas as possible)
- Defer judgement (do not evaluate their effectiveness at this point)
- Build off others’ ideas
- Freewheel (at this stage, it is okay to produce wild ideas!)
Step 2- Convergent Thinking

Evaluating the effectiveness of your ideas:
- Rate your ideas
- Cluster your ideas (i.e., put them into different categories)
- Tag your favourites
In your groups, discuss the following questions using the Divergent and Convergent Thinking methods.
For your convenience, you can download an MS Word version of the activities to work on your device or print and fill by hand.
Download Activity Template
Share This Book
- Campus Life
- ...a student.
- ...a veteran.
- ...an alum.
- ...a parent.
- ...faculty or staff.
- UTC Learn (Canvas)
- Class Schedule
- Crisis Resources
- People Finder
- Change Password
UTC RAVE Alert
Critical thinking and problem-solving, jump to: , what is critical thinking, characteristics of critical thinking, why teach critical thinking.
- Teaching Strategies to Help Promote Critical Thinking Skills
References and Resources
When examining the vast literature on critical thinking, various definitions of critical thinking emerge. Here are some samples:
- "Critical thinking is the intellectually disciplined process of actively and skillfully conceptualizing, applying, analyzing, synthesizing, and/or evaluating information gathered from, or generated by, observation, experience, reflection, reasoning, or communication, as a guide to belief and action" (Scriven, 1996).
- "Most formal definitions characterize critical thinking as the intentional application of rational, higher order thinking skills, such as analysis, synthesis, problem recognition and problem solving, inference, and evaluation" (Angelo, 1995, p. 6).
- "Critical thinking is thinking that assesses itself" (Center for Critical Thinking, 1996b).
- "Critical thinking is the ability to think about one's thinking in such a way as 1. To recognize its strengths and weaknesses and, as a result, 2. To recast the thinking in improved form" (Center for Critical Thinking, 1996c).
Perhaps the simplest definition is offered by Beyer (1995) : "Critical thinking... means making reasoned judgments" (p. 8). Basically, Beyer sees critical thinking as using criteria to judge the quality of something, from cooking to a conclusion of a research paper. In essence, critical thinking is a disciplined manner of thought that a person uses to assess the validity of something (statements, news stories, arguments, research, etc.).
Back
Wade (1995) identifies eight characteristics of critical thinking. Critical thinking involves asking questions, defining a problem, examining evidence, analyzing assumptions and biases, avoiding emotional reasoning, avoiding oversimplification, considering other interpretations, and tolerating ambiguity. Dealing with ambiguity is also seen by Strohm & Baukus (1995) as an essential part of critical thinking, "Ambiguity and doubt serve a critical-thinking function and are a necessary and even a productive part of the process" (p. 56).
Another characteristic of critical thinking identified by many sources is metacognition. Metacognition is thinking about one's own thinking. More specifically, "metacognition is being aware of one's thinking as one performs specific tasks and then using this awareness to control what one is doing" (Jones & Ratcliff, 1993, p. 10 ).
In the book, Critical Thinking, Beyer elaborately explains what he sees as essential aspects of critical thinking. These are:
- Dispositions: Critical thinkers are skeptical, open-minded, value fair-mindedness, respect evidence and reasoning, respect clarity and precision, look at different points of view, and will change positions when reason leads them to do so.
- Criteria: To think critically, must apply criteria. Need to have conditions that must be met for something to be judged as believable. Although the argument can be made that each subject area has different criteria, some standards apply to all subjects. "... an assertion must... be based on relevant, accurate facts; based on credible sources; precise; unbiased; free from logical fallacies; logically consistent; and strongly reasoned" (p. 12).
- Argument: Is a statement or proposition with supporting evidence. Critical thinking involves identifying, evaluating, and constructing arguments.
- Reasoning: The ability to infer a conclusion from one or multiple premises. To do so requires examining logical relationships among statements or data.
- Point of View: The way one views the world, which shapes one's construction of meaning. In a search for understanding, critical thinkers view phenomena from many different points of view.
- Procedures for Applying Criteria: Other types of thinking use a general procedure. Critical thinking makes use of many procedures. These procedures include asking questions, making judgments, and identifying assumptions.
Oliver & Utermohlen (1995) see students as too often being passive receptors of information. Through technology, the amount of information available today is massive. This information explosion is likely to continue in the future. Students need a guide to weed through the information and not just passively accept it. Students need to "develop and effectively apply critical thinking skills to their academic studies, to the complex problems that they will face, and to the critical choices they will be forced to make as a result of the information explosion and other rapid technological changes" (Oliver & Utermohlen, p. 1 ).
As mentioned in the section, Characteristics of Critical Thinking , critical thinking involves questioning. It is important to teach students how to ask good questions, to think critically, in order to continue the advancement of the very fields we are teaching. "Every field stays alive only to the extent that fresh questions are generated and taken seriously" (Center for Critical Thinking, 1996a ).
Beyer sees the teaching of critical thinking as important to the very state of our nation. He argues that to live successfully in a democracy, people must be able to think critically in order to make sound decisions about personal and civic affairs. If students learn to think critically, then they can use good thinking as the guide by which they live their lives.
Teaching Strategies to Help Promote Critical Thinking
The 1995, Volume 22, issue 1, of the journal, Teaching of Psychology , is devoted to the teaching critical thinking. Most of the strategies included in this section come from the various articles that compose this issue.
- CATS (Classroom Assessment Techniques): Angelo stresses the use of ongoing classroom assessment as a way to monitor and facilitate students' critical thinking. An example of a CAT is to ask students to write a "Minute Paper" responding to questions such as "What was the most important thing you learned in today's class? What question related to this session remains uppermost in your mind?" The teacher selects some of the papers and prepares responses for the next class meeting.
- Cooperative Learning Strategies: Cooper (1995) argues that putting students in group learning situations is the best way to foster critical thinking. "In properly structured cooperative learning environments, students perform more of the active, critical thinking with continuous support and feedback from other students and the teacher" (p. 8).
- Case Study /Discussion Method: McDade (1995) describes this method as the teacher presenting a case (or story) to the class without a conclusion. Using prepared questions, the teacher then leads students through a discussion, allowing students to construct a conclusion for the case.
- Using Questions: King (1995) identifies ways of using questions in the classroom:
- Reciprocal Peer Questioning: Following lecture, the teacher displays a list of question stems (such as, "What are the strengths and weaknesses of...). Students must write questions about the lecture material. In small groups, the students ask each other the questions. Then, the whole class discusses some of the questions from each small group.
- Reader's Questions: Require students to write questions on assigned reading and turn them in at the beginning of class. Select a few of the questions as the impetus for class discussion.
- Conference Style Learning: The teacher does not "teach" the class in the sense of lecturing. The teacher is a facilitator of a conference. Students must thoroughly read all required material before class. Assigned readings should be in the zone of proximal development. That is, readings should be able to be understood by students, but also challenging. The class consists of the students asking questions of each other and discussing these questions. The teacher does not remain passive, but rather, helps "direct and mold discussions by posing strategic questions and helping students build on each others' ideas" (Underwood & Wald, 1995, p. 18 ).
- Use Writing Assignments: Wade sees the use of writing as fundamental to developing critical thinking skills. "With written assignments, an instructor can encourage the development of dialectic reasoning by requiring students to argue both [or more] sides of an issue" (p. 24).
- Written dialogues: Give students written dialogues to analyze. In small groups, students must identify the different viewpoints of each participant in the dialogue. Must look for biases, presence or exclusion of important evidence, alternative interpretations, misstatement of facts, and errors in reasoning. Each group must decide which view is the most reasonable. After coming to a conclusion, each group acts out their dialogue and explains their analysis of it.
- Spontaneous Group Dialogue: One group of students are assigned roles to play in a discussion (such as leader, information giver, opinion seeker, and disagreer). Four observer groups are formed with the functions of determining what roles are being played by whom, identifying biases and errors in thinking, evaluating reasoning skills, and examining ethical implications of the content.
- Ambiguity: Strohm & Baukus advocate producing much ambiguity in the classroom. Don't give students clear cut material. Give them conflicting information that they must think their way through.
- Angelo, T. A. (1995). Beginning the dialogue: Thoughts on promoting critical thinking: Classroom assessment for critical thinking. Teaching of Psychology, 22(1), 6-7.
- Beyer, B. K. (1995). Critical thinking. Bloomington, IN: Phi Delta Kappa Educational Foundation.
- Center for Critical Thinking (1996a). The role of questions in thinking, teaching, and learning. [On-line]. Available HTTP: http://www.criticalthinking.org/University/univlibrary/library.nclk
- Center for Critical Thinking (1996b). Structures for student self-assessment. [On-line]. Available HTTP: http://www.criticalthinking.org/University/univclass/trc.nclk
- Center for Critical Thinking (1996c). Three definitions of critical thinking [On-line]. Available HTTP: http://www.criticalthinking.org/University/univlibrary/library.nclk
- Cooper, J. L. (1995). Cooperative learning and critical thinking. Teaching of Psychology, 22(1), 7-8.
- Jones, E. A. & Ratcliff, G. (1993). Critical thinking skills for college students. National Center on Postsecondary Teaching, Learning, and Assessment, University Park, PA. (Eric Document Reproduction Services No. ED 358 772)
- King, A. (1995). Designing the instructional process to enhance critical thinking across the curriculum: Inquiring minds really do want to know: Using questioning to teach critical thinking. Teaching of Psychology, 22 (1) , 13-17.
- McDade, S. A. (1995). Case study pedagogy to advance critical thinking. Teaching Psychology, 22(1), 9-10.
- Oliver, H. & Utermohlen, R. (1995). An innovative teaching strategy: Using critical thinking to give students a guide to the future.(Eric Document Reproduction Services No. 389 702)
- Robertson, J. F. & Rane-Szostak, D. (1996). Using dialogues to develop critical thinking skills: A practical approach. Journal of Adolescent & Adult Literacy, 39(7), 552-556.
- Scriven, M. & Paul, R. (1996). Defining critical thinking: A draft statement for the National Council for Excellence in Critical Thinking. [On-line]. Available HTTP: http://www.criticalthinking.org/University/univlibrary/library.nclk
- Strohm, S. M., & Baukus, R. A. (1995). Strategies for fostering critical thinking skills. Journalism and Mass Communication Educator, 50 (1), 55-62.
- Underwood, M. K., & Wald, R. L. (1995). Conference-style learning: A method for fostering critical thinking with heart. Teaching Psychology, 22(1), 17-21.
- Wade, C. (1995). Using writing to develop and assess critical thinking. Teaching of Psychology, 22(1), 24-28.
Other Reading
- Bean, J. C. (1996). Engaging ideas: The professor's guide to integrating writing, critical thinking, & active learning in the classroom. Jossey-Bass.
- Bernstein, D. A. (1995). A negotiation model for teaching critical thinking. Teaching of Psychology, 22(1), 22-24.
- Carlson, E. R. (1995). Evaluating the credibility of sources. A missing link in the teaching of critical thinking. Teaching of Psychology, 22(1), 39-41.
- Facione, P. A., Sanchez, C. A., Facione, N. C., & Gainen, J. (1995). The disposition toward critical thinking. The Journal of General Education, 44(1), 1-25.
- Halpern, D. F., & Nummedal, S. G. (1995). Closing thoughts about helping students improve how they think. Teaching of Psychology, 22(1), 82-83.
- Isbell, D. (1995). Teaching writing and research as inseparable: A faculty-librarian teaching team. Reference Services Review, 23(4), 51-62.
- Jones, J. M. & Safrit, R. D. (1994). Developing critical thinking skills in adult learners through innovative distance learning. Paper presented at the International Conference on the practice of adult education and social development. Jinan, China. (Eric Document Reproduction Services No. ED 373 159)
- Sanchez, M. A. (1995). Using critical-thinking principles as a guide to college-level instruction. Teaching of Psychology, 22(1), 72-74.
- Spicer, K. L. & Hanks, W. E. (1995). Multiple measures of critical thinking skills and predisposition in assessment of critical thinking. Paper presented at the annual meeting of the Speech Communication Association, San Antonio, TX. (Eric Document Reproduction Services No. ED 391 185)
- Terenzini, P. T., Springer, L., Pascarella, E. T., & Nora, A. (1995). Influences affecting the development of students' critical thinking skills. Research in Higher Education, 36(1), 23-39.
On the Internet
- Carr, K. S. (1990). How can we teach critical thinking. Eric Digest. [On-line]. Available HTTP: http://ericps.ed.uiuc.edu/eece/pubs/digests/1990/carr90.html
- The Center for Critical Thinking (1996). Home Page. Available HTTP: http://www.criticalthinking.org/University/
- Ennis, Bob (No date). Critical thinking. [On-line], April 4, 1997. Available HTTP: http://www.cof.orst.edu/cof/teach/for442/ct.htm
- Montclair State University (1995). Curriculum resource center. Critical thinking resources: An annotated bibliography. [On-line]. Available HTTP: http://www.montclair.edu/Pages/CRC/Bibliographies/CriticalThinking.html
- No author, No date. Critical Thinking is ... [On-line], April 4, 1997. Available HTTP: http://library.usask.ca/ustudy/critical/
- Sheridan, Marcia (No date). Internet education topics hotlink page. [On-line], April 4, 1997. Available HTTP: http://sun1.iusb.edu/~msherida/topics/critical.html
Walker Center for Teaching and Learning
- 433 Library
- Dept 4354
- 615 McCallie Ave
- 423-425-4188
The New York Times
The learning network | no quick fix developing problem-solving skills.

No Quick Fix? Developing Problem-Solving Skills

Academic Skills
Teaching ideas based on New York Times content.
- See all in Academic Skills »
- See all lesson plans »
Overview | How can real problems be approached and analyzed in ways that lead to practical solutions? What distinguishes effective solutions from ineffective ones? In this lesson, students consider how to work through a practical problem. They identify problems in their school that need fixing, then devise viable solutions to one of those problems, using problem-solving models and drawing on strategies like the social science of behavioral change. They then test some of their proposed solutions in the field and propose them to the school.
Materials | Computers with Internet access (optional); copies of the What’s Your Problem? handout (PDF)
Warm-Up | Tell students they will now consider a problem they recently confronted and make flow charts showing all the possible solutions they considered, including the final “fix.” You might explain that this exercise allows them to examine the critical thinking skills that they already use when looking for solutions to everyday problems.
To stimulate thinking, you might start by brainstorming some typical decisions, like when to do homework (modeled partly on the handout) or how to study for a challenging exam, or even relatively “light” problems, like what Halloween costume to wear.
Give students the What’s Your Problem? graphic organizer (PDF) to help them break down the various possible solutions and why each one did or did not work. You might also share some basic problem-solving steps to lead them in thinking through their problems.
Invite students to share their problems and solutions with the group and to reflect on the difference between solutions that seemed feasible but were not really effective in the long term. Invite students to reflect, too, on their thought process. Ask: What did you need to know about yourself and the task or problem in order to solve it successfully? What else did you need to know, about things like available resources, environment and so on? What is the difference between a quick fix and a successful solution?
Related | In the Op-Chart “Lunch Line Redesign,” Brian Wansink, David R. Just and Joe McKendry illustrate some tactics that have been used to influence children to make more healthful choices in the school cafeteria:
School cafeterias are much criticized for offering the kind of snack foods and desserts that contribute to childhood obesity. But banning junk food from cafeterias, as some schools have tried, or serving only escarole or tofu, can backfire. Students then skip lunch, bring in their own snacks or head out for fast food. We’ve even seen some pizzas delivered to a side door. Children and teenagers resist heavy-handed nutritional policies — and the food that is associated with the heavy hand. No food is nutritious, after all, until it is actually eaten. A smarter lunchroom wouldn’t be draconian. Rather, it would nudge students toward making better choices on their own by changing the way their options are presented. One school we have observed in upstate New York, for instance, tripled the number of salads students bought simply by moving the salad bar away from the wall and placing it in front of the cash registers.
Read the entire chart with your class, using the questions below.
Questions | For discussion and reading comprehension:
- How does food placement — both location and type of display — seem to affect the choices students make in the cafeteria?
- How do direct appeals, in the form of questions from cafeteria workers and descriptive text, seem to affect choice?
- How would you describe and categorize the other strategies?
- Why do you think these strategies resulted in more students buying more healthful foods?
- Which of these tactics do you think might work in our own cafeteria? Why?
RELATED RESOURCES
From the learning network.
- Lesson: Smart Design
- Lesson: Mind Your Own Business
- Lesson: Experience Innovation
From NYTimes.com
- Freakonomics: Our Love/Hate Relationship With Carrots and Sticks
- Taking Lessons From What Went Wrong
- School’s New Rule for Pupils in Trouble: No Fun
Around the Web
- Invention Convention
- How to Solve It by George Polya
- Invention Highway
Activity | Explain to students that they will now brainstorm problems in the school, then choose one to try to solve.
Encourage students to think in categories. Here are some categories to get you started, along with an example of a specific topic for each one:
- Technology; cellphones as learning tools
- Design ; desks and workstations
- Resource management ; energy efficiency
- Use of classrooms and public spaces; overcrowding
- Environmentalism; recycling
- Health and hygiene; hand sanitizers
- School culture; bullying and cyberbullying
Make sure students narrow categories and topics down to specific problems. For example, for overcrowding, they might focus on the question of how to ease hallway congestion during passing times. Students might also expand beyond strictly school-based problems to include school-related problems, like chronic lack of sleep among students.
After brainstorming is over, have the class vote on one problem to tackle as a group. Then put students in working groups of pairs or trios to identify, research and propose a viable and innovative solution for the problem.
You may wish to first familiarize students with the four-step problem-solving method of the mathematician George Polya . Have students approach their problem using the following steps, which apply Polya’s method:
Step 1: Understand the Problem — Formulate a clear statement of the desired outcome of the problem by asking the questions: What do we know about the problem? What do we not know? Is there enough information to help us find a solution? If not, what information do we need?
Step 2: Collect Data — Go out into the field to make observations and collect data that will help us better understand the problem and identify its most significant factors. For example, if students are trying to solve the problem of hallway overcrowding, they might post students in various places to observe traffic and congestion spots at different times of day (analogies to car traffic jams might be useful), interview teachers, students, administrators and school employees, and collect data like hallway width, number of total students, number of students coming out of classrooms and time between classes. (Groups might collaborate on this step to avoid redundancies.)
Step 3: Devise a Plan — With data in hand, working groups discuss and brainstorm possible solutions, using the What’s Your Problem? graphic organizer (PDF).
Students might consider using one of the following innovative problem-solving methods:
- Crowdsourcing , which uses social networks and collaboration to find possible solutions to problems that include improving software and improving education .
- Behavioral change , which uses social science and various behavior change theories , along with related strategies like the use of design and tools like commitment contracts to influence behavior.
- Positive deviance , an unorthodox approach to problem solving that focuses on what some people do right rather than what most people do wrong.
For further inspiration, they might look at the annual Year in Ideas issues of The Times Magazine from 2009 , 2008 and earlier .
For each potential solution to their real-world problems , students discuss reasons that it may or may not work. In the instance of overcrowded hallways, for example, students might propose increasing passing time, encouraging students to put large bags into lockers or mandating traffic routes.
Carry Out the Plan — Each group takes on one solution to develop further and, if possible, tests it either in the field or even through role playing .
Going Further | Students share their ideas, then discuss and vote on the solutions. Which is most innovative? Which is most practical? Which do they expect to be most effective, and why? Which one deserves to be tried first?
They pitch their solution, or a grab bag of solutions, by starting a public service announcement campaign , writing letters to the editor of the school paper or giving a presentation to the school administration or PTA.
Alternatively or additionally, to have students undertake a larger issue, they might read up on social entrepreneurship , including Nicholas Kristof’s Times Magazine article “D.I.Y. Foreign-Aid Revolution” and his related blog post, “How to Change the World.” They can also follow the new Fixes blog, which “explores solutions to major social problems” and “examines creative initiatives that can tell us about the difference between success and failure.”
Standards | This lesson is correlated to McREL’s national standards (it can also be aligned to the new Common Core State Standards ):
Life Skills: Thinking and Reasoning 1. Understands and applies the basic principles of presenting an argument 2. Understands and applies basic principles of logic and reasoning 3. Effectively uses mental processes that are based on identifying similarities and differences 4. Understands and applies basic principles of hypothesis testing and scientific inquiry 5. Applies basic troubleshooting and problem-solving techniques 6. Applies decision-making techniques
Life Skills: Life Work 6. Makes effective use of basic life skills
Life Skills: Working With Others 1. Contributes to the overall effort of a group 4. Displays effective interpersonal communication skills
Behavioral Studies 1. Understands that group and cultural influences contribute to human development, identity and behavior 2. Understands various meanings of social group, general implications of group membership, and different ways that groups function 3. Understands that interactions among learning, inheritance and physical development affect human behavior 4. Understands conflict, cooperation and interdependence among individuals, groups and institutions
Family/Consumer Sciences 4. Understand how knowledge and skills related to consumer and resources management affect the well-being of individuals, families and society
Economics 1. Understands that scarcity of productive resources requires choices that generate opportunity costs
Language Arts 4. Gathers and uses information for research purposes 8. Uses listening and speaking strategies for different purposes
Comments are no longer being accepted.
Educational
Before finding solutions of a problem, the reason for the existence of the problem should be examined and understood. When searching for the “reason of reasons” of a problem (using a fishbone diagram for example) the result is a solution that not only takes care of the problem, but may improve the whole process that was the origin of the problem.
This is a great resource for problem-solving lesson material. The cafeteria Op-chart is a perfect example of strategic thinking in action and the school setting makes it very transferable to students. With that as an example – students can go on to solve other real-world problems.
I’ve been a long-time proponent of rigor, relevance and project based learning. Two good places for readers to start are these problem solving lessons:
“First Day of School? Don’t Pass Out Books – Problem Solve.” //bit.ly/9eS0l
“Why Don’t We Teach Sequencing Skills? It’s an Essential Higher-Order Thinking Strategy” //bit.ly/142djQ
Teachers will find a variety of teaching plans under my “strategy” category //peterpappas.blogs.com/copy_paste/strategies/
Very good work. In fact I am now using this content as my base for training my student teachers (I am a teacher educator) the steps and pedagogy of Action Research, and this topic shall form as an example. Good job… and thanks
Planning is very important in each step of career development. Students will do well in education and career in which they are interested; hence choosing the right education is very important. It is not possible to achieve “Excellence in education” if you are in a education towards which you are not seriously inclined. Hence people advocate choosing a education and profession based on your passion.
What's Next
Unit 7B: Thinking, Problem Solving, Creativity, and Language
UNIT PREVIEW
Concepts, the building blocks of thinking, simplify the world by organizing it into a hierarchy of categories. Concepts are often formed around prototypes, or the best examples of a category.
When faced with a novel situation for which no well-learned response will do, we may use problem-solving strategies such as trial and error, algorithms, heuristics, and insight. Creative people solve problems but in novel and valuable ways. Obstacles to successful problem solving include the confirmation bias, mental set, and functional fixedness. Heuristics provide efficient, but occasionally misleading, guides for making quick decisions. Overconfidence, belief perseverance, and framing further reveal our capacity for error. Still, human cognition is remarkably efficient and adaptive. With experience, we grow adept at making quick, shrewd judgments.
Language facilitates and expresses our thoughts. Spoken language is built from phonemes, morphemes, words, and the semantics and syntax that make up grammar. The ease with which children master language has sparked a lively debate over whether children acquire language through association and imitation or are biologically prepared to learn words and use grammar.
Thinking and language are difficult to separate. Although the linguistic determinism hypothesis states that language determines thought, we know that thinking can occur without language, that we often think in images, and so we might better say that thinking affects our language, which then affects our thoughts.
Click on link below for a Crash Course on Cognition:
Cognition refers to the mental activities associated with thinking, knowing, remembering, and communicating. Cognitive psychologists study these activities including the logical and illogical ways we create concepts, solve problems, make decisions, and form judgments.
To think about the countless events, objects, and people in our world, we organize them into mental groupings called concepts . To simplify things further, we organize concepts into category hierarchies . Although we form some concepts by definition—for example, a triangle has three sides— more often we form a concept by developing a prototype , a mental image or best example of a particular category. For example, a robin more closely resembles our “bird” category than does a penguin. The more closely objects match our prototype of a concept, the more readily we recognize them as examples of a concept. Once we place an item in a category, our memory of it later moves in the direction of the category prototype.
We approach some problems through trial and error, attempting various solutions until stumbling upon one that works. For other problems, we may follow a methodical rule or step-by-step procedure called an algorithm. Because algorithms can be laborious, we often rely instead on simple thinking strategies called heuristics . Speedier than algorithms, heuristics are also more errorprone. Sometimes, however, we are unaware of using any problem-solving strategy; the answer just comes to us as a sudden flash of insight . Researchers have identified brain activity associated with insight .
In general, a certain level of aptitude is necessary but not sufficient for creativity (the ability to produce novel and valuable ideas). Studies suggest five other components of creativity: expertise, imaginative thinking skills, a venturesome personality, intrinsic motivation, and a creative environment. The brain regions supporting the convergent thinking tested by intelligence tests (requiring a single correct answer) differ from those supporting the divergent thinking that imagines multiple solutions to a problem (such as how many uses you can think of for a brick).
Another obstacle to problem solving is fixation —the inability to see a problem from a fresh perspective. The tendency to repeat solutions that have worked in the past is a type of fixation called mental set . It may interfere with our taking a fresh approach when faced with problems that demand an entirely new solution. Our tendency to perceive the functions of objects as fixed and unchanging is called functional fixedness . Perceiving and relating familiar things in new ways is an important aspect of creativity.
The representativeness heuristic involves judging the likelihood of things in terms of how well they seem to represent, or match, particular prototypes. If something matches our mental representation of a category, that fact usually overrides other considerations of statistics or logic. The availability heuristic operates when we base our judgments on the availability of information in our memories. If instances of an event come to mind readily, perhaps because of their vividness, we presume such events are common. Both heuristics enable us to make snap judgments. However, these quick decisions sometimes lead us to ignore important information or to underestimate the chances of something happening. Overconfidence , the tendency to overestimate the accuracy of our knowledge and judgments, can have adaptive value. People who err on the side of overconfidence live more happily, find it easier to make tough decisions, and seem more credible than those who lack self-confidence. At the same time, failing to appreciate one’s potential for error when making military, economic, or political judgments can have devastating consequences.
We exhibit belief perseverance , clinging to our ideas in the face of contrary evidence, because the explanation we accepted as valid lingers in our minds. Once beliefs are formed and justified, it takes more compelling evidence to change them than it did to create them. The best remedy for this form of bias is to make a deliberate effort to consider evidence supporting the opposite position. Although human intuition is sometimes perilous, it can be, whether conscious or unconscious, remarkably efficient and adaptive. Moreover, it feeds our expertise, our creativity, our love, and our spirituality. Smart intuition is born of experience. As we gain expertise in a field, we become better at making quick, adept judgments. Experienced nurses, firefighters, art critics, hockey players, and anyone who develops a deep and special knowledge learn to size up a situation in an eyeblink. Intuition is powerful, but sometimes perilous, and especially so when we overfeel and underthink, as we do when judging risks. So, we need to check our intuitions against reality. The same issue presented in two different but logically equivalent ways can elicit quite different answers. This framing effect suggests that our judgments and decisions may not be well reasoned and that those who understand the power of framing can use it to influence important decisions— for example, by wording survey questions to support or reject a particular viewpoint.
Click on link below for a Crash Course lesson on Language:
Language is our way of combining words to communicate meaning. Spoken language is built from basic speech sounds, called phonemes ; elementary units of meaning, called morphemes ; and words. Finally, language must have a grammar , a system of rules that enables us to communicate with and understand others. Semantics refers to the rules we use to derive meaning from the morphemes, words, and sentences; syntax refers to the rules we use to order words into grammatically sensible sentences. In all 6000 human languages, the grammar is intricately complex.
Children’s language development moves from simplicity to complexity. Their receptive language abilities mature before their productive language . Beginning at about 4 months, infants enter a babbling stage in which they spontaneously utter various sounds at first unrelated to the household language. By about age 10 months, a trained ear can identify the language of the household by listening to an infant’s babbling. Around the first birthday, most children enter the one-word stage , and by their second birthday, they are uttering two-word sentences . This two-word stage is characterized by telegraphic speech . This soon leads to their uttering longer phrases (there seems to be no “three-word stage”), and by early elementary school, they understand complex sentences.
The debate between the behaviorist view that emphasizes learning and the view that each organism comes with innate predispositions surfaces again in theories of language development. Representing the nurture side of the argument, behaviorist B. F. Skinner argued that we learn language by the familiar principles of association (of sights of things with sounds of words), imitation (of words and syntax modeled by others), and reinforcement (with success, smiles, and hugs after saying something right). Challenging this claim, and representing the nature side of the debate, Noam Chomsky notes that children are biologically prepared to learn words and use grammar (they are born with what Chomsky called a language acquisition device already in place). He argues that children acquire untaught words and grammar at too fast a rate to be explained solely by learning principles. Moreover, there is a universal grammar that underlies all human language. Cognitive neuroscientists suggest that the statistical analysis that children perform during life’s first years is critical for the mastery of grammar. Skinner’s emphasis on learning helps explain how infants acquire their language as they interact with others. Chomsky’s emphasis on our builtin readiness to learn grammar helps explain why preschoolers acquire language so readily and use grammar so well. Nature and nurture work together. Childhood does seem to represent a critical (or “sensitive”) period for certain aspects of learning. Research indicates that children who have not been exposed to either a spoken or signed language by about age 7 gradually lose their ability to master any language. Learning a second language also becomes more difficult after the window of opportunity closes. For example, adults who attempt to master a second language typically speak it with the accent of their first.
Thinking and Language
Although Benjamin Whorf’s linguistic determinism hypothesis suggests that language determines thought, it is more accurate to say that language influences thought. Language expresses our thoughts, and different languages can embody different ways of thinking. Many bilinguals report that they have a different sense of self, depending on which language they use. We use language in forming categories, and words can influence our thinking about colors. Perceived differences grow when we assign different names to colors. Given the subtle influence of words on thinking, we ought to choose our words carefully. Studies of the effects of the generic pronoun he and the ability of vocabulary enrichment to enhance thinking reveal the influence of words. We might say that our thinking influences our language, which then affects our thoughts.
We often think in images. In remembering how we do things, for example, turning on the water in the bathroom, we use nondeclarative (procedural) memory—a mental picture of how we do it. Artists, composers, poets, mathematicians, athletes, and scientists all find images to be helpful. Researchers have found that thinking in images is especially useful for mentally practicing upcoming events and can actually increase our skills. Research suggests that mental rehearsal can help one to achieve an academic goal.
Varstiy Tutor Flashcards:
https://www.varsitytutors.com/ap_psychology-flashcards/conscious-thought-and-problem-solving
https://www.varsitytutors.com/ap_psychology-flashcards/language
*Work Cited: All summary notes come from *Myers Pyschology for AP, Lecture Guides (2011 Worth Publishers)

IMAGES
VIDEO
COMMENTS
A problem solving strategy guaranteed to produce a solution even if the user does not know how it works. A rule of thumb that suggests a course of action or guides problem solving but does not guarantee an optimal solution. The drawing of conclusions or inferences from observations, facts, or assumptions.
Reflection and Self-Regulation. G. The two main components of metacognition. Metacognition. E. Can be defined as thinking about thinking. Gestalt Theory. C. Theory that the whole is greater than the sum of its parts. Study with Quizlet and memorize flashcards containing terms like Convergent Thinking, Divergent Thinking, Concept and more.
A new mental arrangement of the same elements. What is the definition of Insight? The sudden emergence of a solution by the recombination of elements. Study with Quizlet and memorize flashcards containing terms like What is the definition of Thinking?, What is the definition of Prototype?, What is the definition of a Rule? and more.
Algorithms, heuristics, and the role of confirmation bias (7.3) Effective problem-solving sequence (7.3) Apply. By reading and thinking about how the concepts in Module 7 apply to real life, you should be able to: Identify which type of knowledge a piece of information is (7.1) Recognize examples of deductive and inductive reasoning (7.2)
The simple sudoku below ( Figure 7.7) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column.
SUMMARY. The process of knowing or acquiring knowledge is called cognition. The process of acquiring knowledge is facilitated by cognitive processes such as attention, thinking, remembering, and reasoning. The cognitive processes are very much specific to human beings and are guided by concepts, facts, propositions, rules, and memories.
Using Critical Thinking Skills in Problem Solving. Think of problem solving as a process with four Ps: Define the problem, generate possibilities, create a plan, and perform your plan. Step 1: Define the problem. To define a problem effectively, understand what a problem is—a mismatch between what you want and what you have.
7.1 What Thinking Means; 7.2 Creative Thinking; 7.3 Analytical Thinking; 7.4 Critical Thinking; 7.5 Problem-Solving; 7.6 Metacognition; 7.7 Information Literacy; Career Connection; Rethinking; Where do you go from here?
Unit 7 Lesson 8 Problem Solving with Fractions Question 4. Bert used \(\frac{7}{8}\) foot of an oak board to make a tray. Akio made his tray from \(\frac{4}{4}\) foot of the same oak board. ... Stretch Your Thinking Christine and Alan each buy the same size sandwich. Christine eats \(\frac{3}{4}\) of her sandwich. Alan eats more of his sandwich ...
INTEXT QUESTIONS 7.2 1. Define problem solving. Discuss the two types of problem solving. _____ 2. Discuss the role of mental set in problem solving. _____ 7.3 CREATIVITY AND ITS ROLE IN LIFE Do you know whatever you see around you, the things which you use for work in everyday life, the transport you use for commuting from one place to another ...
Lesson Two Problem Solving Activity 2.1: Tower of Hanoi and Chess Activity 2.2: Video Games and Problem Solving Critical Thinking Exercise 2.1: Talk Through an Everyday Problem Critical Thinking Exercise 2.2: Problems and Riddles Activity 2.3: Compound Remote Associates Problems Activity 2.4: Divergent Thinking with the Alternative Uses Task
critical thinking. Study with Quizlet and memorize flashcards containing terms like 1. Finding common elements in different situations 2. Using general rules to solve individual problems 3. Making an educated guess based on current information, 1. Estimating the length of a room without a yardstick 2. Updating a computer with new software 3.
11.2.2 Barriers to Problem Solving Mental set-When you solve a problem in a one particular way, it becomes a set. These are already tried mental operations or steps. This could lead to success in some situation but could also create a kind of mental rigidity that acts as a hindrance to think in new ways, rules and strategies for problem solving.
This is only one facet of the complex processes involved in cognition. Simply put, cognition is thinking, and it encompasses the processes associated with perception, knowledge, problem solving, judgment, language, and memory. Scientists who study cognition are searching for ways to understand how we integrate, organize, and utilize our ...
This problem-solving technique requires you to move beyond your comfort zone and consider a problem from a range of different perspectives by essentially wearing different thinking hats. Humans are creatures of habit; if someone is an emotional thinker, they will have a tendency to approach every problem with this mindset, resulting in similar ...
Critical thinking involves asking questions, defining a problem, examining evidence, analyzing assumptions and biases, avoiding emotional reasoning, avoiding oversimplification, considering other interpretations, and tolerating ambiguity. Dealing with ambiguity is also seen by Strohm & Baukus (1995) as an essential part of critical thinking ...
Sensory Memory. Sensory memory refers to the instantaneous recording of information as it enters one of the five sensory systems. The information is kept for only a few seconds or less. There are systems related to all five senses, including sight, sound, smell, touch, and taste. Visual systems involve iconic memory.
Understands and applies basic principles of logic and reasoning. 3. Effectively uses mental processes that are based on identifying similarities and differences. 4. Understands and applies basic principles of hypothesis testing and scientific inquiry. 5. Applies basic troubleshooting and problem-solving techniques. 6.
Unit 7B: Thinking, Problem Solving, Creativity, and Language. UNIT PREVIEW. Concepts, the building blocks of thinking, simplify the world by organizing it into a hierarchy of categories. Concepts are often formed around prototypes, or the best examples of a category. When faced with a novel situation for which no well-learned response will do ...
Unit 3 Psychology - Learning, Memory, & Problem Solving. Get a hint. Classical Conditioning. Click the card to flip 👆. A learning procedure in which associations are made between a natural stimulus and a learned, neutral stimulus. Click the card to flip 👆. 1 / 24.
Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below ( Figure 7.7) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column.
Module 7.1 Thinking. Define thinking. Describe several ways in which we represent information in our minds. Explain the difference between logical and natural concepts. Identify and describe mental strategies we can use to solve problems more effectively. Identify and describe mental roadblocks that impede problem solving and decision making ...
AP Psych Unit 7: Cognition: 7B—Thinking, Problem Solving, Creativity, and Language. Flashcards. Learn. Test. Match. cognition. ... method of problem solving (Thomas Edison tried thousands of light bulb filaments before stumbling upon one that worked) algorithm. a methodical, logical rule or procedure that guarantees solving a particular ...